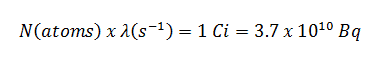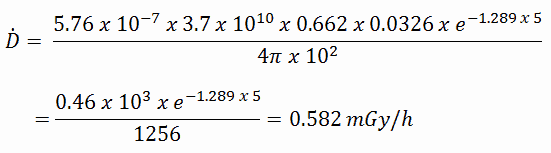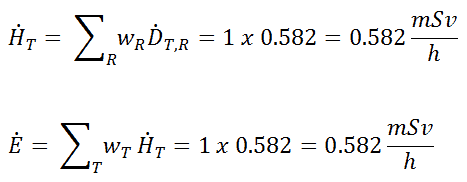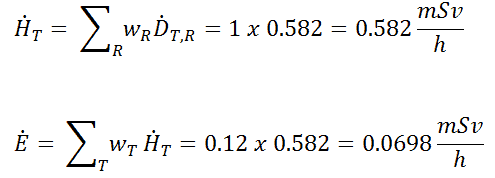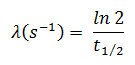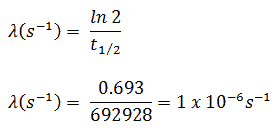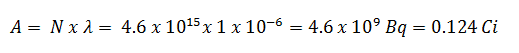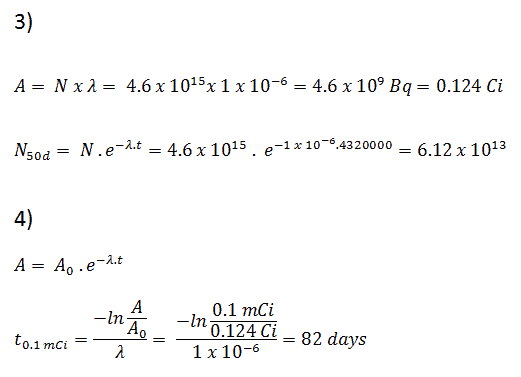Nick Connor, Author at Radiation Dosimetry

Was ist die Abschirmung gegen ionisierende Strahlung – Definition

Juli 10, 2021Juli 11, 2020 von Nick Connor

Die Abschirungen gegen ionisierende Strahlung dienen zum Schutz von Personen (s. Strahlenschutz), anderen Lebewesen, Gegenständen oder Bauteilen gegen Strahlenschaden, sowie zur Reduktion des Hintergrunds bei Strahlenmessungen.

Strahlenschutz ist die Wissenschaft und Praxis des Schutzes von Mensch und Umwelt vor den schädlichen Auswirkungen ionisierender Strahlung. Es ist ein ernstes Thema nicht nur in Kernkraftwerken , sondern auch in der Industrie oder in medizinischen Zentren. Beim Strahlenschutz gibt es drei Möglichkeiten, Menschen vor identifizierten Strahlenquellen zu schützen:

Aufenthalt. Die Höhe der Strahlenexposition hängt direkt (linear) von der Zeit ab, die Menschen in der Nähe der Strahlungsquelle verbringen. Die Dosis kann durch Begrenzung der Expositionszeit reduziert werden .
Abstand. Die Höhe der Strahlenexposition hängt von dem Abstand von der Strahlung ab. Ähnlich wie bei einer Hitze von einem Feuer ist die Intensität der Wärmestrahlung hoch, wenn Sie zu nahe sind, und Sie können sich verbrennen. Wenn Sie in der richtigen Entfernung sind, können Sie dort problemlos standhalten und es ist außerdem bequem. Wenn Sie zu weit von der Wärmequelle entfernt sind, kann Sie auch die Unzulänglichkeit der Wärme verletzen. Diese Analogie kann in gewissem Sinne auch auf Strahlung von Strahlungsquellen angewendet werden.
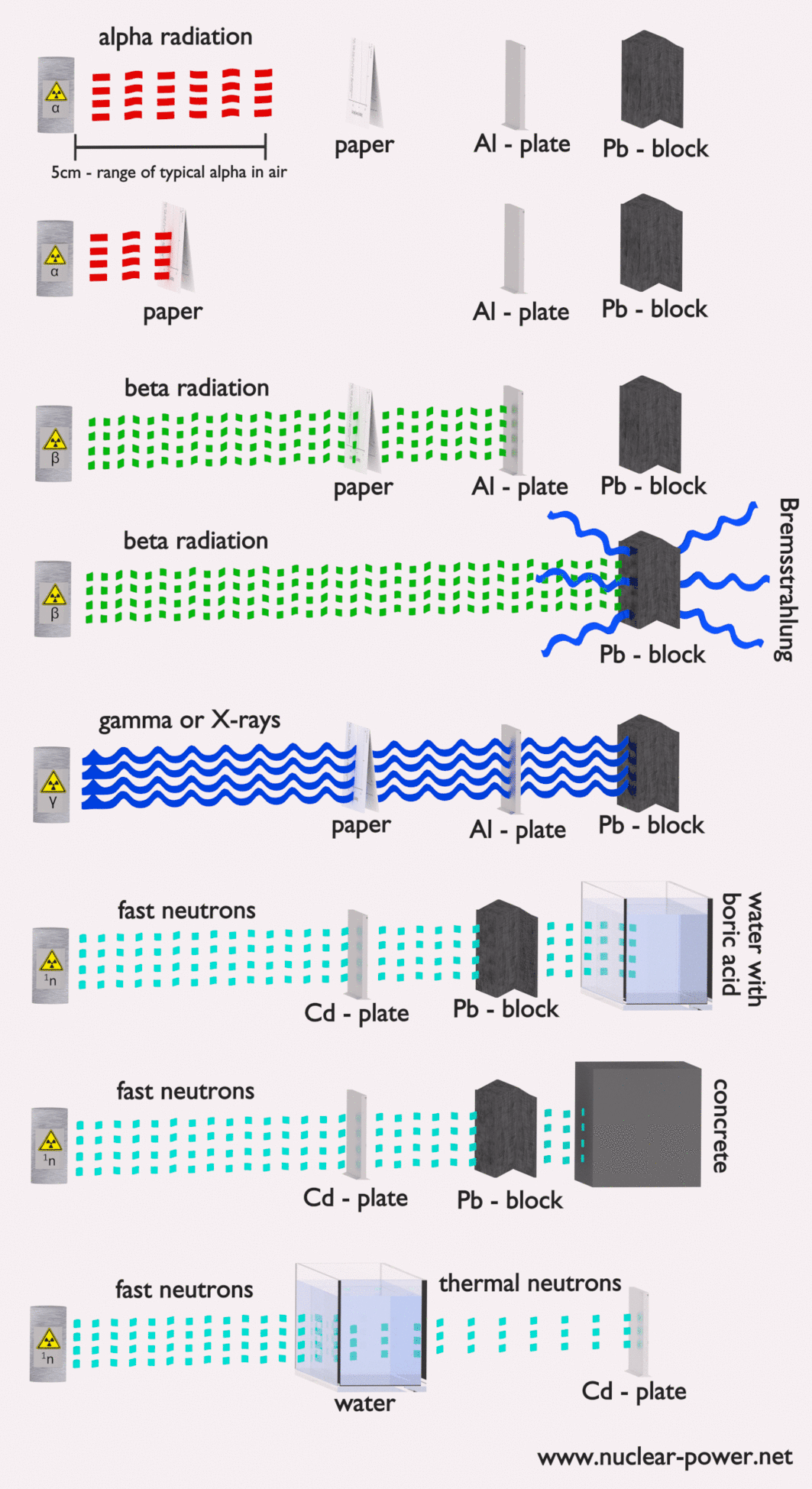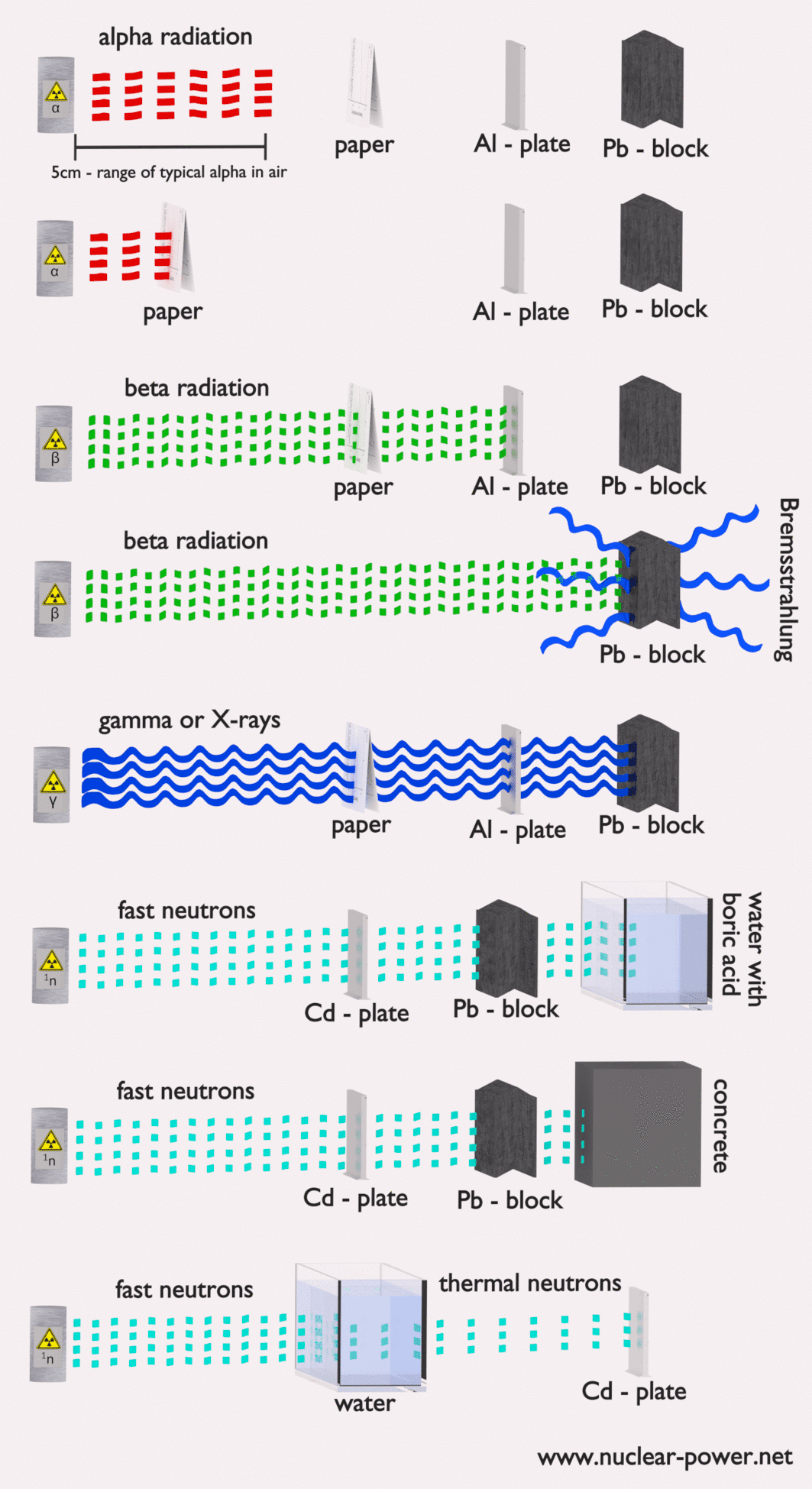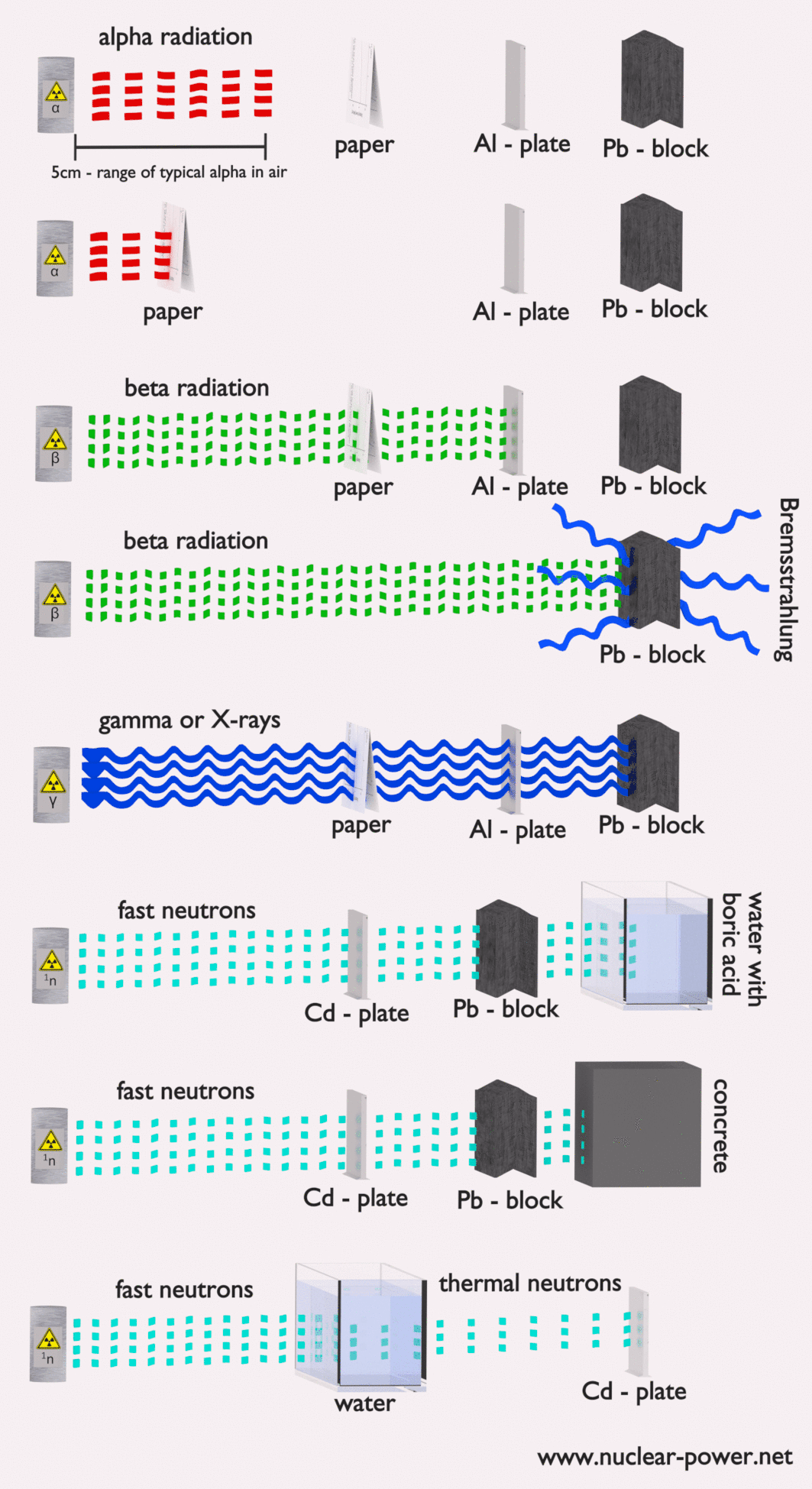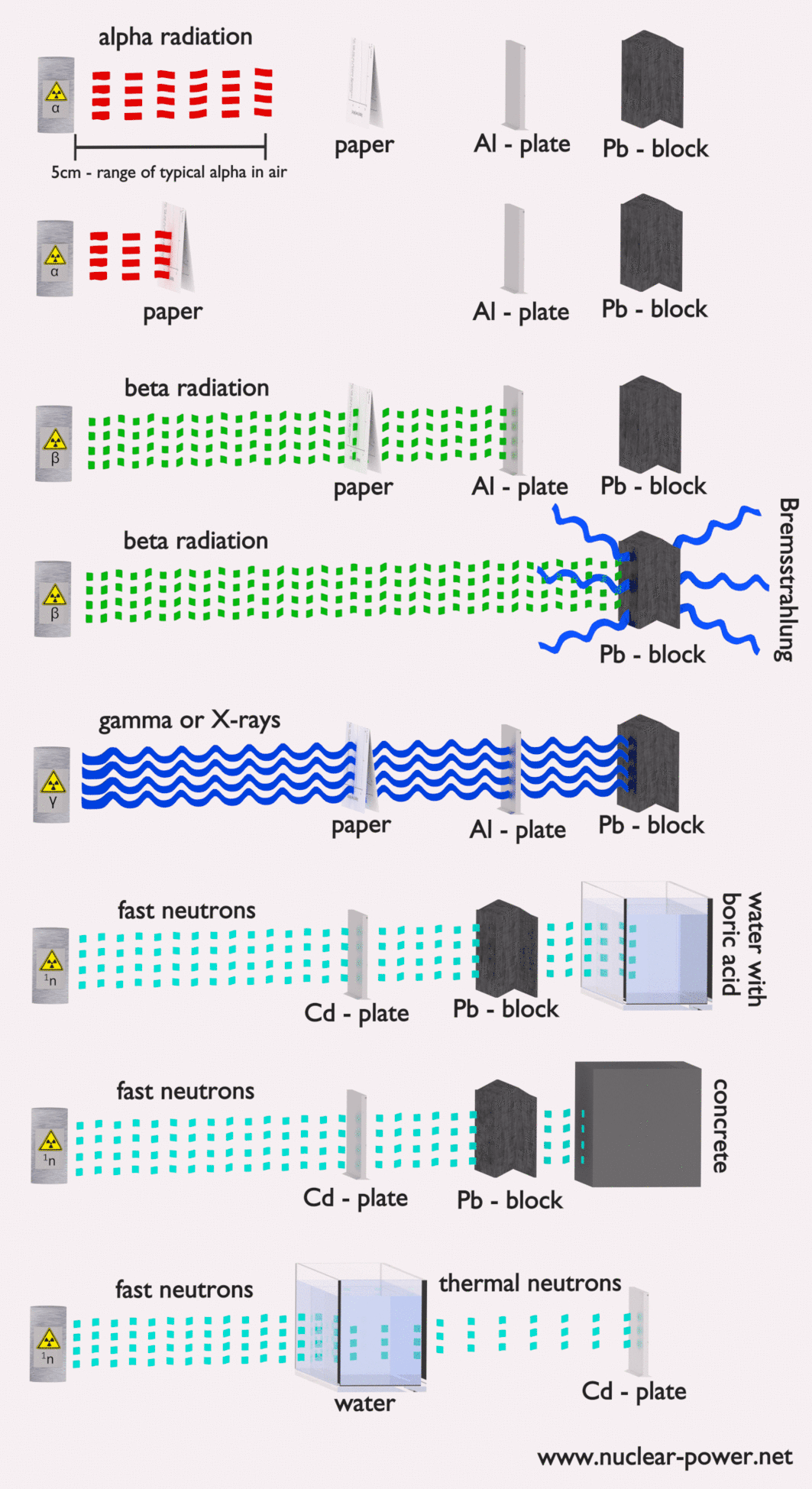
Abschirmung. Wenn die Quelle zu intensiv ist und Zeit oder Entfernung keinen ausreichenden Strahlenschutz bieten, muss die Abschirmung verwendet werden. Strahlenschutz besteht normalerweise aus Barrieren aus Blei, Beton oder Wasser. Es gibt viele verschiedene Materialien, die zur Strahlenabschirmung verwendet werden können, aber es gibt viele verschiedene Situationen beim Strahlenschutz. Dies hängt stark von der Art der abzuschirmenden Strahlung, ihrer Energie und vielen anderen Parametern ab. Zum Beispiel kann sogar abgereichertes Uran als guter Schutz vor Gammastrahlung verwendet werden, andererseits ist Uran eine absolut ungeeignete Abschirmung von Neutronenstrahlung.

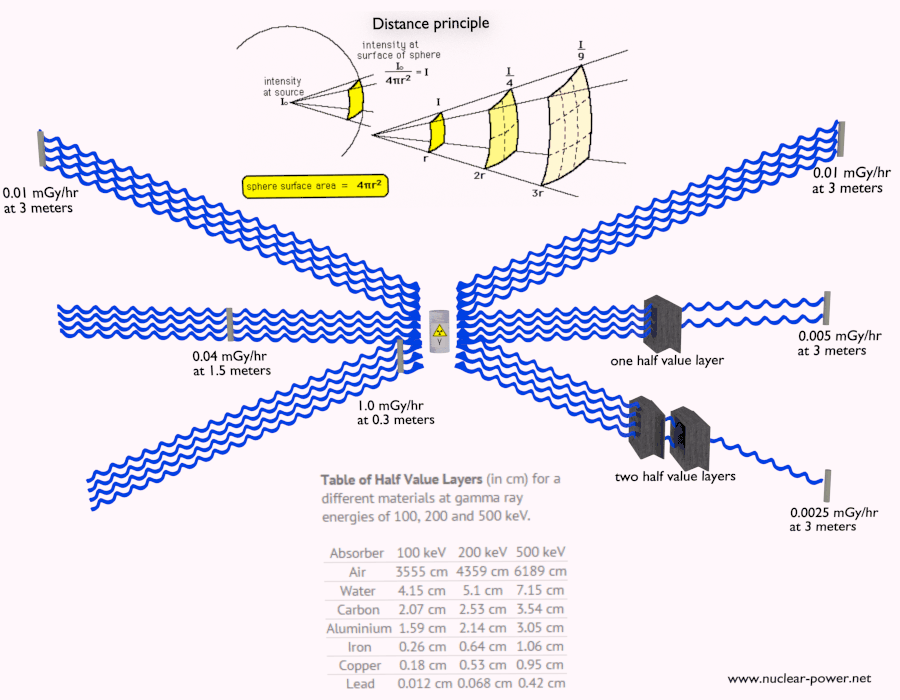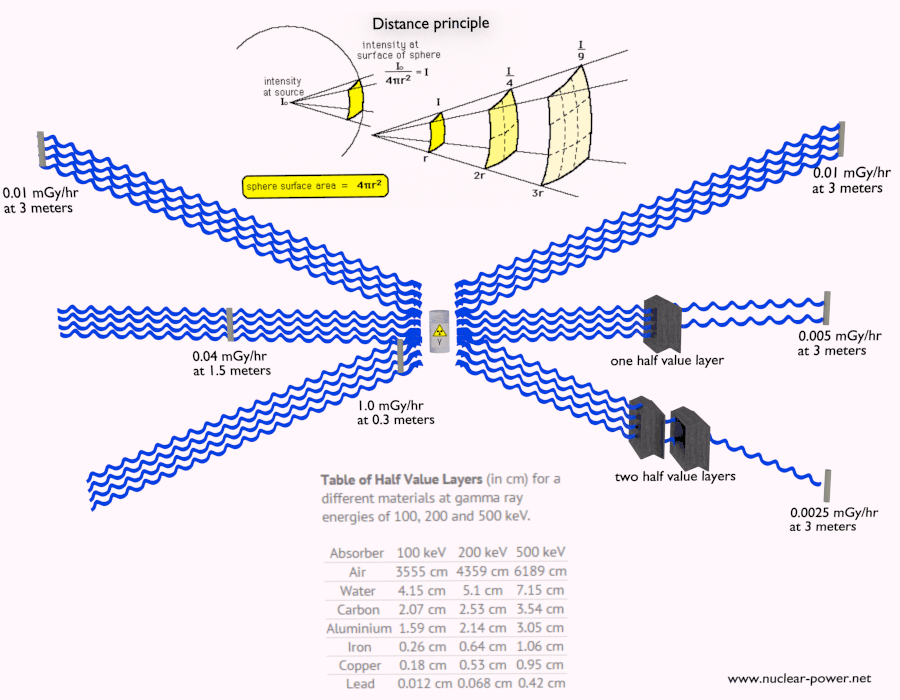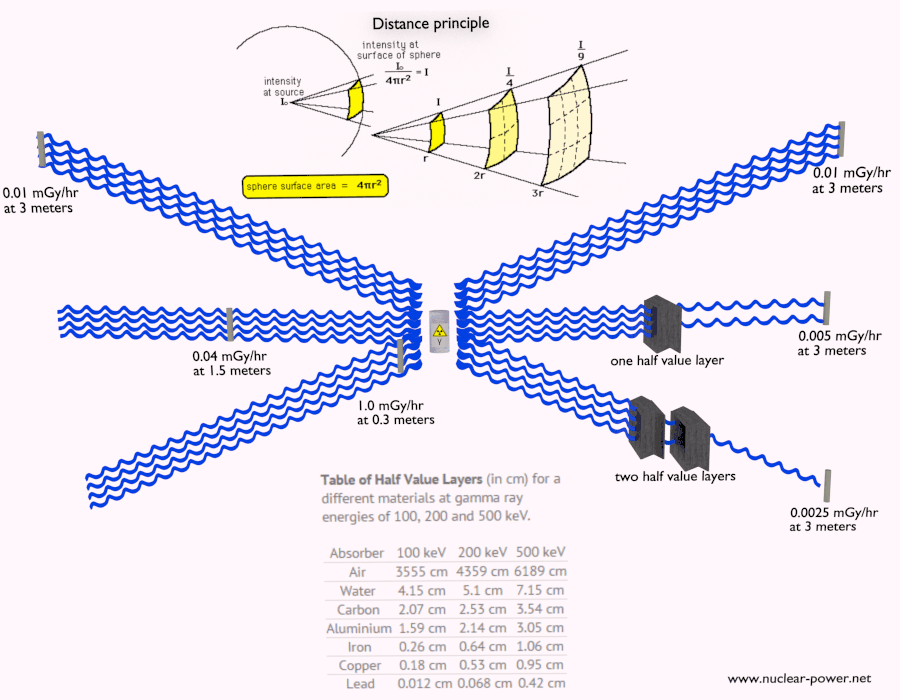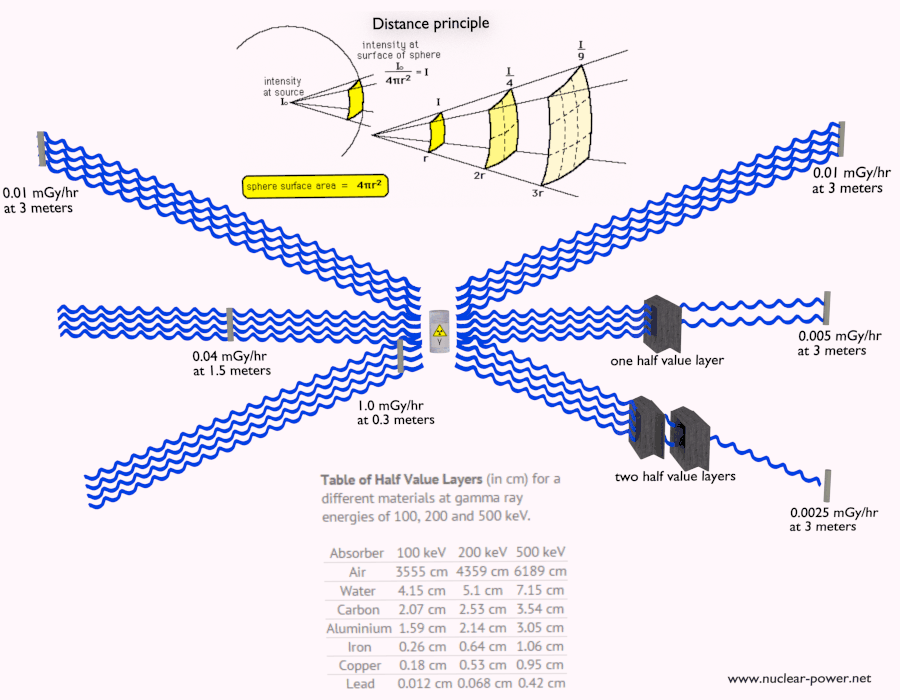
Strahlenschutzprinzipien - Zeit, Entfernung, Abschirmung — Prinzipien des Strahlenschutzes – Zeit, Entfernung, Abschirmung

Strahlenschutz bedeutet einfach, dass sich zwischen der Strahlungsquelle und Ihnen (oder einem Gerät) Material befindet , das die Strahlung absorbiert . Das Ausmaß der erforderlichen Abschirmung, die Art oder das Material der Abschirmung hängen stark von mehreren Faktoren ab. Wir sprechen nicht über eine Optimierung.In einigen Fällen kann eine unangemessene Abschirmung sogar die Strahlungssituation verschlechtern, anstatt Menschen vor der ionisierenden Strahlung zu schützen. Grundlegende Faktoren, die beim Vorschlag einer Strahlenabschirmung berücksichtigt werden müssen, sind:

Art der abzuschirmenden ionisierenden Strahlung
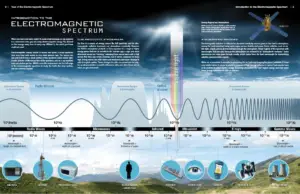
Energiespektrum der ionisierenden Strahlung
Expositionsdauer
Abstand von der Quelle der ionisierenden Strahlung
Anforderungen an die Dämpfung der ionisierenden Strahlung – ALARA- oder ALARP-Prinzipien
Gestaltungsfreiheitsgrad
Andere physikalische Anforderungen (z. B. Transparenz bei Bleiglasschirmen)

Siehe auch: Wechselwirkung von Strahlung mit Materie

Siehe auch: Rad Pro Calculator

Abschirmung der Strahlung in Kernkraftwerken

Im Allgemeinen hat die Strahlenabschirmung in der Nuklearindustrie viele Zwecke. In Kernkraftwerken besteht der Hauptzweck darin, die Strahlenexposition von Personen und Personal in der Nähe von Strahlungsquellen zu verringern . In KKW ist die Hauptstrahlungsquelle eindeutig der Kernreaktor und sein Reaktorkern . Kernreaktoren sind im Allgemeinen leistungsstarke Quellen für das gesamte Spektrum ionisierender Strahlung . Die zu diesem Zweck verwendete Abschirmung wird als biologische Abschirmung bezeichnet .

Dies ist jedoch nicht der einzige Zweck der Strahlenabschirmung. In einigen Reaktoren werden auch Schilde verwendet, um die Intensität der auf das Reaktorgefäß einfallenden Gammastrahlen oder Neutronen zu verringern . Diese Strahlungsabschirmung schützt den Reaktorbehälter und seine Einbauten ( zum Beispiel der Kernträger barrel ) aus der übermäßigen Erwärmung aufgrund der Gammastrahlenabsorption schneller Neutronenmoderation . Solche Abschirmungen werden üblicherweise als thermische Abschirmungen bezeichnet .

Siehe auch: Neutronenreflektor

Ein wenig seltsamer Strahlenschutz wird normalerweise verwendet, um das Material des Reaktordruckbehälters zu schützen (insbesondere in PWR-Kraftwerken ). Strukturmaterialien von Druckbehälter- und Reaktorinnenteilen werden insbesondere durch schnelle Neutronen beschädigt . Schnelle Neutronen erzeugen strukturelle Defekte, die zu Versprödung des Druckbehältermaterials führen . Um den Neutronenfluss an der Gefäßwand zu minimieren, kann auch die Kernladestrategie modifiziert werden. Bei der „Out-In“ -Kraftstoffladestrategie werden frische Brennelemente am Rand des Kerns platziert. Diese Konfiguration verursacht eine hohe Neutronenfluenz an der Gefäßwand. Daher die Kraftstoffeinladestrategie „In-Out“ (mit geringen Leckagemustern – L3P) wurde in vielen Kernkraftwerken übernommen. Im Gegensatz zur „Out-In“ -Strategie weisen Kerne mit geringer Leckage in der zweiten Reihe frische Brennelemente auf, nicht am Umfang des Kerns. Die Peripherie enthält Kraftstoff mit höherem Kraftstoffverbrauch und geringerer relativer Leistung und dient als hochentwickelter Strahlungsschutz.

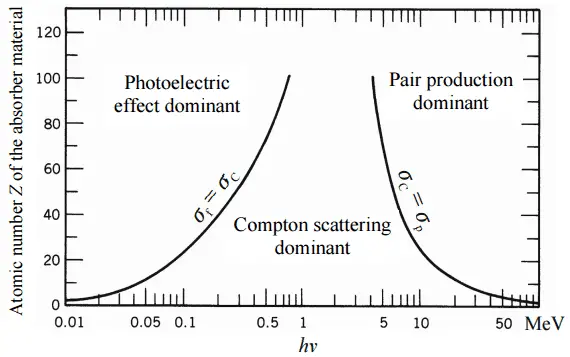
In Kernkraftwerken besteht das zentrale Problem darin, sich gegen Gammastrahlen und Neutronen abzuschirmen , da die Bereiche geladener Teilchen (wie Beta-Teilchen und Alpha-Teilchen) in der Materie sehr kurz sind. Auf der anderen Seite müssen wir uns mit der Abschirmung aller Arten von Strahlung befassen, da jeder Kernreaktor eine bedeutende Quelle für alle Arten ionisierender Strahlung ist.

Berechnung der abgeschirmten Dosisleistung in Sieverts aus kontaminierten Oberflächen

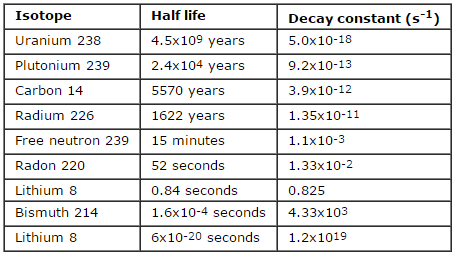
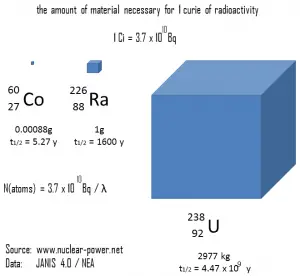
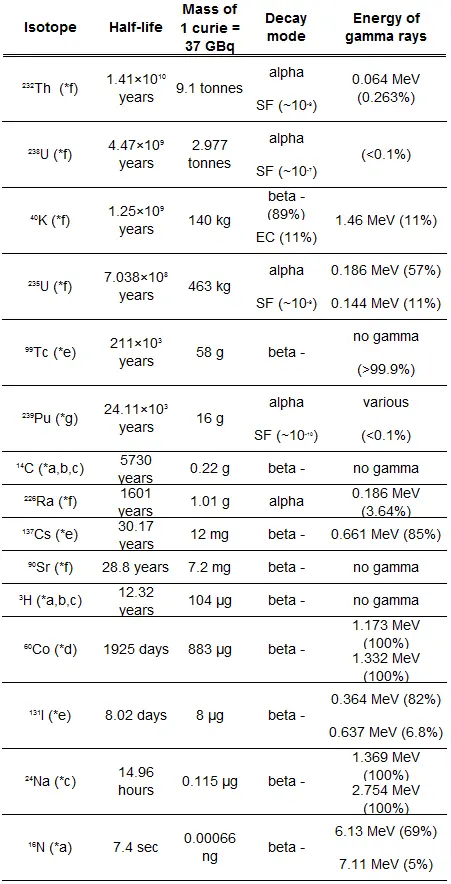
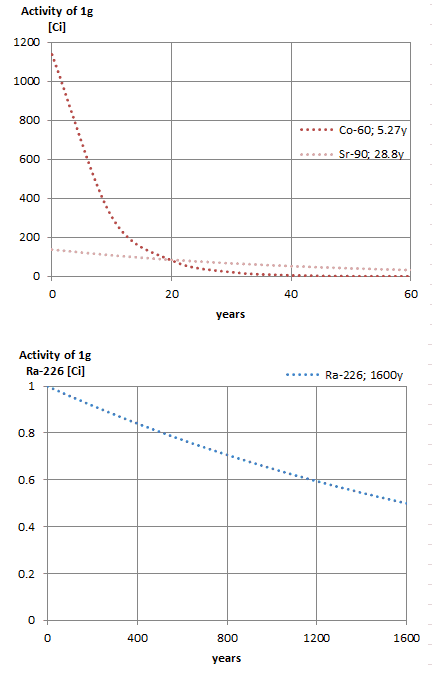
Nehmen Sie eine Oberfläche an, die durch 1,0 Ci von ¹³⁷ Cs kontaminiert ist . Angenommen, diese Verunreinigung kann durch die punktisotrope Quelle, die 1,0 Ci von ¹³⁷ Cs enthält und eine Halbwertszeit von 30,2 Jahren aufweist, geschätzt werden . Es ist zu beachten, dass die Beziehung zwischen der Halbwertszeit und der Menge eines Radionuklids, die erforderlich ist, um eine Aktivität von einem Curie zu ergeben , unten gezeigt ist. Diese Materialmenge kann mit λ berechnet werden, der Zerfallskonstante bestimmter Nuklide:

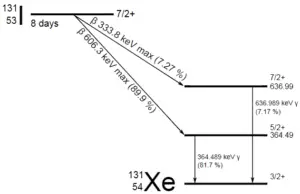
Etwa 94,6 Prozent zerfallen durch Beta-Emission zu einem metastabilen Kernisomer von Barium: Barium-137m. Der Hauptphotonenpeak von Ba-137m beträgt 662 keV . Nehmen Sie für diese Berechnung an, dass alle Zerfälle diesen Kanal durchlaufen.

Berechnen Sie die primäre Photonendosisrate in Sieverts pro Stunde (Sv.h ^-1 ) an der Außenfläche eines 5 cm dicken Bleischilds . Dann berechnet die äquivalent und wirksame Dosisraten für zwei Fälle.

Angenommen, dieses externe Strahlungsfeld durchdringt den gesamten Körper gleichmäßig . Das heißt: Berechnen Sie die effektive Ganzkörperdosis .
Angenommen, dieses externe Strahlungsfeld dringt nur in die Lunge ein und die anderen Organe sind vollständig abgeschirmt. Das heißt: Berechnen Sie die effektive Dosisleistung .

Es ist zu beachten, dass die Primärphotonendosisrate alle Sekundärteilchen vernachlässigt. Angenommen, der effektive Abstand der Quelle vom Dosispunkt beträgt 10 cm . Wir werden auch annehmen, dass der Dosispunkt Weichgewebe ist und vernünftigerweise durch Wasser simuliert werden kann, und wir verwenden den Massenenergieabsorptionskoeffizienten für Wasser.

Siehe auch: Gammastrahlendämpfung

Siehe auch: Abschirmung von Gammastrahlen

Lösung:

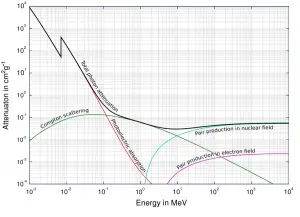
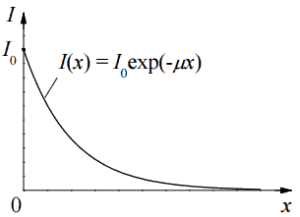
Die Primärphotonendosisrate wird exponentiell abgeschwächt , und die Dosisrate von Primärphotonen unter Berücksichtigung der Abschirmung ist gegeben durch:

Wie zu sehen ist, berücksichtigen wir den Aufbau von Sekundärstrahlung nicht. Wenn Sekundärteilchen erzeugt werden oder wenn die Primärstrahlung ihre Energie oder Richtung ändert, ist die effektive Dämpfung viel geringer. Diese Annahme unterschätzt im Allgemeinen die wahre Dosisleistung, insbesondere für dicke Schilde und wenn der Dosispunkt nahe an der Schildoberfläche liegt, aber diese Annahme vereinfacht alle Berechnungen. In diesem Fall ist die tatsächliche Dosisleistung (mit dem Aufbau von Sekundärstrahlung) mehr als doppelt so hoch.

Um die absorbierte Dosisleistung zu berechnen , müssen wir in der Formel Folgendes verwenden:

k = 5,76 · 10 & supmin; & ^sup7;
S = 3,7 × 10 ¹⁰ s ^–1
E = 0,662 MeV
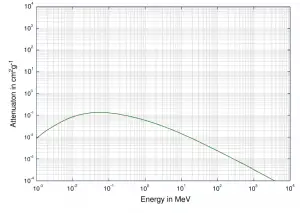
μ _t / ρ = 0,0326 cm ² / g (Werte sind bei NIST erhältlich)
μ = 1,289 cm ^-1 (Werte sind bei NIST erhältlich)
D = 5 cm
r = 10 cm

Ergebnis:

Die resultierende absorbierte Dosisrate in Grautönen pro Stunde beträgt dann:

1) Gleichmäßige Bestrahlung

Da der Strahlungsgewichtungsfaktor für Gammastrahlen gleich eins ist und wir das gleichmäßige Strahlungsfeld angenommen haben (der Gewebegewichtungsfaktor ist ebenfalls gleich eins), können wir die äquivalente Dosisrate und die effektive Dosisrate (E = H _T ) direkt berechnen ) aus der absorbierten Dosisrate als:

2) Teilbestrahlung

In diesem Fall gehen wir nur von einer teilweisen Bestrahlung der Lunge aus. Wir müssen also den Gewebegewichtungsfaktor verwenden , der gleich w _T = 0,12 ist . Der Strahlungsgewichtungsfaktor für Gammastrahlen ist gleich eins. Als Ergebnis können wir die effektive Dosisleistung wie folgt berechnen:

Beachten Sie, dass wenn ein Körperteil (z. B. die Lunge) eine Strahlendosis erhält, dies ein Risiko für eine besonders schädliche Wirkung darstellt (z. B. Lungenkrebs). Wenn die gleiche Dosis einem anderen Organ verabreicht wird, stellt dies einen anderen Risikofaktor dar.

Wenn wir den Aufbau von Sekundärstrahlung berücksichtigen wollen, müssen wir den Aufbaufaktor einbeziehen. Die erweiterte Formel für die Dosisleistung lautet dann:

Aufbaufaktoren für die Abschirmung von Gammastrahlen

Der Aufbaufaktor ist ein Korrekturfaktor, der den Einfluss der gestreuten Strahlung plus aller Sekundärteilchen im Medium bei Abschirmungsberechnungen berücksichtigt. Wenn wir den Aufbau von Sekundärstrahlung berücksichtigen wollen, müssen wir den Aufbaufaktor einbeziehen . Der Aufbaufaktor ist dann ein multiplikativer Faktor, der die Reaktion auf die nicht kollidierten Photonen berücksichtigt, um den Beitrag der gestreuten Photonen einzuschließen. Somit kann der Aufbaufaktor als Verhältnis der Gesamtdosis zur Reaktion auf die nicht kollidierte Dosis erhalten werden.

Die erweiterte Formel für die Berechnung der Dosisleistung lautet:

Der ANSI / ANS-6.4.3-1991-Gammastrahlen-Dämpfungskoeffizienten und Aufbaufaktoren für technische Materialien enthält abgeleitete Gammastrahlen-Dämpfungskoeffizienten und Aufbaufaktoren für ausgewählte technische Materialien und Elemente zur Verwendung bei Abschirmungsberechnungen (ANSI / ANS-6.1) .1, 1991).

Was ist Antineutrino – Definition

Juli 6, 2021Juli 11, 2020 von Nick Connor

Antineutrinos sind die Antiteilchen der Neutrinos. Das Antineutrino ist ein elementares subatomares Teilchen mit infinitesimaler Masse und ohne elektrische Ladung. Strahlendosimetrie

Antineutrinos sind die Antiteilchen von Neutrinos . Das Antineutrino ist ein elementares subatomares Teilchen mit infinitesimaler Masse (weniger als 0.3eV..?) und ohne elektrische Ladung. Neutrinos und Antineutrinos gehören zur Familie der Leptonen , was bedeutet, dass sie nicht über eine starke Kernkraft wechselwirken. Neutrinos sind gravitative und schwach wechselwirkende subatomare Teilchen mit einer halben Spineinheit. Auch Antineutrinos (als Neutrinos) sind sehr durchdringende subatomare Teilchen, die ohne jegliche Wechselwirkung die Erde durchdringen können. Derzeit (2015) ist nicht geklärt, ob das Neutrino und sein Antiteilchen nicht identische Teilchen sind.

Antineutrinos werden beim negativen Betazerfall produziert . In einem Kernreaktor tritt vor allem der β ⁻ -Zerfall auf, da das gemeinsame Merkmal der Spaltprodukte ein Überschuss an Neutronen ist (siehe Kernstabilität ). Ein instabiles Spaltfragment mit Neutronenüberschuss unterliegt einem β ⁻ -Zerfall, bei dem das Neutron in ein Proton, ein Elektron und ein Elektron-Antineutrino umgewandelt wird . Daher ist jeder Kernreaktor eine sehr leistungsfähige Quelle für Antineutrinos und Forscher auf der ganzen Welt untersuchen die Möglichkeiten der Verwendung von Antineutrinos für die Reaktorüberwachung.

Andererseits ist die Sonne selbst zweifellos die stärkste Quelle von Neutrinos im Sonnensystem. Milliarden solarer Neutrinos passieren pro Sekunde (meistens ohne jegliche Wechselwirkung) jeden Quadratzentimeter (~6 x 10 ¹⁰ cm ^-2 s ^-1 ) auf der Erdoberfläche. In der Sonne werden Neutrinos nach der Fusionsreaktion zweier Protonen während des positiven Beta-Zerfalls des Helium-2-Kerns erzeugt.

$_{2}^{2}textrm{He}Pfeil nach rechts _{1}^{2}textrm{H} + Beta^{+} + nu_{{e}}$

Nachweis von Antineutrinos

Da Neutrinos Materie nicht ionisieren , können sie nicht direkt nachgewiesen werden. Der Antineutrino-Nachweis (1995 Nobelpreis für Frederick Reines und Clyde Cowan) basiert auf der Reaktion:

Diese Wechselwirkung ist symmetrisch zum Beta-Zerfall von freien Neutronen , daher wird sie manchmal als inverser Beta-Zerfall bezeichnet . Alle Nachweismethoden erfordern, dass die Neutrinos eine minimale Schwellenenergie von 1,8 MeV tragen . Nur Antineutrinos mit einer Energie oberhalb der Schwelle von 1,8 MeV können Wechselwirkungen mit den Protonen im Wasser verursachen, wodurch Positronen und Neutronen entstehen .

Kernreaktor als Antineutrinoquelle

Kernreaktoren sind die Hauptquelle für vom Menschen erzeugte Antineutrinos. Dies liegt daran, dass Antineutrinos bei einem negativen Beta- Zerfall produziert werden. In einem Kernreaktor tritt vor allem der β ⁻ -Zerfall auf, denn das gemeinsame Merkmal der Spaltfragmente ist ein Überschuss an Neutronen (siehe Kernstabilität ). Ein instabiles Spaltfragment mit Neutronenüberschuss unterliegt einem β ⁻ -Zerfall, bei dem das Neutron in ein Proton, ein Elektron und ein Elektron-Antineutrino umgewandelt wird . Die Existenz der Emission von Antineutrinos und ihr sehr geringer Wirkungsquerschnitt für jede Wechselwirkung führt zu einem sehr interessanten Phänomen. Grobetwa 5% (oder etwa 12 MeV von 207 MeV) der freigesetzten Energie pro einem Spalt wird abgestrahlt aus dem Reaktor in Form von Antineutrinos. Für einen typischen Kernreaktor mit einer thermischen Leistung von 3000 MW _th (~1000 MW _e elektrischer Leistung) ist die erzeugte Gesamtleistung sogar höher, ca. 3150 MW, von denen 150 MW als Antineutrinostrahlung in den Weltraum abgestrahlt werden. Diese Energiemenge geht für immer verloren, da Antineutrinos alle Reaktormaterialien ohne Wechselwirkungen durchdringen können. Tatsächlich ist eine gängige Aussage in Physiktexten, dass die mittlere freie Weglänge eines Neutrinos ungefähr ein Lichtjahr Blei beträgt. Darüber hinaus kann ein Neutrino mittlerer Energie leicht tausend Lichtjahre Blei durchdringen (nach JB Griffiths ).

Bitte beachten Sie, dass durch jeden Quadratzentimeter (~6×10 ¹⁰ ) auf der Erdoberfläche Milliarden solarer Neutrinos pro Sekunde (meist ohne jegliche Wechselwirkung) passieren und Antineutrinostrahlung keineswegs gefährlich ist.

Beispiel – Menge an produzierten Antineutrinos:

Stabile Kerne mit der wahrscheinlichsten Massenzahl A aus der U-235- Spaltung sind $_{40}^{94}textrm{Zr}$ und $_{58}^{140}textrm{Ce}$ . Diese Kerne haben zusammen 98 Protonen und 136 Neutronen , während Spaltfragmente ( Stammkerne ) zusammen 92 Protonen und 142 Neutronen haben . Das bedeutet , dass nach jeder U-235 – Spaltung die Spaltfragmente im Durchschnitt 6 negative Beta – Zerfälle durchlaufen müssen ( 6 Neutronen müssen in 6 Protonen zerfallen ) und daher müssen pro Spaltung 6 Antineutrinos produziert werden . Der typische Kernreaktor produziert daher ca. 6 x 10 ²⁰Antineutrinos pro Sekunde (~ 200 MeV / fission; ~ 6 Antineutrinos / fission; 3000 MW _th ; 9,375 x 10 ¹⁹ fissions / sec).

Referenz: Griffiths, David, Introduction to Elementary Particles, Wiley, 1987.

Neutrino-Ereignis — Quelle: wikipedia.org

Das Innere eines zylindrischen Antineutrino-Detektors, bevor er mit einem klaren flüssigen Szintillator gefüllt wird, der Antineutrino-Wechselwirkungen durch die sehr schwachen Lichtblitze, die sie aussenden, sichtbar macht. Empfindliche Photomultiplier-Röhren säumen die Detektorwände und sind bereit, die verräterischen Blitze zu verstärken und aufzuzeichnen.
Foto: Roy Kaltschmidt, LBNL
Quelle: Daya Bay Reactor Neutrino Experiment

Antineutrino-Erkennung — Quelle: Folien – Dr. Blücher, Enrico Fermi Institut

Spaltfragmenterträge — Spaltfragmentausbeute für verschiedene Kerne. Die wahrscheinlichsten Fragmentmassen liegen um die Masse 95 (Krypton) und 137 (Barium).

Was ist Zerfallskonstante – Definition

Juli 11, 2020 von Nick Connor

Die Abklingkonstante bestimmt die Abklingrate. Die Abklingkonstante wird mit λ, „Lambda“ bezeichnet. Diese konstante Wahrscheinlichkeit kann zwischen verschiedenen Arten von Kernen stark variieren, was zu den vielen verschiedenen beobachteten Zerfallsraten führt.

Das radioaktive Zerfallsgesetz besagt, dass die Wahrscheinlichkeit pro Zeiteinheit, mit der ein Kern zerfällt, unabhängig von der Zeit konstant ist. Diese Konstante wird als Abklingkonstante bezeichnet und mit λ, „Lambda“ bezeichnet. Diese konstante Wahrscheinlichkeit kann zwischen verschiedenen Arten von Kernen stark variieren, was zu den vielen verschiedenen beobachteten Zerfallsraten führt. Der radioaktive Zerfall einer bestimmten Anzahl von Atomen (Masse) ist zeitlich exponentiell.

Gesetz des radioaktiven Zerfalls: N = Ne- ^λt

Die Rate des nuklearen Zerfalls wird auch als Halbwertszeit gemessen . Die Halbwertszeit ist die Zeit, die ein bestimmtes Isotop benötigt, um die Hälfte seiner Radioaktivität zu verlieren. Wenn ein Radioisotop eine Halbwertszeit von 14 Tagen hat, ist die Hälfte seiner Atome innerhalb von 14 Tagen zerfallen. In weiteren 14 Tagen verfällt die Hälfte der verbleibenden Hälfte und so weiter. Die Halbwertszeiten reichen von Millionstelsekunden für hochradioaktive Spaltprodukte bis zu Milliarden von Jahren für langlebige Materialien (wie natürlich vorkommendes Uran). Beachte daskurze Halbwertszeiten gehen mit großen Zerfallskonstanten einher. Radioaktives Material mit einer kurzen Halbwertszeit ist (zum Zeitpunkt der Herstellung) viel radioaktiver, verliert jedoch offensichtlich seine Radioaktivität schnell. Egal wie lang oder kurz die Halbwertszeit ist, nach Ablauf von sieben Halbwertszeiten verbleibt weniger als 1 Prozent der ursprünglichen Aktivität.

Das radioaktive Zerfallsgesetz kann auch für Aktivitätsberechnungen oder Massenberechnungen von radioaktivem Material abgeleitet werden:

(Anzahl der Kerne) N = Ne – ^λt (Aktivität) A = Ae – ^λt (Masse) m = me – ^λt

wobei N (Anzahl der Partikel) die Gesamtzahl der Partikel in der Probe ist, A (Gesamtaktivität) die Anzahl der Zerfälle pro Zeiteinheit einer radioaktiven Probe ist, m die Masse des verbleibenden radioaktiven Materials ist.

Tabelle mit Beispielen für Halbwertszeiten und Zerfallskonstanten. Beachten Sie, dass kurze Halbwertszeiten mit großen Zerfallskonstanten einhergehen. Radioaktives Material mit einer kurzen Halbwertszeit ist viel radioaktiver, verliert aber offensichtlich schnell seine Radioaktivität.

Zerfallskonstante und Halbwertszeit

Bei der Berechnung der Radioaktivität muss einer von zwei Parametern ( Zerfallskonstante oder Halbwertszeit ) bekannt sein, die die Zerfallsrate charakterisieren. Es gibt eine Beziehung zwischen der Halbwertszeit (t _1/2 ) und der Abklingkonstante λ. Die Beziehung kann durch Einstellung N = ½ N von Zerfallsgesetz ableiten _o . Das gibt:

wobei ln 2 (das natürliche log von 2) 0,693 beträgt. Wenn die Abklingkonstante (λ) angegeben ist, ist es einfach, die Halbwertszeit zu berechnen und umgekehrt.

Zerfallskonstante und Radioaktivität

Die Beziehung zwischen der Halbwertszeit und der Menge eines Radionuklids, die erforderlich ist, um eine Aktivität von einem Curie zu ergeben, ist in der Figur gezeigt. Diese Materialmenge kann mit λ berechnet werden , der Zerfallskonstante bestimmter Nuklide:

Die folgende Abbildung zeigt die Materialmenge, die für 1 Curie Radioaktivität erforderlich ist . Es ist offensichtlich, dass je länger die Halbwertszeit ist, desto mehr Radionuklid wird benötigt, um die gleiche Aktivität zu erzeugen. Natürlich bleibt die länger lebende Substanz viel länger radioaktiv. Wie zu sehen ist, kann die Menge an Material, die für 1 Curie Radioaktivität erforderlich ist, von einer zu geringen Menge (0,00088 g Cobalt-60) über 1 g Radium-226 bis zu fast drei Tonnen Uran-238 variieren .

Beispiel – Berechnung der Radioaktivität

Eine Materialprobe enthält 1 Mikrogramm Jod-131. Beachten Sie, dass Jod-131 eine wichtige Rolle als radioaktives Isotop in Kernspaltungsprodukten spielt und einen wichtigen Beitrag zu den Gesundheitsgefahren leistet, wenn es während eines Unfalls in die Atmosphäre freigesetzt wird. Jod-131 hat eine Halbwertszeit von 8,02 Tagen.

Berechnung:

Die Anzahl der anfänglich vorhandenen Iod-131-Atome.
Die Aktivität des Iod-131 in Curies.
Die Anzahl der Iod-131-Atome, die in 50 Tagen verbleiben.
Die Zeit, die die Aktivität benötigt, um 0,1 mCi zu erreichen.

Lösung:

Die Anzahl der Atome von Iod-131 kann unter Verwendung der Isotopenmasse wie folgt bestimmt werden.

N _I-131 = m _I-131 . N _A / M _I-131

N _I-131 = (1 & mgr; g ) x (6,02 × 10 ²³ Kerne / mol) / (130,91 g / mol)

N _I-131 = 4,6 × 10 ¹⁵ Kerne

Die Aktivität des Iod-131 in Curies kann anhand seiner Zerfallskonstante bestimmt werden :

Das Jod-131 hat eine Halbwertszeit von 8,02 Tagen (692928 Sekunden) und daher ist seine Zerfallskonstante:

Mit diesem Wert für die Abklingkonstante können wir die Aktivität der Probe bestimmen:

3) und 4) Die Anzahl der Iod-131-Atome, die in 50 Tagen verbleiben (N _50d ), und die Zeit, die die Aktivität benötigt, um 0,1 mCi zu erreichen, können unter Verwendung des Zerfallsgesetzes berechnet werden:

Wie zu sehen ist, wird nach 50 Tagen die Anzahl der Iod-131-Atome und damit die Aktivität etwa 75-mal geringer sein. Nach 82 Tagen ist die Aktivität ungefähr 1200-mal geringer. Daher wird die Zeit von zehn Halbwertszeiten (Faktor 2 ¹⁰ = 1024) häufig verwendet, um die Restaktivität zu definieren.

……………………………………………………………………………………………………………………………….

Dieser Artikel basiert auf der maschinellen Übersetzung des englischen Originalartikels. Weitere Informationen finden Sie im Artikel auf Englisch. Sie können uns helfen. Wenn Sie die Übersetzung korrigieren möchten, senden Sie diese bitte an: [email protected] oder füllen Sie das Online-Übersetzungsformular aus. Wir bedanken uns für Ihre Hilfe und werden die Übersetzung so schnell wie möglich aktualisieren. Danke.

Abschirmung gegen Gammastrahlung

Juli 10, 2021Juli 10, 2020 von Nick Connor

Eine wirksame Abschirmung gegen Gammastrahlung basiert auf der Verwendung von Materialien mit hoher Dichte und hohem Z-Wert. Auch Wasser und abgereichertes Uran können als Gammastrahlenschutz verwendet werden.

3-A-Regel – Abstand – Aufenthalt – Abschirmung

Im praktischen Strahlenschutz gibt es eine einfache Regel, um die Personendosis beruflich strahlenexponierter Personen möglichst niedrig zu halten. Die 3-A-Regel ist die Grundregel des Strahlenschutzes. Es besteht aus Abstand – Aufenthalt – Abschirmung.

Aufenthalt. Die Höhe der Strahlenexposition hängt direkt (linear) von der Zeit ab, die Menschen in der Nähe der Strahlungsquelle verbringen. Die Dosis kann durch Begrenzung der Expositionszeit reduziert werden .
Abstand. Die Höhe der Strahlenexposition hängt von dem Abstand von der Strahlung ab. Ähnlich wie bei einer Hitze von einem Feuer ist die Intensität der Wärmestrahlung hoch, wenn Sie zu nahe sind, und Sie können sich verbrennen. Wenn Sie in der richtigen Entfernung sind, können Sie dort problemlos standhalten und es ist außerdem bequem. Wenn Sie zu weit von der Wärmequelle entfernt sind, kann Sie auch die Unzulänglichkeit der Wärme verletzen. Diese Analogie kann in gewissem Sinne auch auf Strahlung von Strahlungsquellen angewendet werden.
Abschirmung. Wenn die Quelle zu intensiv ist und Zeit oder Entfernung keinen ausreichenden Strahlenschutz bieten, muss die Abschirmung verwendet werden. Strahlenschutz besteht normalerweise aus Barrieren aus Blei, Beton oder Wasser. Es gibt viele verschiedene Materialien, die zur Strahlenabschirmung verwendet werden können, aber es gibt viele verschiedene Situationen beim Strahlenschutz. Dies hängt stark von der Art der abzuschirmenden Strahlung, ihrer Energie und vielen anderen Parametern ab. Zum Beispiel kann sogar abgereichertes Uran als guter Schutz vor Gammastrahlung verwendet werden, andererseits ist Uran eine absolut ungeeignete Abschirmung von Neutronenstrahlung.

Eigenschaften von Gammastrahlen / Strahlung

Die Hauptmerkmale von Gammastrahlen sind in folgenden Punkten zusammengefasst:

Gammastrahlen sind hochenergetische Photonen (etwa 10 000-mal so viel Energie wie die sichtbaren Photonen), die gleichen Photonen wie die Photonen, die den sichtbaren Bereich des elektromagnetischen Spektrums bilden – Licht.
Photonen (Gammastrahlen und Röntgenstrahlen) können Atome durch den photoelektrischen Effekt und den Compton-Effekt direkt (obwohl sie elektrisch neutral sind) ionisieren, aber die sekundäre (indirekte) Ionisation ist viel bedeutender.
Gammastrahlen ionisieren Materie hauptsächlich durch indirekte Ionisation .
Obwohl eine große Anzahl möglicher Wechselwirkungen bekannt ist, gibt es drei wichtige Wechselwirkungsmechanismen mit Materie.
Gammastrahlen bewegen sich mit Lichtgeschwindigkeit und können Tausende von Metern in der Luft zurücklegen, bevor sie ihre Energie verbrauchen.
Da die Gammastrahlung sehr durchdringende Materie ist, muss sie durch sehr dichte Materialien wie Blei oder Uran abgeschirmt werden.
Die Unterscheidung zwischen Röntgen- und Gammastrahlen ist nicht so einfach und hat sich in den letzten Jahrzehnten geändert. Nach der derzeit gültigen Definition werden Röntgenstrahlen von Elektronen außerhalb des Kerns emittiert , während Gammastrahlen vom Kern emittiert werden .
Gammastrahlen begleiten häufig die Emission von Alpha- und Betastrahlung .

Vergleich von Partikeln in einer Wolkenkammer. Quelle: wikipedia.org

Dämpfungskoeffizienten. — Gesamtphotonenquerschnitte.
Quelle: Wikimedia Commons

Abschirmung gegen Gammastrahlung

Kurz gesagt basiert eine wirksame Abschirmung der Gammastrahlung in den meisten Fällen auf der Verwendung von Materialien mit zwei folgenden Materialeigenschaften:

hohe Materialdichte.
hohe Ordnungszahl des Materials (Materialien mit hohem Z)

Materialien mit niedriger Dichte und Materialien mit niedrigem Z können jedoch mit einer erhöhten Dicke kompensiert werden, die bei Abschirmanwendungen ebenso wichtig ist wie Dichte und Ordnungszahl.

Ein Blei wird häufig als Gammaschild verwendet. Der Hauptvorteil des Bleischildes liegt in seiner Kompaktheit aufgrund seiner höheren Dichte. Auf der anderen Seite ist abgereichertes Uran aufgrund seines höheren Z viel effektiver. Abgereichertes Uran wird zur Abschirmung in tragbaren Gammastrahlenquellen verwendet.

In Kernkraftwerken kann die Abschirmung eines Reaktorkerns durch Materialien des Reaktordruckbehälters, Reaktoreinbauten ( Neutronenreflektor ) erfolgen. Auch schwerer Beton wird normalerweise verwendet, um sowohl Neutronen als auch Gammastrahlung abzuschirmen .

Obwohl Wasser weder ein Material mit hoher Dichte noch mit hohem Z-Gehalt ist, wird es üblicherweise als Gammaschutz verwendet. Wasser bietet eine Strahlenabschirmung von Brennelementen in einem Pool abgebrannter Brennelemente während der Lagerung oder während des Transports vom und in den Reaktorkern .

Im Allgemeinen ist die Abschirmung der Gammastrahlung komplexer und schwieriger als die Abschirmung der Alpha- oder Betastrahlung . Um umfassend zu verstehen, wie ein Gammastrahl seine Anfangsenergie verliert, wie er abgeschwächt und abgeschirmt werden kann, müssen wir seine Interaktionsmechanismen genau kennen.

Siehe auch mehr Theorie: Wechselwirkung von Gammastrahlung mit Materie

Siehe auch Rechner: Gamma-Aktivität zur Dosisleistung (mit / ohne Schild)

Siehe auch XCOM – Photonenquerschnittsdatenbank: XCOM: Photonenquerschnittsdatenbank

Gammastrahlenabschwächung

Der Gesamtquerschnitt der Wechselwirkung von Gammastrahlen mit einem Atom ist gleich der Summe aller drei genannten Teilquerschnitte: σ = σ _f + σ _C + σ _p

σ _f – Photoelektrischer Effekt

σ _C – Compton-Effekt

σ _p – Paarbildung

Abhängig von der Gammastrahlenenergie und dem Absorbermaterial kann einer der drei Teilquerschnitte viel größer werden als die beiden anderen. Bei kleinen Werten der Gammastrahlenenergie dominiert der photoelektrische Effekt . Bei Zwischenenergien dominiert die Compton-Streuung . Die Compton-Streuung nimmt auch mit abnehmender Ordnungszahl der Materie zu, daher ist das Dominanzintervall für Lichtkerne breiter. Schließlich dominiert die Produktion von Elektronen-Positronen-Paaren bei hohen Energien.

Basierend auf der Definition des Wechselwirkungsquerschnitts kann die Abhängigkeit der Intensität der Gammastrahlen von der Dicke des Absorbermaterials abgeleitet werden. Wenn monoenergetische Gammastrahlen zu einem schmalen Strahl kollimiert werden und der Detektor hinter dem Material nur die Gammastrahlen erfasst, die durch dieses Material hindurchgegangen sind, ohne dass eine Wechselwirkung mit diesem Material besteht, sollte die Abhängigkeit eine einfache exponentielle Abschwächung der Gammastrahlen sein . Jede dieser Wechselwirkungen entfernt das Photon entweder durch Absorption oder durch Streuung von der Detektorrichtung weg vom Strahl. Daher können die Wechselwirkungen durch eine feste Eintrittswahrscheinlichkeit pro Einheit Pfadlänge im Absorber charakterisiert werden. Die Summe dieser Wahrscheinlichkeiten heißt Absorptionskoeffizient:

μ = τ _{(photoelektrisch)} + σ _(Compton) + κ _(Paar)

Gammastrahleneinstellung — Die relative Bedeutung verschiedener Prozesse der Wechselwirkung von Gammastrahlung mit Materie.

Absorptionskoeffizient

Die Dämpfung der Gammastrahlung kann dann durch die folgende Gleichung beschrieben werden.

I = I ₀ .e ^-μx

wobei I die Intensität nach der Dämpfung ist, I _o die Einfallsintensität ist, μ der Absorptionskoeffizient (cm ^–1 ) und die physikalische Dicke des Absorbers (cm) ist.

Die in der nebenstehenden Tabelle aufgeführten Materialien sind Luft, Wasser und verschiedene Elemente von Kohlenstoff ( Z = 6) bis Blei ( Z = 82). Ihre linearen Dämpfungskoeffizienten sind für drei Gammastrahlenenergien angegeben. Es gibt zwei Hauptmerkmale des Absorptionskoeffizienten:

Der lineare Dämpfungskoeffizient nimmt mit zunehmender Ordnungszahl des Absorbers zu.
Der lineare Dämpfungskoeffizient für alle Materialien nimmt mit der Energie der Gammastrahlen ab.

Halbwertsschicht

Die Halbwertsschicht drückt die Dicke des absorbierenden Materials aus, die zur Verringerung der Intensität der einfallenden Strahlung um den Faktor zwei benötigt wird . Es gibt zwei Hauptmerkmale der Halbwertsschicht:

Die Halbwertsschicht nimmt mit zunehmender Ordnungszahl des Absorbers ab. Zum Beispiel werden 35 m Luft benötigt, um die Intensität eines 100-keV-Gammastrahls um den Faktor zwei zu verringern, während nur 0,12 mm Blei dasselbe bewirken können.
Die Halbwertsschicht für alle Materialien nimmt mit der Energie der Gammastrahlen zu. Zum Beispiel von 0,26 cm für Eisen bei 100 keV bis etwa 1,06 cm bei 500 keV.

Beispiel:

Wie viel Wasserschutz benötigen Sie, wenn Sie die Intensität eines monoenergetischen 500-keV- Gammastrahls ( schmaler Strahl ) auf 1% seiner Einfallsintensität reduzieren möchten ? Die Halbwertsschicht für 500 keV Gammastrahlen in Wasser beträgt 7,15 cm und der lineare Dämpfungskoeffizient für 500 keV Gammastrahlen in Wasser beträgt 0,097 cm ^-1 . Die Frage ist recht einfach und kann durch folgende Gleichung beschrieben werden: $I (x) = frac {I_ {0}} {100} ;; wann; x =?$ Wenn die Halbwertsschicht für Wasser 7,15 cm beträgt, beträgt der lineare Dämpfungskoeffizient: $mu = frac {ln2} {7,15} = 0,097 cm ^ {- 1}$ Jetzt können wir die exponentielle Dämpfungsgleichung verwenden: $I (x) = I_0; exp; (- mu x)$ $frac {I_0} {100} = I_0; exp; (- 0,097 x)$ deshalb $frac {1} {100} =; exp; (- 0,097 x)$ $lnfrac {1} {100} = - ln; 100 = -0,097 x$ $x = frac {ln100} {{0.097}} = 47.47; cm$ Die erforderliche Wasserdicke beträgt also ca. 47,5 cm . Dies ist eine relativ große Dicke und wird durch kleine Atomzahlen von Wasserstoff und Sauerstoff verursacht. Wenn wir das gleiche Problem für Blei (Pb) berechnen , erhalten wir die Dicke x = 2,8 cm .

Lineare Dämpfungskoeffizienten

Tabelle der Absorptionskoeffizienten (in cm & supmin ; ¹ ) für verschiedene Materialien bei Gammastrahlenenergien von 100, 200 und 500 keV.

Absorber	100 keV	200 keV	500 keV
Luft	0,000195 / cm	0,000159 / cm	0,000112 / cm
Wasser	0,167 / cm	0,136 / cm	0,097 / cm
Kohlenstoff	0,335 / cm	0,274 / cm	0,196 / cm
Aluminium	0,435 / cm	0,324 / cm	0,227 / cm
Eisen	2,72 / cm	1,09 / cm	0,655 / cm
Kupfer	3,8 / cm	1,309 / cm	0,73 / cm
Führen	59,7 / cm	10,15 / cm	1,64 / cm

Halbe Wertebenen

Die Halbwertsschicht drückt die Dicke des absorbierenden Materials aus, die zur Verringerung der Intensität der einfallenden Strahlung um den Faktor zwei benötigt wird. Mit der Halbwertsschicht ist es einfach, einfache Berechnungen durchzuführen.
Quelle: www.nde-ed.org

Tabelle der Halbwertsschichten (in cm) für verschiedene Materialien bei Gammastrahlenenergien von 100, 200 und 500 keV.

Absorber	100 keV	200 keV	500 keV
Luft	3555 cm	4359 cm	6189 cm
Wasser	4,15 cm	5,1 cm	7,15 cm
Kohlenstoff	2,07 cm	2,53 cm	3,54 cm
Aluminium	1,59 cm	2,14 cm	3,05 cm
Eisen	0,26 cm	0,64 cm	1,06 cm
Kupfer	0,18 cm	0,53 cm	0,95 cm
Führen	0,012 cm	0,068 cm	0,42 cm

Massendämpfungskoeffizient

Bei der Charakterisierung eines absorbierenden Materials können wir manchmal den Massendämpfungskoeffizienten verwenden. Der Massendämpfungskoeffizient ist definiert als das Verhältnis des linearen Dämpfungskoeffizienten und der Absorberdichte (μ / ρ) . Die Dämpfung der Gammastrahlung kann dann durch die folgende Gleichung beschrieben werden:

I = I ₀ .e ^{– (μ / ρ) .ρl}

wobei ρ die Materialdichte ist, (μ / ρ) der Massendämpfungskoeffizient ist und ρ.l die Massendicke ist. Die Maßeinheit für den Massendämpfungskoeffizienten cm ² g ^-1 .

Für Zwischenenergien dominiert die Compton-Streuung und verschiedene Absorber haben ungefähr gleiche Massendämpfungskoeffizienten. Dies liegt an der Tatsache, dass der Querschnitt der Compton-Streuung proportional zum Z (Ordnungszahl) ist und daher der Koeffizient proportional zur Materialdichte ρ ist. Bei kleinen Werten der Gammastrahlenenergie oder bei hohen Werten der Gammastrahlenenergie, bei denen der Koeffizient proportional zu höheren Potenzen der Ordnungszahl Z ist (für den photoelektrischen Effekt σ _f ~ Z ⁵ ; für die Paarproduktion σ _p ~ Z ² ), wird die Der Dämpfungskoeffizient μ ist keine Konstante.

Gültigkeit des Exponentialgesetzes

Das Exponentialgesetz beschreibt immer die Dämpfung der Primärstrahlung durch Materie. Wenn Sekundärteilchen erzeugt werden oder wenn die Primärstrahlung ihre Energie oder Richtung ändert, ist die effektive Dämpfung viel geringer. Die Strahlung dringt tiefer in die Materie ein, als es das Exponentialgesetz allein vorschreibt. Der Prozess muss bei der Bewertung der Wirkung der Strahlenabschirmung berücksichtigt werden.

Beispiel für den Aufbau von Sekundärpartikeln. Hängt stark vom Charakter und den Parametern der Primärpartikel ab.

Aufbaufaktoren für die Abschirmung von Gammastrahlen

Die erweiterte Formel für die Berechnung der Dosisleistung lautet:

Was ist Beta-Zerfall – Beta-Radioaktivität – Definition

Juli 10, 2020 von Nick Connor

Der Betazerfall oder der Betazerfall repräsentiert den Zerfall eines Elternkerns zu einer Tochter durch die Emission des Betateilchens. Der Beta-Zerfall wird durch die schwache Wechselwirkung bestimmt. Strahlendosimetrie

Beta – Zerfall oder β Zerfall stellt die Desintegration eines Mutterkerns mit einer Tochter durch die Emission des Betateilchen. Dieser Übergang ( β ^– Zerfall ) kann charakterisiert werden als:

Wenn ein Kern ein Beta-Teilchen emittiert, verliert er ein Elektron (oder Positron). In diesem Fall bleibt die Massenzahl des Tochterkerns gleich, der Tochterkern bildet jedoch ein anderes Element.

Beta-Teilchen sind energiereiche, schnelle Elektronen oder Positronen, die von bestimmten Arten radioaktiver Kerne wie Kalium-40 emittiert werden. Die Beta-Partikel haben einen größeren Penetrationsbereich als Alpha-Partikel, sind aber immer noch viel kleiner als Gammastrahlen . Die emittierten Betateilchen sind eine Form ionisierender Strahlung, die auch als Betastrahlen bezeichnet wird. Es gibt folgende Formen des Beta-Zerfalls:

Negativer Beta-Zerfall – Elektronenzerfall. In Elektronen Zerfalls emittiert eine neutronenreichen Kern ein hochenergetischer Elektronen (β ^– Teilchen). Die Elektronen sind negativ geladene, fast masselose Teilchen. Aufgrund des Gesetzes zur Erhaltung der elektrischen Ladung muss sich die Kernladung um eine Einheit erhöhen. In diesem Fall kann der Prozess dargestellt werden durch:
Positiver Beta-Zerfall – Positronenzerfall. Beim Zerfall von Positronen emittiert ein protonenreicher Kern ein Positron (Positronen sind Antiteilchen von Elektronen und haben die gleiche Masse wie Elektronen, jedoch eine positive elektrische Ladung) und reduziert dadurch die Kernladung um eine Einheit. In diesem Fall kann der Prozess folgendermaßen dargestellt werden: Eine Vernichtung tritt auf, wenn ein Positron mit niedriger Energie mit einem Elektron mit niedriger Energie kollidiert.
Inverser Beta-Zerfall – Elektroneneinfang . Das Einfangen von Elektronen , auch als inverser Beta-Zerfall bekannt, wird manchmal als eine Art Beta-Zerfall bezeichnet, da der grundlegende nukleare Prozess, der durch die schwache Wechselwirkung vermittelt wird, der gleiche ist. Dabei kann ein protonenreicher Kern auch seine Kernladung um eine Einheit reduzieren, indem er ein Atomelektronen absorbiert.

Die Emission von Elektronen war eines der frühesten beobachteten Zerfallsphänomene. Der inverse Prozess, das Einfangen von Elektronen , wurde zum ersten Mal von Luis Alvarez in Vanadium 48 beobachtet. Er berichtete dies in einer Veröffentlichung von 1937 in Physical Review.

Zerfall von Uran 238. — Die Zerfallskette von Uran 238 umfasst Alpha- und Betazerfälle.

In einem Kernreaktor tritt insbesondere der β− -Zerfall auf, weil die Spaltungsprodukte einen Überschuss an Neutronen aufweisen (siehe Kernstabilität ). Ein instabiles Spaltfragment mit einem Überschuss an Neutronen unterliegt einem β− -Zerfall, bei dem das Neutron in ein Proton, ein Elektron und ein Elektron-Antineutrino umgewandelt wird . Ein freies Neutron unterliegt ebenfalls dieser Art von Zerfall. Ein freies Neutron zerfällt mit einer Halbwertszeit von etwa 611 Sekunden (10,3 Minuten) in ein Proton, ein Elektron und ein Antineutrino (das Antimaterie- Gegenstück des Neutrinos , ein Teilchen ohne Ladung und ohne oder mit geringer Masse).

Theorie des Beta-Zerfalls – Schwache Interaktion

Der Beta-Zerfall wird durch die schwache Wechselwirkung bestimmt . Während der Beta – Zerfall eines von zwei nach unten Quark Veränderungen in einen up Quark durch einen W Emittieren ^– Bosonen (wegträgt , eine negative Ladung). Das W ^– Boson zerfällt dann in ein Beta – Teilchen und ein Antineutrino . Dieser Prozess entspricht dem Prozess, bei dem ein Neutrino mit einem Neutron interagiert.

Wie aus der Abbildung ersichtlich ist, ändert die schwache Wechselwirkung einen Quarkgeschmack in einen anderen. Beachten Sie, dass das Standardmodell sechs Geschmacksrichtungen von Quarks und sechs Geschmacksrichtungen von Leptonen zählt. Die schwache Wechselwirkung ist der einzige Prozess, bei dem ein Quark zu einem anderen Quark oder ein Lepton zu einem anderen Lepton wechseln kann (Geschmacksänderung). Weder die starke Wechselwirkung noch elektromagnetischGeschmacksänderung zulassen. Diese Tatsache ist bei vielen Zerfällen von Kernteilchen von entscheidender Bedeutung. Bei dem Fusionsprozess, der beispielsweise die Sonne antreibt, interagieren zwei Protonen über die schwache Kraft zu einem Deuteriumkern, der weiter reagiert und Helium erzeugt. Ohne die schwache Wechselwirkung würde das Diproton durch Protonenemission in zwei ungebundene Wasserstoff-1-Protonen zurückfallen. Infolgedessen würde die Sonne ohne sie nicht brennen, da die schwache Wechselwirkung die Transmutation p -> n verursacht.

Im Gegensatz zum Alpha-Zerfall existieren weder das Beta-Teilchen noch das zugehörige Neutrino vor dem Beta-Zerfall im Kern, sondern entstehen beim Zerfall. Durch diesen Prozess erhalten instabile Atome ein stabileres Verhältnis von Protonen zu Neutronen. Die Wahrscheinlichkeit, dass ein Nuklid aufgrund von Beta und anderen Formen des Zerfalls zerfällt, wird durch seine Kernbindungsenergie bestimmt. Damit eine Elektronen- oder Positronenemission energetisch möglich ist, muss die Energiefreisetzung (siehe unten) oder der Q-Wert positiv sein.

Beispiel für Beta-Zerfall

Freies Neutron
Entdeckung von Neutrino
Beta-Zerfall von Tritium

Energiespektrum des Beta-Zerfalls

Sowohl beim Alpha- als auch beim Gamma-Zerfall weist das resultierende Teilchen ( Alpha-Teilchen oder Photon ) eine enge Energieverteilung auf , da das Teilchen die Energie aus der Differenz zwischen dem Anfangs- und dem Endkernzustand trägt. Wenn beispielsweise im Fall eines Alpha-Zerfalls ein Elternkern spontan zerfällt und einen Tochterkern und ein Alpha-Teilchen ergibt, entspricht die Summe der Masse der beiden Produkte nicht ganz der Masse des ursprünglichen Kerns (siehe Massendefekt ). . Aufgrund des Energieerhaltungsgesetzes tritt dieser Unterschied in Form der kinetischen Energie des Alpha-Teilchens auf. Da bei jedem Abbau eines bestimmten Elternkerns dieselben Partikel als Produkte auftreten, sollte die Massendifferenz immer gleich sein , und die kinetische Energie der Alpha-Partikel sollte auch immer gleich sein. Mit anderen Worten, der Strahl von Alpha-Partikeln sollte monoenergetisch sein .

Es wurde erwartet, dass die gleichen Überlegungen für einen Elternkern gelten würden, der in einen Tochterkern und ein Beta-Teilchen zerfällt . Da nur das Elektron und der rückprallende Tochterkern Beta-Zerfall beobachtet wurden, wurde zunächst angenommen, dass der Prozess ein Zweikörperprozess ist , der dem Alpha-Zerfall sehr ähnlich ist. Es erscheint vernünftig anzunehmen, dass die Beta-Partikel auch einen monoenergetischen Strahl bilden würden .

Um zu demonstrieren , Energetik von Zwei-Körper – Beta – Zerfall, betrachten den Beta – Zerfall , in der ein Elektron emittiert wird , und der Mutterkern im Ruhezustand ist , c onservation Energie erfordert:

Da das Elektron ein viel leichteres Teilchen ist, wurde erwartet, dass es den größten Teil der freigesetzten Energie _abführt , die einen einzigartigen Wert T _{e- haben würde} .

Energiespektrum des Beta-Zerfalls — Die Form dieser Energiekurve hängt davon ab, welcher Anteil der Reaktionsenergie (Q-Wert – die durch die Reaktion freigesetzte Energiemenge) vom Elektron oder Neutrino getragen wird.

Aber die Realität sah anders aus . Das von Lise Meitner und Otto Hahn 1911 und von Jean Danysz 1913 gemessene Spektrum von Beta-Partikeln zeigte jedoch mehrere Linien auf einem diffusen Hintergrund. Darüber hinaus haben praktisch alle emittierten Beta-Partikel Energien, die unter denen liegen, die durch Energieeinsparung bei Zweikörperzerfällen vorhergesagt werden. Die beim Beta-Zerfall emittierten Elektronen haben eher ein kontinuierliches als ein diskretes Spektrum , was der Energieerhaltung zu widersprechen scheint, unter der damals aktuellen Annahme, dass der Beta-Zerfall die einfache Emission eines Elektrons aus einem Kern ist. Als dies zum ersten Mal beobachtet wurde, schien es das Überleben eines der wichtigsten Naturschutzgesetze in der Physik zu gefährden !

Um diese Energiefreisetzung zu erklären, schlug Pauli (1931) vor, dass beim Zerfall ein weiteres Teilchen emittiert wurde , das später von Fermi als Neutrino bezeichnet wurde . Es war klar, dass dieses Teilchen stark durchdringen muss und dass die Erhaltung der elektrischen Ladung erfordert, dass das Neutrino elektrisch neutral ist. Dies würde erklären, warum es so schwierig war, dieses Teilchen zu erkennen. Der Begriff Neutrino kommt aus dem Italienischen und bedeutet „kleines neutrales“. Neutrinos werden mit dem griechischen Buchstaben ν (nu) bezeichnet . Während des Beta-Zerfalls trägt das Neutrino die fehlende Energie und auch in diesem Prozess bleibt das Gesetz der Energieerhaltung gültig .

Naturschutzgesetze im Beta-Zerfall

Bei der Analyse von Kernreaktionen wenden wir die vielen Erhaltungsgesetze an . Kernreaktionen unterliegen den klassischen Erhaltungsgesetzen für Ladung, Impuls, Drehimpuls und Energie (einschließlich Ruheenergien). Zusätzliche Erhaltungsgesetze, die von der klassischen Physik nicht erwartet werden, sind:

Bestimmte dieser Gesetze werden unter allen Umständen eingehalten, andere nicht. Wir haben die Erhaltung von Energie und Dynamik akzeptiert. In allen Beispielen nehmen wir an, dass die Anzahl der Protonen und die Anzahl der Neutronen getrennt erhalten bleiben. Wir werden Umstände und Bedingungen finden, unter denen diese Regel nicht wahr ist. Wenn wir nicht-relativistische Kernreaktionen betrachten, ist dies im Wesentlichen wahr. Wenn wir jedoch relativistische Kernenergien oder solche mit schwachen Wechselwirkungen betrachten, werden wir feststellen, dass diese Prinzipien erweitert werden müssen.

Einige Erhaltungsprinzipien sind aus theoretischen Überlegungen hervorgegangen, andere sind nur empirische Beziehungen. Ungeachtet dessen wird jede Reaktion, die nicht ausdrücklich durch die Erhaltungsgesetze verboten ist, im Allgemeinen auftreten, wenn auch nur langsam. Diese Erwartung basiert auf der Quantenmechanik. Sofern die Barriere zwischen dem Anfangs- und dem Endzustand nicht unendlich hoch ist, besteht immer eine Wahrscheinlichkeit ungleich Null, dass ein System den Übergang zwischen ihnen vollzieht.

Zur Analyse nicht-relativistischer Reaktionen genügt es, vier der Grundgesetze zu beachten, die diese Reaktionen regeln.

Erhaltung der Nukleonen . Die Gesamtzahl der Nukleonen vor und nach einer Reaktion ist gleich.
Ladungserhaltung . Die Summe der Ladungen aller Partikel vor und nach einer Reaktion ist gleich
Impulserhaltung . Der Gesamtimpuls der wechselwirkenden Teilchen vor und nach einer Reaktion ist der gleiche.
Energieeinsparung . Energie, einschließlich Ruhemassenenergie, bleibt bei Kernreaktionen erhalten.

Referenz: Lamarsh, John R. Einführung in die Nukleartechnik 2. Auflage

Beta-Zerfall – Q-Wert

In der Kern- und Teilchenphysik wird die Energetik von Kernreaktionen durch den Q-Wert dieser Reaktion bestimmt. Der Q-Wert der Reaktion wird als die definierte Differenz zwischen der Summe der übrigen Masse der anfänglichen Reaktanten und der Summe der Massen der Endprodukte , in Energieeinheiten ( in der Regel in MeV).

Stellen Sie sich eine typische Reaktion vor, bei der das Projektil a und das Ziel A zwei Produkten Platz machen, B und b. Dies kann auch in der bisher verwendeten Notation a + A → B + b oder sogar in einer kompakteren Notation A (a, b) B ausgedrückt werden .

Siehe auch: E = mc2

Der Q-Wert dieser Reaktion ist gegeben durch:

Q = [ma + mA – (mb + mB)] c ²

Bei der Beschreibung des Beta-Zerfalls (Reaktion ohne Projektil) wird der zerfallende Kern üblicherweise als Elternkern und der nach dem Ereignis verbleibende Kern als Tochterkern bezeichnet. Die Emission eines Beta-Teilchens, entweder eines Elektrons β ^– oder eines Positrons β ⁺ , ändert die Ordnungszahl des Kerns, ohne dessen Massenzahl zu beeinflussen. Die gesamte Ruhemasse des Tochterkerns und der bei einem Beta-Zerfall freigesetzten Kernstrahlung, m _Tochter + m _Strahlung , ist immer geringer als die des Elternkerns, m _Eltern .

Der Masse-Energie-Unterschied,

Q = [m _Elternteil – (m _Tochter + m _Strahlung )] c ²

erscheint als die Zerfallsenergie, die dabei freigesetzt wird. Zum Beispiel ist der Q-Wert eines typischen Beta-Zerfalls:

Beim Beta-Zerfall wird entweder ein Elektron oder ein Positron emittiert. Diese Emission geht mit der Emission von Antineutrino (β-Zerfall) oder Neutrino (β + Zerfall) einher , die Energie und Impuls des Zerfalls teilen. Die Beta-Emission hat ein charakteristisches Spektrum. Dieses charakteristische Spektrum wird durch die Tatsache verursacht, dass entweder ein Neutrino oder ein Antineutrino unter Emission von Beta-Partikeln emittiert wird. Die Form dieser Energiekurve hängt davon ab, welcher Anteil der Reaktionsenergie ( Q-Wert – die durch die Reaktion freigesetzte Energiemenge) vom massiven Teilchen getragen wird. Beta-Partikel können daher mit jeder kinetischen Energie im Bereich von 0 bis Q emittiert werden. Nach einem Alpha- oder Beta-Zerfall befindet sich der Tochterkern häufig in einem angeregten Energiezustand. Um sich zu stabilisieren, emittiert es anschließend hochenergetische Photonen, γ-Strahlen.

……………………………………………………………………………………………………………………………….

Was ist Alpha-Zerfall – Alpha-Radioaktivität – Definition

Juli 10, 2020 von Nick Connor

Der Alpha-Zerfall oder der α-Zerfall repräsentiert den Zerfall eines Elternkerns zu einer Tochter durch die Emission des Kerns eines Heliumatoms. Der Alpha-Zerfall ist ein Quantentunnelungsprozess. Um emittiert zu werden, muss das Alpha-Teilchen eine Potentialbarriere durchdringen. Strahlendosimetrie

Alpha-Zerfall (oder α-Zerfall und auch Alpha-Radioaktivität ) bezeichnet den Zerfall eines Elternkerns zu einer Tochter durch die Emission des Kerns eines Heliumatoms. Dieser Übergang kann charakterisiert werden als:

Wie aus der Abbildung ersichtlich ist, werden Alphateilchen beim Alpha-Zerfall emittiert. Alpha-Teilchen sind energetische Heliumkerne . Alpha-Teilchen bestehen aus zwei Protonen und zwei Neutronen , die zu einem Teilchen verbunden sind, das mit einem Heliumkern identisch ist. Alpha-Teilchen sind relativ groß und doppelt positiv geladen. Sie sind nicht sehr durchdringend und ein Stück Papier kann sie aufhalten. Sie bewegen sich nur wenige Zentimeter, geben aber auf ihren kurzen Wegen alle Energie ab.

In der Praxis wurde dieser Zerfallsmodus nur bei Nukliden beobachtet, die erheblich schwerer als Nickel sind, wobei die leichtesten bekannten Alpha-Emitter die leichtesten Isotope (Massenzahlen 106–110) von Tellur (Element 52) sind. In Kernreaktoren kommt es beispielsweise im Brennstoff zum Alpha-Zerfall (Alpha-Zerfall schwerer Kerne). Alpha-Partikel werden üblicherweise von allen in der Natur vorkommenden schweren radioaktiven Kernen ( Uran , Thorium oder Radium) sowie den transuranischen Elementen (Neptunium, Plutonium oder Americium) emittiert .

Theorie des Alpha-Zerfalls – Quantentunneln

Unter der Vielzahl von Kanälen, in denen ein Kern zerfällt, war der Alpha-Zerfall einer der am meisten untersuchten. Der Alpha-Zerfallskanal in schweren und superschweren Kernen lieferte Informationen über die grundlegenden Eigenschaften von Kernen, die weit von der Stabilität entfernt sind, wie z. B. ihre Grundzustandsenergien und die Struktur ihres Kernniveaus.

Der Alpha-Zerfall ist ein Quantentunnelungsprozess . Um emittiert zu werden, muss das Alpha-Teilchen eine Potentialbarriere durchdringen. Dies ähnelt dem Clusterzerfall , bei dem ein Atomkern einen kleinen „Cluster“ von Neutronen und Protonen (z . B. ¹² C) emittiert .

Die Höhe der Coulomb-Barriere für Kerne von A «200 beträgt etwa 20-25 MeV . Die beim Kernzerfall emittierten Alpha-Teilchen haben typische Energien von etwa 5 MeV. Einerseits wird ein ankommendes 5-MeV-Alpha-Teilchen von einem schweren Kern gestreut, und es kann die Coulomb-Barriere nicht durchdringen und kommt dem Kern so nahe, dass es durch die starke Kraft interagieren kann. Andererseits kann ein 5-MeV-Alpha-Teilchen, das in einem Kernpotentialtopf gebunden ist, dieselbe Coulomb-Barriere tunneln.

Bis 1928 hatte George Gamow (und unabhängig von Ronald Gurney und Edward Condon ) die Theorie des Alpha-Zerfalls durch Quantentunneln gelöst. Sie nahmen an, dass das Alpha-Teilchen und der Tochterkern vor seiner Dissoziation im Elternkern existieren, nämlich beim Zerfall der quasistationären Zustände (QS). Ein quasistationärer Zustand ist definiert als ein langlebiger Zustand, der schließlich zerfällt. Anfänglich oszilliert der Alpha-Cluster im Potential des Tochterkerns, wobei das Coulomb-Potential deren Trennung verhindert. Das Alpha-Teilchen wird vom Kern in einer Potentialwanne gefangen. Klassisch ist es verboten zu entkommen, aber nach den (damals) neu entdeckten Prinzipien der Quantenmechanik besteht eine winzige (aber nicht null) Wahrscheinlichkeit, dass es durch die Barriere „tunnelt“ und auf der anderen Seite erscheint, um dem Kern zu entkommen . Gamow, Condon und Gurney berechneten unter Verwendung des Tunnelmechanismus die Penetrierbarkeit des Tunnel-α-Partikels durch die Coulomb-Barriere. Ermittlung der Lebensdauern einiger α-emittierender Kerne. Der Haupterfolg dieses Modells war die Reproduktion des semi-empirischen Geiger-Nuttall-Gesetzes, das die Lebensdauern der α-Emitter in Bezug auf die Energien der freigesetzten α-Teilchen ausdrückt. Es ist zu beachten, dass andere übliche Zerfallsformen (z. B. Beta-Zerfall) durch das Zusammenspiel von Kernkraft und elektromagnetischer Kraft bestimmt werden.

Spezielle Referenz: WSC Williams. Kern- und Teilchenphysik. Clarendon Press; 1 edition, 1991, ISBN: 978-0198520467.

Geiger-Nuttall-Gesetz

Das Geiger-Nuttall-Gesetz ist ein semi-empirisches Gesetz, das die Lebensdauer (Halbwertszeit) des Alpha-Emitters als Energie des freigesetzten Alpha-Teilchens ausdrückt. Mit anderen Worten heißt es, dass kurzlebige Isotope mehr energetische Alpha-Partikel emittieren als langlebige. Diese Regel wurde 1911 von Hans Geiger und John Mitchell Nuttall vor der Entwicklung der theoretischen Formulierung formuliert. Das Geiger-Nuttall-Gesetz kann mathematisch ausgedrückt werden als:

Dabei sind a und b empirische Konstanten, die aus logarithmischen Darstellungen experimenteller Daten ermittelt werden. R _α stellt den linearen Bereich des Alpha-Teilchens dar und ist somit ein direktes Maß für die kinetische Energie des Alpha-Teilchens. Die Breite der Resonanz (Γ) hängt im Allgemeinen mit der mittleren Lebensdauer (τ) des angeregten Kerns durch die Beziehung zusammen: Γ = ℏ / τ

Naturschutzgesetze im Alpha-Zerfall

Zur Analyse nicht-relativistischer Reaktionen genügt es, vier der Grundgesetze zu beachten, die diese Reaktionen regeln.

Erhaltung der Nukleonen . Die Gesamtzahl der Nukleonen vor und nach einer Reaktion ist gleich.
Ladungserhaltung . Die Summe der Ladungen aller Partikel vor und nach einer Reaktion ist gleich
Impulserhaltung . Der Gesamtimpuls der wechselwirkenden Teilchen vor und nach einer Reaktion ist der gleiche.
Energieeinsparung . Energie, einschließlich Ruhemassenenergie, bleibt bei Kernreaktionen erhalten.

Referenz: Lamarsh, John R. Einführung in die Nukleartechnik 2. Auflage

Alpha-Zerfall – Q-Wert

Siehe auch: E = mc2

Der Q-Wert dieser Reaktion ist gegeben durch:

Q = [ma + mA – (mb + mB)] c ²

Bei der Beschreibung des Alpha-Zerfalls (einer Reaktion ohne Projektil) wird der zerfallende Kern üblicherweise als Elternkern und der nach dem Ereignis verbleibende Kern als Tochterkern bezeichnet. Die gesamte Ruhemasse des Tochterkerns und der bei einer Alpha-Auflösung freigesetzten Kernstrahlung, m _Tochter + m _Strahlung , ist immer geringer als die des Elternkerns, m _Eltern . Der Masse-Energie-Unterschied,

Q = [m _Elternteil – (m _Tochter + m _Strahlung )] c ²

erscheint als die Zerfallsenergie, die dabei freigesetzt wird. Zum Beispiel ist der Q-Wert eines typischen Alpha-Zerfalls:

Die Zerfallsenergie von etwa 5 MeV ist eine typische kinetische Energie von Alpha-Teilchen. Um das Gesetz der Impulserhaltung zu erfüllen, muss der größte Teil der Zerfallsenergie als kinetische Energie des Alpha-Teilchens erscheinen. Nach einem Alpha- oder Beta-Zerfall befindet sich der Tochterkern häufig in einem angeregten Energiezustand. Um sich zu stabilisieren, emittiert es anschließend hochenergetische Photonen, γ-Strahlen.

……………………………………………………………………………………………………………………………….

Was ist Halbwertszeit – Berechnung – Beispiel – Definition

Juli 10, 2020 von Nick Connor

Halbwertszeit – Berechnung – Beispiel. Jod-131 hat eine Halbwertszeit von 8,02 Tagen. Berechnen Sie die Aktivität von Jod-131 in Curies. Strahlendosimetrie

Einer der nützlichsten Begriffe zur Abschätzung, wie schnell ein Nuklid zerfällt, ist die radioaktive Halbwertszeit ( t _1/2 ). Die Halbwertszeit ist definiert als die Zeit, die ein bestimmtes Isotop benötigt, um die Hälfte seiner Radioaktivität zu verlieren. Wie bereits geschrieben, ist der radioaktive Zerfall ein zufälliger Vorgang auf der Ebene einzelner Atome, da nach der Quantentheorie nicht vorhergesagt werden kann, wann ein bestimmtes Atom zerfallen wird. Mit anderen Worten, ein Kern eines Radionuklids hat kein „Gedächtnis“. Ein Kern „altert“ nicht im Laufe der Zeit. Somit steigt die Wahrscheinlichkeit seines Zerfalls nicht mit der Zeit, sondern bleibt konstant, egal wie lange der Kern existiert hat.

Daher kann die Rate des nuklearen Zerfalls auch als Halbwertszeit gemessen werden . Jedes Radionuklid hat seine eigene Halbwertszeit, die sich unabhängig von der Menge oder Form des Materials (dh Feststoff, Flüssigkeit, Gas, Element oder Verbindung) oder seiner Vorgeschichte niemals ändert. Wenn ein Radioisotop eine Halbwertszeit von 14 Tagen hat, ist die Hälfte seiner Atome innerhalb von 14 Tagen zerfallen. In weiteren 14 Tagen verfällt die Hälfte der verbleibenden Hälfte und so weiter.

Die Halbwertszeiten reichen von Millionstelsekunden für hochradioaktive Spaltprodukte bis zu Milliarden von Jahren für langlebige Materialien (wie natürlich vorkommendes Uran). Nach Ablauf von fünf Halbwertszeiten verbleiben nur noch 1/32 oder 3,1% der ursprünglichen Anzahl von Atomen. Nach sieben Halbwertszeiten sind nur noch 1/128 oder 0,78% der Atome übrig. Die Anzahl der Atome, die nach 5 bis 7 Halbwertszeiten existieren, kann normalerweise als vernachlässigbar angesehen werden.

Halbwertszeit und Radioaktivität – Beispiel

Die folgende Abbildung zeigt die Menge an Material, die für 1 Curie Radioaktivität erforderlich ist . Es ist offensichtlich, dass je länger die Halbwertszeit ist, desto mehr Radionuklid wird benötigt, um die gleiche Aktivität zu erzeugen. Natürlich bleibt die länger lebende Substanz viel länger radioaktiv. Wie zu sehen ist, kann die Menge an Material, die für 1 Curie Radioaktivität erforderlich ist, von einer zu geringen Menge (0,00088 Gramm Cobalt-60) über 1 Gramm Radium-226 bis zu fast drei Tonnen Uran-238 variieren .

Beispiel – Radioaktives Zerfallsgesetz

Eine Materialprobe enthält 1 Mikrogramm Jod-131. Es ist zu beachten, dass Iod-131 eine wichtige Rolle als radioaktives Isotop in Kernspaltungsprodukten spielt und einen wesentlichen Beitrag zu den Gesundheitsgefahren leistet, wenn es während eines Unfalls in die Atmosphäre freigesetzt wird. Jod-131 hat eine Halbwertszeit von 8,02 Tagen.

Berechnung:

Die Anzahl der anfänglich vorhandenen Iod-131-Atome.
Die Aktivität des Iod-131 in Curies.
Die Anzahl der Iod-131-Atome, die in 50 Tagen verbleiben.
Die Zeit, die die Aktivität benötigt, um 0,1 mCi zu erreichen.

Lösung:

Die Anzahl der Atome von Iod-131 kann unter Verwendung der Isotopenmasse wie folgt bestimmt werden.

N _I-131 = m _I-131 . N _A / M _I-131

N _I-131 = (1 & mgr; g ) x (6,02 × 10 ²³ Kerne / mol) / (130,91 g / mol)

N _I-131 = 4,6 × 10 ¹⁵ Kerne

Die Aktivität des Iod-131 in Curies kann anhand seiner Zerfallskonstante bestimmt werden :

Bei der Berechnung der Radioaktivität muss einer von zwei Parametern ( Zerfallskonstante oder Halbwertszeit ) bekannt sein, die die Zerfallsrate charakterisieren. Es gibt eine Beziehung zwischen der Halbwertszeit (t _1/2 ) und der Abklingkonstante λ. Die Beziehung kann aus dem Zerfallsgesetz abgeleitet werden, indem N = ½ N _{o gesetzt wird} . Das gibt:

wobei ln 2 (das natürliche log von 2) gleich 0,693 ist. Wenn die Abklingkonstante (λ) angegeben ist, ist es einfach, die Halbwertszeit zu berechnen und umgekehrt.

Das Jod-131 hat eine Halbwertszeit von 8,02 Tagen (692928 Sekunden) und daher ist seine Zerfallskonstante:

Mit diesem Wert für die Abklingkonstante können wir die Aktivität der Probe bestimmen:

……………………………………………………………………………………………………………………………….

Was ist radioaktive Halbwertszeit – physikalische Halbwertszeit – Definition

Juli 7, 2021Juli 10, 2020 von Nick Connor

Einer der nützlichsten Begriffe für die Abschätzung, wie schnell ein Nuklid zerfällt, ist die radioaktive Halbwertszeit (t1 / 2). Die Halbwertszeit ist definiert als die Zeit, die ein bestimmtes Isotop benötigt, um die Hälfte seiner Radioaktivität zu verlieren.

Der Anteil der ursprünglichen Aktivität, der nach den folgenden Halbwertszeiten verbleibt, beträgt:

Aktivität nach 1 Halbwertszeit = ½ des Originals

Aktivität nach 2 Halbwertszeiten = ½ x ½ = ¼ des Originals

Aktivität nach 3 Halbwertszeiten = ½ x ½ x ½ = (½) ³ = 1/8 des Originals

Aktivität nach 4 Halbwertszeiten = (½) ⁴ = 1/16 des Originals

Aktivität nach 5 Halbwertszeiten = (½) ⁵ = 1/32 des Originals

Aktivität nach 6 Halbwertszeiten = (½) ⁶ = 1/64 des Originals

Aktivität nach 7 Halbwertszeiten = (½) ⁷ = 1/128 des Originals

Beachten Sie, dass kurze Halbwertszeiten mit großen Zerfallskonstanten einhergehen. Radioaktives Material mit einer kurzen Halbwertszeit ist (zum Zeitpunkt der Herstellung) viel radioaktiver, verliert jedoch offensichtlich schnell seine Radioaktivität. Unabhängig davon, wie lang oder kurz die Halbwertszeit ist, bleibt nach Ablauf von sieben Halbwertszeiten weniger als 1 Prozent der ursprünglichen Aktivität übrig.

Das Gesetz über den radioaktiven Zerfall besagt, dass die Wahrscheinlichkeit pro Zeiteinheit, dass ein Kern zerfällt, unabhängig von der Zeit konstant ist. Diese Konstante wird als Abklingkonstante bezeichnet und mit λ, „Lambda“, bezeichnet. Diese konstante Wahrscheinlichkeit kann zwischen verschiedenen Arten von Kernen stark variieren, was zu den vielen verschiedenen beobachteten Zerfallsraten führt. Der radioaktive Zerfall einer bestimmten Anzahl von Atomen (Masse) ist zeitlich exponentiell.

Gesetz über den radioaktiven Zerfall: N = Ne- ^λt

Die Rate des nuklearen Zerfalls wird auch als Halbwertszeit gemessen . Die Halbwertszeit ist die Zeit, die ein bestimmtes Isotop benötigt, um die Hälfte seiner Radioaktivität zu verlieren. Wenn ein Radioisotop eine Halbwertszeit von 14 Tagen hat, ist die Hälfte seiner Atome innerhalb von 14 Tagen zerfallen. In weiteren 14 Tagen wird die Hälfte der verbleibenden Hälfte verfallen und so weiter. Die Halbwertszeiten reichen von Millionstelsekunden für hochradioaktive Spaltprodukte bis zu Milliarden von Jahren für langlebige Materialien (wie natürlich vorkommendes Uran). Beachte dasKurze Halbwertszeiten gehen mit großen Zerfallskonstanten einher. Radioaktives Material mit einer kurzen Halbwertszeit ist (zum Zeitpunkt der Herstellung) viel radioaktiver, verliert jedoch offensichtlich schnell seine Radioaktivität. Unabhängig davon, wie lang oder kurz die Halbwertszeit ist, bleibt nach Ablauf von sieben Halbwertszeiten weniger als 1 Prozent der ursprünglichen Aktivität übrig.

Das Gesetz über den radioaktiven Zerfall kann auch für Aktivitätsberechnungen oder Massenberechnungen für radioaktives Material abgeleitet werden:

(Anzahl der Kerne) N = Ne- ^λt (Aktivität) A = Ae- ^λt (Masse) m = me- ^λt

Halbwertszeit und Zerfallskonstante

Bei der Berechnung der Radioaktivität muss einer von zwei Parametern ( Zerfallskonstante oder Halbwertszeit ) bekannt sein, die die Zerfallsrate charakterisieren. Es gibt eine Beziehung zwischen der Halbwertszeit (t _1/2 ) und der Abklingkonstante λ. Die Beziehung kann aus dem Zerfallsgesetz abgeleitet werden, indem N = ½ N _{o gesetzt wird} . Das gibt:

wobei ln 2 (das natürliche log von 2) gleich 0,693 ist. Wenn die Abklingkonstante (λ) angegeben ist, ist es einfach, die Halbwertszeit zu berechnen und umgekehrt.

Halbwertszeit und Radioaktivität

Beispiel – Gesetz über radioaktiven Zerfall

Berechnung:

Die Anzahl der anfänglich vorhandenen Iod-131-Atome.
Die Aktivität des Iod-131 in Curies.
Die Anzahl der Iod-131-Atome, die in 50 Tagen verbleiben.
Die Zeit, die die Aktivität benötigt, um 0,1 mCi zu erreichen.

Lösung:

Die Anzahl der Atome von Iod-131 kann unter Verwendung der Isotopenmasse wie folgt bestimmt werden.

N _I-131 = m _I-131 . N _A / M _I-131

N _I-131 = (1 & mgr; g ) x (6,02 × 10 ²³ Kerne / mol) / (130,91 g / mol)

N _I-131 = 4,6 × 10 ¹⁵ Kerne

Die Aktivität des Iod-131 in Curies kann anhand seiner Zerfallskonstante bestimmt werden :

Das Jod-131 hat eine Halbwertszeit von 8,02 Tagen (692928 Sekunden) und daher ist seine Zerfallskonstante:

Mit diesem Wert für die Abklingkonstante können wir die Aktivität der Probe bestimmen:

Biologische Halbwertszeit

Im Allgemeinen ist die biologische Halbwertszeit die Zeit, die benötigt wird, um die Menge eines bestimmten Elements im Körper auf die Hälfte seines Anfangswertes zu verringern, allein aufgrund der Eliminierung durch biologische Prozesse, wenn die Entfernungsrate ungefähr exponentiell ist. Die biologische Halbwertszeit (t _biologisch ) kann für Metaboliten, Arzneimittel und andere Substanzen definiert werden. Dies ist auch beim Strahlenschutz sehr wichtig, wenn die interne Exposition berücksichtigt wird.

Wenn sich die Strahlungsquelle in unserem Körper befindet, sagen wir, handelt es sich um eine innere Exposition. Die Aufnahme von radioaktivem Material kann über verschiedene Wege erfolgen, z. B. durch Aufnahme radioaktiver Kontamination in Lebensmitteln oder Flüssigkeiten, Einatmen radioaktiver Gase oder durch intakte oder verletzte Haut. Die meisten Radionuklide geben Ihnen viel mehr Strahlendosis, wenn sie irgendwie in Ihren Körper gelangen können, als wenn sie draußen bleiben würden. Die biologische Halbwertszeit hängt von der Geschwindigkeit ab, mit der der Körper normalerweise eine bestimmte Verbindung eines Elements verwendet. Radioaktive Isotope, die über andere Wege aufgenommen oder aufgenommen wurden, werden nach und nach über Darm, Nieren, Atmung und Schweiß aus dem Körper entfernt. Dies bedeutet, dass eine radioaktive Substanz ausgestoßen werden kann, bevor sie zerfallen kann.

Infolgedessen beeinflusst die biologische Halbwertszeit die Gesamtdosis durch interne Kontamination erheblich. Wenn eine radioaktive Verbindung mit radioaktiver Halbwertszeit (t _1/2 ) mit einer biologischen Halbwertszeit t _b aus dem Körper entfernt wird , wird die „effektive“ Halbwertszeit (t _e ) durch den Ausdruck gegeben:

Wie zu sehen ist, verringern die biologischen Mechanismen immer die Gesamtdosis aufgrund innerer Kontamination. Wenn außerdem t _1/2 im Vergleich zu t _b groß ist , ist die effektive Halbwertszeit ungefähr dieselbe wie t _b . Beispielsweise hat Tritium eine biologische Halbwertszeit von etwa 10 Tagen, während die radioaktive Halbwertszeit etwa 12 Jahre beträgt.

Siehe auch: Biologische Halbwertszeit

Siehe auch: Effektive Halbwertszeit

……………………………………………………………………………………………………………………………….

Was ist Radionuklid – Radioisotop – Definition

Juli 10, 2020 von Nick Connor

Es gibt Nuklide, die instabil und radioaktiv sind. Diese Nuklide werden als Radionuklide (radioaktive Nuklide) oder Radioisotope (radioaktive Isotope) bezeichnet. Strahlendosimetrie

In der Kernphysik und Kernchemie werden die verschiedenen Arten von Atomen, deren Kerne eine bestimmte Anzahl von Protonen und Neutronen enthalten, als Nuklide bezeichnet . Nuklide zeichnen sich auch durch ihre Kernenergiezustände aus (z. B. metastabiles Nuklid ^242m Am). Jedes Nuklid wird durch das chemische Symbol des Elements (dies gibt Z an) mit der Atommassenzahl als hochgestellt bezeichnet. Isotope sind Nuklide, die die gleiche Ordnungszahl und damit das gleiche Element haben, sich jedoch in der Anzahl der Neutronen unterscheiden.

Es gibt Nuklide, die instabil und radioaktiv sind. Diese Nuklide werden als Radionuklide (radioaktive Nuklide) oder Radioisotope (radioaktive Isotope) bezeichnet. Diese instabilen Isotope zerfallen auf verschiedenen Wegen des radioaktiven Zerfalls, am häufigsten durch Alpha-Zerfall, Beta-Zerfall, Gamma-Zerfall oder Elektroneneinfang. Viele andere seltene Zerfallsarten wie Spontanspaltung oder Neutronenemission sind bekannt.

Wie geschrieben wurde, den radioaktiven Zerfall der Radionuklide ist ein zufälliger Prozess auf der Ebene der einzelnen Atome, dass nach der Quantentheorie, es unmöglich ist , vorherzusagen , wann ein bestimmtes Atom zerfällt. Mit anderen Worten, ein Kern eines Radionuklids hat kein „Gedächtnis“. Ein Kern „altert“ nicht im Laufe der Zeit. Somit steigt die Wahrscheinlichkeit seines Zerfalls nicht mit der Zeit, sondern bleibt konstant, egal wie lange der Kern existiert hat.

Der Anteil der ursprünglichen Aktivität, der nach den folgenden Halbwertszeiten verbleibt, beträgt:

Aktivität nach 1 Halbwertszeit = ½ des Originals

Aktivität nach 2 Halbwertszeiten = ½ x ½ = ¼ des Originals

Aktivität nach 3 Halbwertszeiten = ½ x ½ x ½ = (½) ³ = 1/8 des Originals

Aktivität nach 4 Halbwertszeiten = (½) ⁴ = 1/16 des Originals

Aktivität nach 5 Halbwertszeiten = (½) ⁵ = 1/32 des Originals

Aktivität nach 6 Halbwertszeiten = (½) ⁶ = 1/64 des Originals

Aktivität nach 7 Halbwertszeiten = (½) ⁷ = 1/128 des Originals

Gesetz über den radioaktiven Zerfall: N = Ne- ^λt

Das Gesetz über den radioaktiven Zerfall kann auch für Aktivitätsberechnungen oder Massenberechnungen für radioaktives Material abgeleitet werden:

(Anzahl der Kerne) N = Ne- ^λt (Aktivität) A = Ae- ^λt (Masse) m = me- ^λt

Halbwertszeit und Radioaktivität von Radionukliden

Beispiel – Radioaktivität von Radionuklid

Eine Materialprobe enthält 1 Mikrogramm Jod-131. Beachten Sie, dass Jod-131 eine wichtige Rolle als radioaktives Isotop in Kernspaltungsprodukten spielt und einen wesentlichen Beitrag zu den Gesundheitsgefahren leistet, wenn es während eines Unfalls in die Atmosphäre freigesetzt wird. Jod-131 hat eine Halbwertszeit von 8,02 Tagen.

Berechnung:

Die Anzahl der anfänglich vorhandenen Iod-131-Atome.
Die Aktivität des Iod-131 in Curies.
Die Anzahl der Iod-131-Atome, die in 50 Tagen verbleiben.
Die Zeit, die die Aktivität benötigt, um 0,1 mCi zu erreichen.

Lösung:

Die Anzahl der Atome von Iod-131 kann unter Verwendung der Isotopenmasse wie folgt bestimmt werden.

N _I-131 = m _I-131 . N _A / M _I-131

N _I-131 = (1 & mgr; g ) x (6,02 × 10 ²³ Kerne / mol) / (130,91 g / mol)

N _I-131 = 4,6 × 10 ¹⁵ Kerne

Die Aktivität des Iod-131 in Curies kann anhand seiner Zerfallskonstante bestimmt werden :

Das Jod-131 hat eine Halbwertszeit von 8,02 Tagen (692928 Sekunden) und daher ist seine Zerfallskonstante:

Mit diesem Wert für die Abklingkonstante können wir die Aktivität der Probe bestimmen:

……………………………………………………………………………………………………………………………….

Was ist Röntgen – Röntgenstrahlung – Definition

Juli 6, 2021Juli 10, 2020 von Nick Connor

Unter Röntgenstrahlung , auch Röntgenstrahlung genannt , versteht man elektromagnetische Strahlung (keine Ruhemasse, keine Ladung) hoher Energien. Röntgenstrahlen sind energiereiche Photonen mit kurzen Wellenlängen und damit sehr hoher Frequenz. Die Strahlungsfrequenz ist der Schlüsselparameter aller Photonen, da sie die Energie eines Photons bestimmt. Photonen werden nach den Energien von energiearmen Radiowellen und Infrarotstrahlung über sichtbares Licht bis hin zu energiereichen Röntgen- und Gammastrahlen kategorisiert .

NASA - Elektromagnetisches Spektrum — Quelle: Rundgang durch das elektromagnetische Spektrum www.nasa.gov

Die meisten Röntgenstrahlen haben eine Wellenlänge im Bereich von 0,01 bis 10 Nanometer (3 × 10 ¹⁶ Hz bis 3 × 10 ¹⁹ Hz), was Energien im Bereich von 100 eV bis 100 keV entspricht. Röntgenwellenlängen sind kürzer als die von UV-Strahlen und typischerweise länger als die von Gammastrahlen. Die Unterscheidung zwischen Röntgen- und Gammastrahlen ist nicht so einfach und hat sich in den letzten Jahrzehnten geändert. Nach der derzeit gültigen Definition werden Röntgenstrahlen von Elektronen außerhalb des Kerns emittiert , während Gammastrahlen vom Kern emittiert werden .

Da die Röntgenstrahlen (insbesondere harte Röntgenstrahlen) im Wesentlichen energiereiche Photonen sind, sind sie sehr durchdringende Materie und daher biologisch gefährlich. Röntgenstrahlen können Tausende von Fuß in der Luft wandern und leicht durch den menschlichen Körper gelangen.

Entdeckung von Röntgenstrahlen – Wilhelm Conrad Röntgen

Röntgenentdeckung - Röntgen — Hand mit Ringen: Druck von Wilhelm Röntgens erstem „medizinischen“ Röntgenbild der Hand seiner Frau, aufgenommen am 22. Dezember 1895 und am 1. Januar 1896 an Ludwig Zehnder vom Physik Institut der Universität Freiburg übergeben.
Quelle : wikipedia.org Lizenz: Public Domain

Röntgenstrahlen wurden am 8. November 1895 von dem deutschen Physikprofessor Wilhelm Conrad Röntgen entdecktan der Universität Würtzburg in Deutschland. Er untersuchte elektrische Entladungen in Glasröhren, die mit verschiedenen Gasen bei sehr niedrigem Druck gefüllt waren. In diesen Experimenten hatte Röntgen die Röhre mit etwas schwarzem Papier bedeckt und den Raum abgedunkelt. Dann entdeckte er, dass ein mit einem fluoreszierenden Farbstoff bemaltes Stück Papier in einiger Entfernung von der Röhre glühen würde, wenn er die Hochspannung zwischen den Elektroden in der Röhre einschaltete. Er bemerkte, dass er ein zuvor unbekanntes „unsichtbares Licht“ oder einen Strahl erzeugt hatte, der aus der Röhre ausgestrahlt wurde, und einen Strahl, der in der Lage war, das schwere Papier, das die Röhre bedeckte, zu durchdringen. Röntgen bezeichnete die Strahlung als „X“, um anzuzeigen, dass es sich um eine unbekannte Art von Strahlung handelte.

Röntgen erkannte die Bedeutung seiner Entdeckung und konzentrierte sich ganz auf die Untersuchung dieser neuen Strahlung, die die ungewöhnliche Eigenschaft hatte, durch schwarzes Papier hindurchzugehen. Durch zusätzliche Experimente fand er auch heraus, dass der neue Strahl die meisten Substanzen durchdringen würde, die Schatten von festen Objekten wie Holzklötzen, Büchern und sogar seiner Hand werfen. Er fand heraus, dass sich Röntgenstrahlen in geraden Linien ausbreiten, von denen sie weder durch elektrische noch durch magnetische Felder abgelenkt werden. Das erste Röntgenbild war ein Bild der Hand seiner Frau auf einer durch Röntgenstrahlen entstandenen Fotoplatte. Seine Entdeckung breitete sich schnell auf der ganzen Welt aus und Wilhelm Conrad Röntgen erhielt für seine Entdeckung den ersten Nobelpreis für Physik.

Eigenschaften von Röntgenstrahlen

Die Hauptmerkmale von Röntgenstrahlen sind in folgenden Punkten zusammengefasst:

Röntgenstrahlen sind hochenergetische Photonen (etwa 100- bis 1000-mal so viel Energie wie die sichtbaren Photonen), die gleichen Photonen wie die Photonen, die den sichtbaren Bereich des elektromagnetischen Spektrums bilden – Licht.
Röntgenstrahlen werden üblicherweise durch ihre maximale Energie beschrieben, die durch die Spannung zwischen den Elektroden bestimmt wird. Sie kann von etwa 20 kV bis 300 kV reichen. Strahlung mit niedriger Spannung wird als “ weich “ bezeichnet – und Strahlung mit hoher Spannung wird als “ hart “ bezeichnet.
Photonen (Gammastrahlen und Röntgenstrahlen) können Atome durch den photoelektrischen Effekt und den Compton-Effekt direkt (obwohl sie elektrisch neutral sind) ionisieren, aber die sekundäre (indirekte) Ionisation ist viel bedeutender.
Röntgenstrahlen ionisieren Materie durch indirekte Ionisation .
Obwohl eine große Anzahl möglicher Wechselwirkungen bekannt ist, gibt es drei wichtige Wechselwirkungsmechanismen mit Materie.
- Photoelektrischer Effekt
- Compton-Streuung
- Rayleigh-Streuung
Röntgenstrahlen bewegen sich mit Lichtgeschwindigkeit und können Hunderte von Metern in der Luft zurücklegen, bevor sie ihre Energie verbrauchen.
Da die harten Röntgenstrahlen sehr durchdringende Materie sind, muss sie durch sehr dichte Materialien wie Blei oder Uran abgeschirmt werden.
Die Unterscheidung zwischen Röntgen- und Gammastrahlen ist nicht so einfach und hat sich in den letzten Jahrzehnten geändert. Nach der derzeit gültigen Definition werden Röntgenstrahlen von Elektronen außerhalb des Kerns emittiert , während Gammastrahlen vom Kern emittiert werden .
Für Röntgenstrahlen, die mit einer Röntgenröhre erzeugt werden, gibt es zwei verschiedene Arten von Röntgenspektren:
- Bremsstrahlung
- Charakteristische Röntgenstrahlen
Charakteristische Röntgenstrahlen begleiten häufig einige Arten von nuklearen Zerfällen, wie z. B. interne Umwandlung und Elektroneneinfang .

Röntgen – Produktion

Da Röntgenstrahlen hochenergetische Photonen sind , die elektromagnetischer Natur sind , können sie immer dann erzeugt werden, wenn geladene Teilchen (Elektronen oder Ionen) mit ausreichender Energie auf ein Material treffen. Es ähnelt dem photoelektrischen Effekt , bei dem Photonen vernichtet werden können, wenn sie auf die Metallplatte treffen, wobei jedes seine kinetische Energie an ein Elektron abgibt .

Röntgenstrahlen können durch eine Röntgenröhre erzeugt werden , eine Vakuumröhre, die eine hohe Spannung verwendet, um die von einer heißen Kathode freigesetzten Elektronen auf eine hohe Geschwindigkeit zu beschleunigen. Die Kathode muss erwärmt werden, um Elektronen zu emittieren. Elektronen, die durch Potentialdifferenzen von Zehntausenden von Volt beschleunigt werden, zielen auf ein Metalltarget (normalerweise aus Wolfram oder einem anderen Schwermetall) in einer Vakuumröhre. Je größer die Spannung zwischen den Elektroden ist, desto mehr Energie erreichen die Elektronen. Beim Auftreffen auf das Ziel werden die beschleunigten Elektronen abrupt gestoppt und Röntgenstrahlen abgegebenund Wärme werden erzeugt. Der größte Teil der Energie wird in der Anode in Wärme umgewandelt (die gekühlt werden muss). Nur 1% der kinetischen Energie der Elektronen wird in Röntgenstrahlen umgewandelt. Röntgenstrahlen werden normalerweise senkrecht zum Weg des Elektronenstrahls erzeugt.

Eine spezielle Röntgenquelle, die in der Forschung immer häufiger eingesetzt wird, ist der Teilchenbeschleuniger, der als Synchrotronstrahlung bekannte Strahlung erzeugt . Wenn sich ultra-relativistisch geladene Teilchen durch Magnetfelder bewegen, müssen sie sich auf einem gekrümmten Pfad bewegen. Da sich ihre Bewegungsrichtung ständig ändert, beschleunigen sie auch und emittieren so Bremsstrahlung, in diesem Fall wird sie als Synchrotronstrahlung bezeichnet .

Röntgenstrahlen können auch von schnellen Protonen oder anderen positiven Ionen erzeugt werden. Die protoneninduzierte Röntgenemission oder partikelinduzierte Röntgenemission wird häufig als Analyseverfahren verwendet.

Weiche und harte Röntgenstrahlen

Röntgenstrahlen werden normalerweise durch ihre maximale Energie beschrieben, die durch die Spannung zwischen den Elektroden bestimmt wird. Röntgenstrahlen mit hohen Photonenenergien (über 5–10 keV) werden als harte Röntgenstrahlen bezeichnet , während solche mit niedrigerer Energie (und längerer Wellenlänge) als weiche Röntgenstrahlen bezeichnet werden . Aufgrund ihrer Durchdringungsfähigkeit werden häufig harte Röntgenstrahlen verwendet, um das Innere von visuell undurchsichtigen Objekten abzubilden. Die am häufigsten gesehenen Anwendungen sind in der medizinischen Radiographie. Da die Wellenlängen harter Röntgenstrahlen der Größe von Atomen ähnlich sind, eignen sie sich auch zur Bestimmung von Kristallstrukturen durch Röntgenkristallographie. Im Gegensatz dazu werden weiche Röntgenstrahlen leicht von Luft absorbiert. Die Dämpfungslänge von 600 eV Röntgenstrahlen in Wasser beträgt weniger als 1 Mikrometer.

Röntgenspektrum – charakteristisch und kontinuierlich

Bei Röntgenstrahlen, die von einer Röntgenröhre erzeugt werden, variiert der Teil der Energie, der in Strahlung umgewandelt wird, von Null bis zur maximalen Energie des Elektrons, wenn es auf die Anode trifft. Die maximale Energie des erzeugten Röntgenphotons wird durch die Energie des einfallenden Elektrons begrenzt, die gleich der Spannung an der Röhre mal der Elektronenladung ist, sodass eine 100-kV-Röhre keine Röntgenstrahlen mit einer Energie von mehr als 100 erzeugen kann keV. Wenn die Elektronen auf das Ziel treffen, werden Röntgenstrahlen durch zwei verschiedene atomare Prozesse erzeugt:

Bremsstrahlung . Die Bremsstrahlung ist elektromagnetische Strahlung, die durch die Beschleunigung oder Verzögerung eines Elektrons erzeugt wird, wenn es durch starke elektromagnetische Felder von Zielkernen mit hohem Z (Protonenzahl) abgelenkt wird . Der Name Bremsstrahlung stammt aus dem Deutschen. Die wörtliche Übersetzung lautet „Bremsstrahlung“ . Nach der klassischen Theorie muss ein geladenes Teilchen, wenn es beschleunigt oder abgebremst wird, Energie ausstrahlen. Die Bremsstrahlung ist eine der möglichen Wechselwirkungen von lichtgeladenen Teilchen mit Materie (insbesondere mit hohen Atomzahlen)). Diese Röntgenstrahlen haben ein kontinuierliches Spektrum. Die Intensität der Röntgenstrahlen steigt linear mit abnehmender Frequenz von Null bei der Energie der einfallenden Elektronen, der Spannung an der Röntgenröhre. Das Ändern des Materials, aus dem das Target in der Röhre besteht, hat keinen Einfluss auf das Spektrum dieser kontinuierlichen Strahlung. Wenn wir beispielsweise von einem Molybdän-Target zu einem Kupfer-Target wechseln würden, würden sich alle Merkmale des Röntgenspektrums mit Ausnahme der Grenzwellenlänge ändern.
Charakteristische Röntgenemission. Wenn das Elektron genug Energie hat, kann es ein Orbitalelektron aus der inneren Elektronenhülle eines Metallatoms schlagen. Da der Prozess eine Lücke in dem Elektronenenergieniveau hinterlässt, aus dem das Elektron stammt, kaskadieren die äußeren Elektronen des Atoms nach unten , um die unteren Atomebenen zu füllen, und normalerweise werden eine oder mehrere charakteristische Röntgenstrahlen emittiert. Infolgedessen erscheinen scharfe Intensitätsspitzen im Spektrum bei Wellenlängen, die für das Material charakteristisch sind, aus dem das Anodentarget hergestellt ist. Die Frequenzen der charakteristischen Röntgenstrahlen können aus dem Bohr-Modell vorhergesagt werden.

Wechselwirkung von Röntgenstrahlen mit Materie

Obwohl eine große Anzahl möglicher Wechselwirkungen bekannt ist, gibt es drei wichtige Wechselwirkungsmechanismen mit Materie. Die Stärke dieser Wechselwirkungen hängt von der Energie der Röntgenstrahlen und der Elementzusammensetzung des Materials ab, jedoch nicht wesentlich von den chemischen Eigenschaften, da die Röntgenphotonenenergie viel höher ist als die chemischen Bindungsenergien. Die photoelektrische Absorption dominiert bei niedrigen Energien von Röntgenstrahlen, während die Compton-Streuung bei höheren Energien dominiert.

Photoelektrische Absorption
Compton-Streuung
Rayleigh-Streuung

Photoelektrische Absorption von Röntgenstrahlen

Gamma-Absorption durch ein Atom. Quelle: laradioactivite.com/ — Gamma-Absorption durch ein Atom.
Quelle: laradioactivite.com/

Beim photoelektrischen Effekt unterliegt ein Photon einer Wechselwirkung mit einem Elektron, das in einem Atom gebunden ist. Bei dieser Wechselwirkung verschwindet das einfallende Photon vollständig und ein energetisches Photoelektron wird vom Atom aus einer seiner gebundenen Schalen ausgestoßen . Die kinetische Energie des ausgestoßenen Photoelektron (E _e ) ist gleich der einfallenden Photonenenergie (hν) abzüglich der Bindungsenergie des Photoelektron in seiner ursprünglichen Hülle (E _b ).

E _e = hν-E _b

Daher werden Photoelektronen nur dann durch den photoelektrischen Effekt emittiert, wenn das Photon eine Schwellenenergie – die Bindungsenergie des Elektrons – die Austrittsarbeit des Materials erreicht oder überschreitet . Bei sehr hohen Röntgenstrahlen mit Energien von mehr als Hunderten keV trägt das Photoelektron den größten Teil der einfallenden Photonenenergie ab – hν.

Bei kleinen Werten der Gammastrahlenenergie dominiert der photoelektrische Effekt . Der Mechanismus wird auch für Materialien mit hoher Ordnungszahl Z verbessert. Es ist nicht einfach, einen analytischen Ausdruck für die Wahrscheinlichkeit der photoelektrischen Absorption von Gammastrahlen pro Atom über alle Bereiche von Gammastrahlenenergien abzuleiten. Die Wahrscheinlichkeit der photoelektrischen Absorption pro Masseneinheit ist ungefähr proportional zu:

τ _{(photoelektrisch)} = Konstante x Z ^N / E ^3.5

wobei Z die Ordnungszahl ist, variiert der Exponent n zwischen 4 und 5. E ist die Energie des einfallenden Photons. Die Proportionalität zu höheren Potenzen der Ordnungszahl Z ist der Hauptgrund für die Verwendung von Materialien mit hohem Z wie Blei oder abgereichertem Uran in Gammastrahlenschilden.

Obwohl die Wahrscheinlichkeit der photoelektrischen Absorption von Photonen im Allgemeinen mit zunehmender Photonenenergie abnimmt, gibt es scharfe Diskontinuitäten in der Querschnittskurve. Diese werden als „Absoptionskanten“ bezeichnet.und sie entsprechen den Bindungsenergien von Elektronen aus den gebundenen Schalen des Atoms. Für Photonen mit einer Energie knapp über dem Rand reicht die Photonenenergie gerade aus, um die photoelektrische Wechselwirkung mit Elektronen aus der gebundenen Schale, beispielsweise der K-Schale, einzugehen. Die Wahrscheinlichkeit einer solchen Wechselwirkung ist knapp über dieser Kante viel größer als die von Energiephotonen etwas unterhalb dieser Kante. Für Photonen unterhalb dieser Kante ist die Wechselwirkung mit Elektronen aus der K-Schale energetisch unmöglich und daher fällt die Wahrscheinlichkeit abrupt ab. Diese Kanten treten auch bei Bindungsenergien von Elektronen aus anderen Schalen (L, M, N… ..) auf.

Compton-Streuung von Röntgenstrahlen

Die Compton-Formel wurde 1923 in der Physical Review veröffentlicht. Compton erklärte , dass die X-ray Verschiebung von partikelartigen verursacht Impulse von Photonen . Die Compton-Streuungsformel ist die mathematische Beziehung zwischen der Verschiebung der Wellenlänge und dem Streuwinkel der Röntgenstrahlen. Bei der Compton-Streuung kollidiert das Photon der Frequenz f mit einem ruhenden Elektron. Bei einer Kollision prallt das Photon vom Elektron ab und gibt einen Teil seiner Anfangsenergie ab (gegeben durch die Plancksche Formel E = hf). Während das Elektron an Impuls gewinnt (Masse x Geschwindigkeit), kann das Photon seine Geschwindigkeit nicht senken. Aufgrund des Impulserhaltungsgesetzes muss das Photon seinen Impuls senken, der gegeben ist durch:

Die Abnahme des Photonenimpulses muss also in eine Abnahme der Frequenz (Zunahme der Wellenlänge Δλ = λ ‚- λ ) übersetzt werden. Die Verschiebung der Wellenlänge nahm mit dem Streuwinkel gemäß der Compton-Formel zu :

wobei λ die anfängliche Wellenlänge des Photons ist, λ ‚ die Wellenlänge nach der Streuung ist, h die Planck-Konstante = 6,626 × 10 ^–34 Js ist, m _e die Elektronenruhmasse (0,511 MeV) ist c die Lichtgeschwindigkeit ist Θ die Streuung ist Winkel. Die minimale Änderung der Wellenlänge ( λ ‚ – λ ) für das Photon tritt auf, wenn Θ = 0 ° (cos (Θ) = 1) und mindestens Null ist. Die maximale Änderung der Wellenlänge ( λ ′ – λ) für das Photon tritt auf, wenn Θ = 180 ° (cos (Θ) = – 1). In diesem Fall überträgt das Photon so viel Impuls wie möglich auf das Elektron. Die maximale Änderung der Wellenlänge kann aus der Compton-Formel abgeleitet werden:

Die Größe h / m _e c ist als Compton-Wellenlänge des Elektrons bekannt und beträgt 2,43 × 10 ^–12 m .

Rayleigh-Streuung – Thomson-Streuung

Rayleigh-Streuung , auch als Thomson-Streuung bekannt, ist die energiearme Grenze der Compton-Streuung. Die kinetische Energie der Teilchen und die Photonenfrequenz ändern sich infolge der Streuung nicht. Rayleigh-Streuung tritt als Ergebnis einer Wechselwirkung zwischen einem einfallenden Photon und einem Elektron auf, dessen Bindungsenergie signifikant größer ist als die des einfallenden Photons. Es wird angenommen, dass die einfallende Strahlung das Elektron in eine erzwungene Resonanzschwingung versetzt, so dass das Elektron Strahlung mit derselben Frequenz, jedoch in alle Richtungen, wieder emittiert. In diesem Fall beschleunigt das elektrische Feld der einfallenden Welle (Photon) das geladene Teilchen, wodurch es wiederum Strahlung mit der gleichen Frequenz wie die einfallende Welle emittiert und somit die Welle gestreut wird. Die Rayleigh-Streuung ist bis zu ≈ 20 keV signifikant und wie die Thomson-Streuung elastisch. Der Gesamtstreuquerschnitt wird zu einer Kombination der Rayleigh- und Compton-gebundenen Streuquerschnitte. Thomson-Streuung ist ein wichtiges Phänomen in der Plasmaphysik und wurde zuerst vom Physiker JJ Thomson erklärt. Diese Wechselwirkung hat im Bereich der Röntgenkristallographie eine große Bedeutung.

Röntgenschwächung

Wenn die hochenergetischen Photonen Material passieren, nimmt ihre Energie ab. Dies wird als Dämpfung bezeichnet . Die Dämpfungstheorie gilt auch für Röntgen- und Gammastrahlen . Es stellt sich heraus, dass Photonen mit höherer Energie (harte Röntgenstrahlen) leichter durch Gewebe wandern als Photonen mit niedriger Energie (dh Photonen mit höherer Energie interagieren weniger wahrscheinlich mit Materie). Ein Großteil dieses Effekts hängt mit dem photoelektrischen Effekt zusammen . Die Wahrscheinlichkeit einer photoelektrischen Absorption ist ungefähr proportional zu (Z / E) ³wobei Z die Ordnungszahl des Gewebeatoms und E die Photonenenergie ist. Wenn E größer wird, sinkt die Wahrscheinlichkeit einer Wechselwirkung schnell. Für höhere Energien wird die Compton-Streuung dominant. Die Compton-Streuung ist für verschiedene Energien ungefähr konstant, obwohl sie bei höheren Energien langsam abnimmt.

Siehe auch: Röntgenschwächung

Abschirmung von Röntgenstrahlen

Kurz gesagt basiert eine wirksame Abschirmung von Röntgenstrahlen in den meisten Fällen auf der Verwendung von Materialien mit zwei folgenden Materialeigenschaften:

hohe Materialdichte.
hohe Ordnungszahl des Materials (Materialien mit hohem Z)

Ein Blei wird häufig als Röntgenschutz verwendet . Der Hauptvorteil des Bleischildes liegt in seiner Kompaktheit aufgrund seiner höheren Dichte. Ein Blei wird häufig als Gammaschild verwendet. Auf der anderen Seite ist abgereichertes Uran aufgrund seines höheren Z viel effektiver. Abgereichertes Uran wird zur Abschirmung in tragbaren Gammastrahlenquellen verwendet.

Im Allgemeinen ist die Röntgenabschirmung komplexer und schwieriger als die Alpha- oder Betastrahlungsabschirmung . Um umfassend zu verstehen, wie ein Röntgenstrahl seine Anfangsenergie verliert, wie er abgeschwächt und wie er abgeschirmt werden kann, müssen wir seine Interaktionsmechanismen genau kennen.

Siehe auch mehr Theorie: Wechselwirkung von Röntgenstrahlen mit Materie

Siehe auch Rechner: Gamma-Aktivität zur Dosisleistung (mit / ohne Schild)

Siehe auch XCOM – Photonenquerschnittsdatenbank: XCOM: Photonenquerschnittsdatenbank

……………………………………………………………………………………………………………………………….