3-A-Regel – Abstand – Aufenthalt – Abschirmung
Im praktischen Strahlenschutz gibt es eine einfache Regel, um die Personendosis beruflich strahlenexponierter Personen möglichst niedrig zu halten. Die 3-A-Regel ist die Grundregel des Strahlenschutzes. Es besteht aus Abstand – Aufenthalt – Abschirmung.
- Aufenthalt. Die Höhe der Strahlenexposition hängt direkt (linear) von der Zeit ab, die Menschen in der Nähe der Strahlungsquelle verbringen. Die Dosis kann durch Begrenzung der Expositionszeit reduziert werden .
- Abstand. Die Höhe der Strahlenexposition hängt von dem Abstand von der Strahlung ab. Ähnlich wie bei einer Hitze von einem Feuer ist die Intensität der Wärmestrahlung hoch, wenn Sie zu nahe sind, und Sie können sich verbrennen. Wenn Sie in der richtigen Entfernung sind, können Sie dort problemlos standhalten und es ist außerdem bequem. Wenn Sie zu weit von der Wärmequelle entfernt sind, kann Sie auch die Unzulänglichkeit der Wärme verletzen. Diese Analogie kann in gewissem Sinne auch auf Strahlung von Strahlungsquellen angewendet werden.
- Abschirmung. Wenn die Quelle zu intensiv ist und Zeit oder Entfernung keinen ausreichenden Strahlenschutz bieten, muss die Abschirmung verwendet werden. Strahlenschutz besteht normalerweise aus Barrieren aus Blei, Beton oder Wasser. Es gibt viele verschiedene Materialien, die zur Strahlenabschirmung verwendet werden können, aber es gibt viele verschiedene Situationen beim Strahlenschutz. Dies hängt stark von der Art der abzuschirmenden Strahlung, ihrer Energie und vielen anderen Parametern ab. Zum Beispiel kann sogar abgereichertes Uran als guter Schutz vor Gammastrahlung verwendet werden, andererseits ist Uran eine absolut ungeeignete Abschirmung von Neutronenstrahlung.
Eigenschaften von Gammastrahlen / Strahlung
Die Hauptmerkmale von Gammastrahlen sind in folgenden Punkten zusammengefasst:
- Gammastrahlen sind hochenergetische Photonen (etwa 10 000-mal so viel Energie wie die sichtbaren Photonen), die gleichen Photonen wie die Photonen, die den sichtbaren Bereich des elektromagnetischen Spektrums bilden – Licht.
- Photonen (Gammastrahlen und Röntgenstrahlen) können Atome durch den photoelektrischen Effekt und den Compton-Effekt direkt (obwohl sie elektrisch neutral sind) ionisieren, aber die sekundäre (indirekte) Ionisation ist viel bedeutender.
- Gammastrahlen ionisieren Materie hauptsächlich durch indirekte Ionisation .
- Obwohl eine große Anzahl möglicher Wechselwirkungen bekannt ist, gibt es drei wichtige Wechselwirkungsmechanismen mit Materie.
- Gammastrahlen bewegen sich mit Lichtgeschwindigkeit und können Tausende von Metern in der Luft zurücklegen, bevor sie ihre Energie verbrauchen.
- Da die Gammastrahlung sehr durchdringende Materie ist, muss sie durch sehr dichte Materialien wie Blei oder Uran abgeschirmt werden.
- Die Unterscheidung zwischen Röntgen- und Gammastrahlen ist nicht so einfach und hat sich in den letzten Jahrzehnten geändert. Nach der derzeit gültigen Definition werden Röntgenstrahlen von Elektronen außerhalb des Kerns emittiert , während Gammastrahlen vom Kern emittiert werden .
- Gammastrahlen begleiten häufig die Emission von Alpha- und Betastrahlung .

Quelle: Wikimedia Commons
Abschirmung gegen Gammastrahlung
Kurz gesagt basiert eine wirksame Abschirmung der Gammastrahlung in den meisten Fällen auf der Verwendung von Materialien mit zwei folgenden Materialeigenschaften:
- hohe Materialdichte.
- hohe Ordnungszahl des Materials (Materialien mit hohem Z)
Materialien mit niedriger Dichte und Materialien mit niedrigem Z können jedoch mit einer erhöhten Dicke kompensiert werden, die bei Abschirmanwendungen ebenso wichtig ist wie Dichte und Ordnungszahl.
Ein Blei wird häufig als Gammaschild verwendet. Der Hauptvorteil des Bleischildes liegt in seiner Kompaktheit aufgrund seiner höheren Dichte. Auf der anderen Seite ist abgereichertes Uran aufgrund seines höheren Z viel effektiver. Abgereichertes Uran wird zur Abschirmung in tragbaren Gammastrahlenquellen verwendet.
In Kernkraftwerken kann die Abschirmung eines Reaktorkerns durch Materialien des Reaktordruckbehälters, Reaktoreinbauten ( Neutronenreflektor ) erfolgen. Auch schwerer Beton wird normalerweise verwendet, um sowohl Neutronen als auch Gammastrahlung abzuschirmen .
Obwohl Wasser weder ein Material mit hoher Dichte noch mit hohem Z-Gehalt ist, wird es üblicherweise als Gammaschutz verwendet. Wasser bietet eine Strahlenabschirmung von Brennelementen in einem Pool abgebrannter Brennelemente während der Lagerung oder während des Transports vom und in den Reaktorkern .
Im Allgemeinen ist die Abschirmung der Gammastrahlung komplexer und schwieriger als die Abschirmung der Alpha- oder Betastrahlung . Um umfassend zu verstehen, wie ein Gammastrahl seine Anfangsenergie verliert, wie er abgeschwächt und abgeschirmt werden kann, müssen wir seine Interaktionsmechanismen genau kennen.
Siehe auch mehr Theorie: Wechselwirkung von Gammastrahlung mit Materie
Siehe auch Rechner: Gamma-Aktivität zur Dosisleistung (mit / ohne Schild)
Siehe auch XCOM – Photonenquerschnittsdatenbank: XCOM: Photonenquerschnittsdatenbank
Gammastrahlenabschwächung
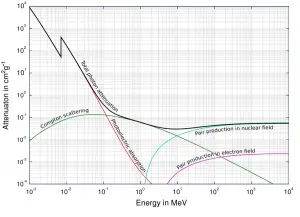
Der Gesamtquerschnitt der Wechselwirkung von Gammastrahlen mit einem Atom ist gleich der Summe aller drei genannten Teilquerschnitte: σ = σ f + σ C + σ p
- σ f – Photoelektrischer Effekt
- σ C – Compton-Effekt
- σ p – Paarbildung
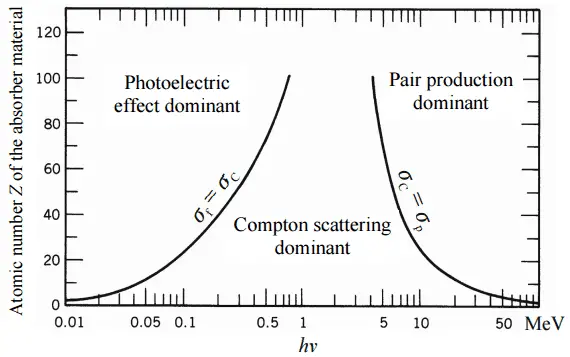
Abhängig von der Gammastrahlenenergie und dem Absorbermaterial kann einer der drei Teilquerschnitte viel größer werden als die beiden anderen. Bei kleinen Werten der Gammastrahlenenergie dominiert der photoelektrische Effekt . Bei Zwischenenergien dominiert die Compton-Streuung . Die Compton-Streuung nimmt auch mit abnehmender Ordnungszahl der Materie zu, daher ist das Dominanzintervall für Lichtkerne breiter. Schließlich dominiert die Produktion von Elektronen-Positronen-Paaren bei hohen Energien.
Basierend auf der Definition des Wechselwirkungsquerschnitts kann die Abhängigkeit der Intensität der Gammastrahlen von der Dicke des Absorbermaterials abgeleitet werden. Wenn monoenergetische Gammastrahlen zu einem schmalen Strahl kollimiert werden und der Detektor hinter dem Material nur die Gammastrahlen erfasst, die durch dieses Material hindurchgegangen sind, ohne dass eine Wechselwirkung mit diesem Material besteht, sollte die Abhängigkeit eine einfache exponentielle Abschwächung der Gammastrahlen sein . Jede dieser Wechselwirkungen entfernt das Photon entweder durch Absorption oder durch Streuung von der Detektorrichtung weg vom Strahl. Daher können die Wechselwirkungen durch eine feste Eintrittswahrscheinlichkeit pro Einheit Pfadlänge im Absorber charakterisiert werden. Die Summe dieser Wahrscheinlichkeiten heißt Absorptionskoeffizient:
μ = τ (photoelektrisch) + σ (Compton) + κ (Paar)
Absorptionskoeffizient
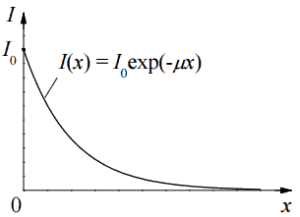
Die Dämpfung der Gammastrahlung kann dann durch die folgende Gleichung beschrieben werden.
I = I 0 .e -μx
wobei I die Intensität nach der Dämpfung ist, I o die Einfallsintensität ist, μ der Absorptionskoeffizient (cm –1 ) und die physikalische Dicke des Absorbers (cm) ist.
Die in der nebenstehenden Tabelle aufgeführten Materialien sind Luft, Wasser und verschiedene Elemente von Kohlenstoff ( Z = 6) bis Blei ( Z = 82). Ihre linearen Dämpfungskoeffizienten sind für drei Gammastrahlenenergien angegeben. Es gibt zwei Hauptmerkmale des Absorptionskoeffizienten:
- Der lineare Dämpfungskoeffizient nimmt mit zunehmender Ordnungszahl des Absorbers zu.
- Der lineare Dämpfungskoeffizient für alle Materialien nimmt mit der Energie der Gammastrahlen ab.
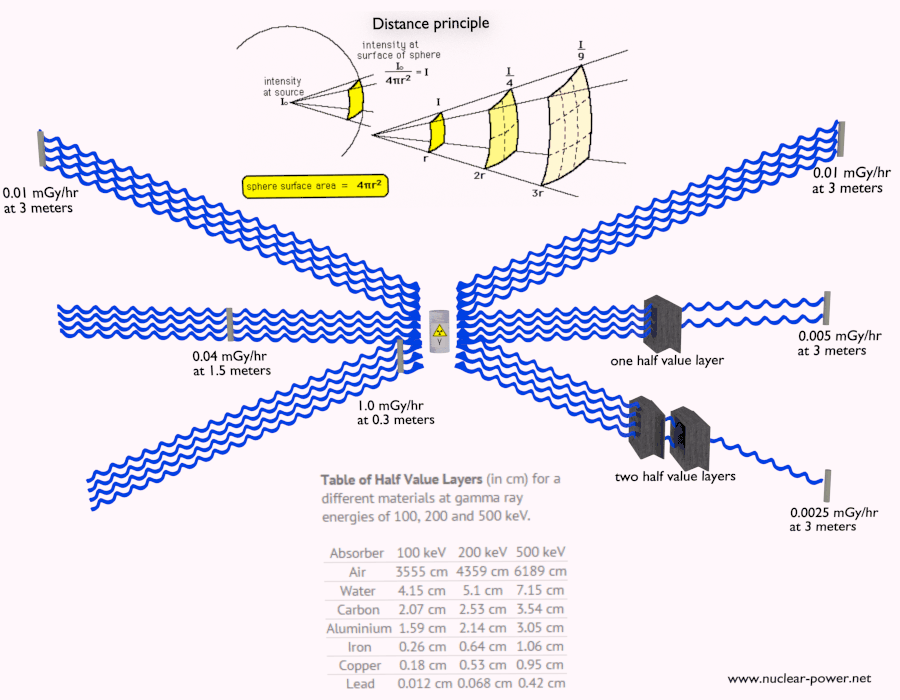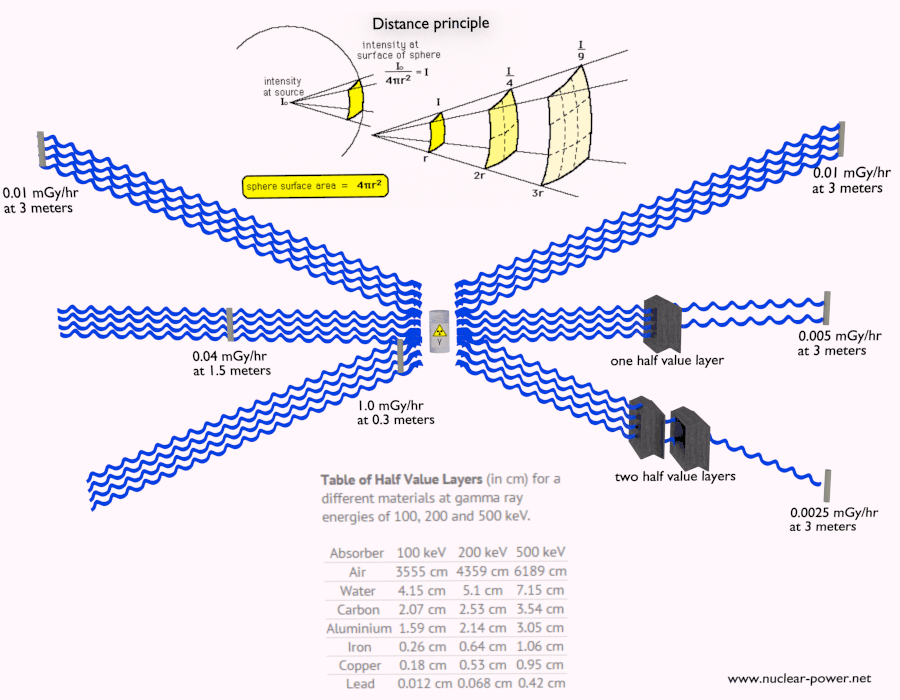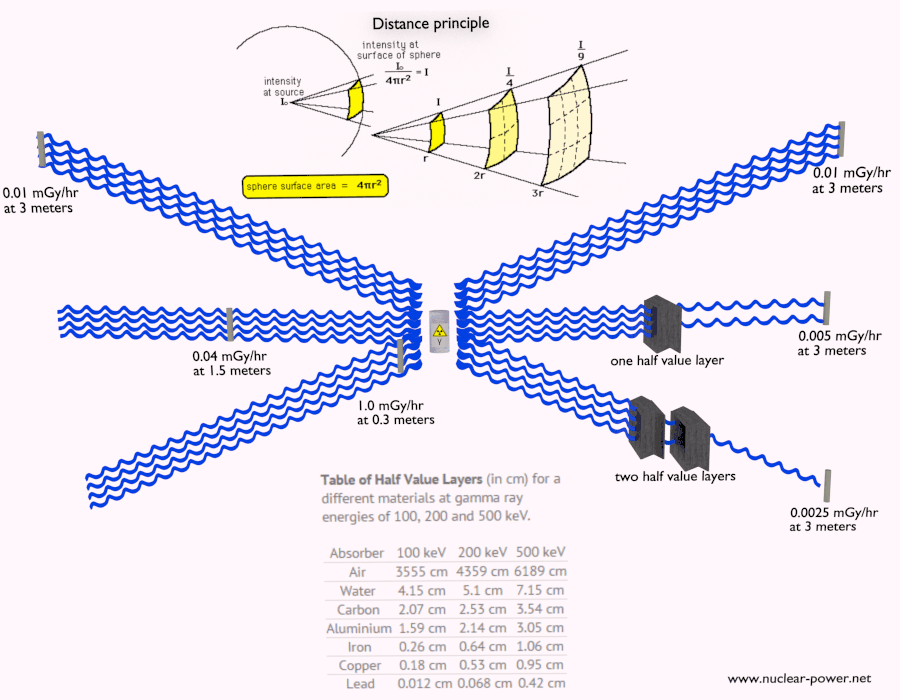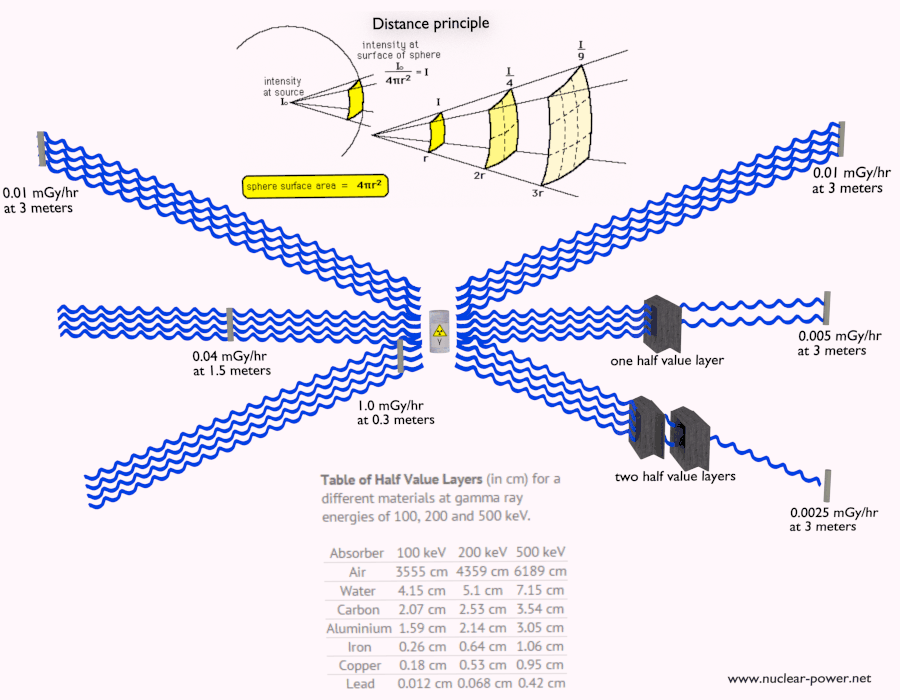
Halbwertsschicht
Die Halbwertsschicht drückt die Dicke des absorbierenden Materials aus, die zur Verringerung der Intensität der einfallenden Strahlung um den Faktor zwei benötigt wird . Es gibt zwei Hauptmerkmale der Halbwertsschicht:
- Die Halbwertsschicht nimmt mit zunehmender Ordnungszahl des Absorbers ab. Zum Beispiel werden 35 m Luft benötigt, um die Intensität eines 100-keV-Gammastrahls um den Faktor zwei zu verringern, während nur 0,12 mm Blei dasselbe bewirken können.
- Die Halbwertsschicht für alle Materialien nimmt mit der Energie der Gammastrahlen zu. Zum Beispiel von 0,26 cm für Eisen bei 100 keV bis etwa 1,06 cm bei 500 keV.
Beispiel:
Wie viel Wasserschutz benötigen Sie, wenn Sie die Intensität eines monoenergetischen 500-keV- Gammastrahls ( schmaler Strahl ) auf 1% seiner Einfallsintensität reduzieren möchten ? Die Halbwertsschicht für 500 keV Gammastrahlen in Wasser beträgt 7,15 cm und der lineare Dämpfungskoeffizient für 500 keV Gammastrahlen in Wasser beträgt 0,097 cm -1 . Die Frage ist recht einfach und kann durch folgende Gleichung beschrieben werden:Wenn die Halbwertsschicht für Wasser 7,15 cm beträgt, beträgt der lineare Dämpfungskoeffizient:
Jetzt können wir die exponentielle Dämpfungsgleichung verwenden:
deshalb
Die erforderliche Wasserdicke beträgt also ca. 47,5 cm . Dies ist eine relativ große Dicke und wird durch kleine Atomzahlen von Wasserstoff und Sauerstoff verursacht. Wenn wir das gleiche Problem für Blei (Pb) berechnen , erhalten wir die Dicke x = 2,8 cm .
Lineare Dämpfungskoeffizienten
Tabelle der Absorptionskoeffizienten (in cm & supmin ; ¹ ) für verschiedene Materialien bei Gammastrahlenenergien von 100, 200 und 500 keV.
| Absorber | 100 keV | 200 keV | 500 keV |
| Luft | 0,000195 / cm | 0,000159 / cm | 0,000112 / cm |
| Wasser | 0,167 / cm | 0,136 / cm | 0,097 / cm |
| Kohlenstoff | 0,335 / cm | 0,274 / cm | 0,196 / cm |
| Aluminium | 0,435 / cm | 0,324 / cm | 0,227 / cm |
| Eisen | 2,72 / cm | 1,09 / cm | 0,655 / cm |
| Kupfer | 3,8 / cm | 1,309 / cm | 0,73 / cm |
| Führen | 59,7 / cm | 10,15 / cm | 1,64 / cm |
Halbe Wertebenen
Die Halbwertsschicht drückt die Dicke des absorbierenden Materials aus, die zur Verringerung der Intensität der einfallenden Strahlung um den Faktor zwei benötigt wird. Mit der Halbwertsschicht ist es einfach, einfache Berechnungen durchzuführen.
Quelle: www.nde-ed.org
Tabelle der Halbwertsschichten (in cm) für verschiedene Materialien bei Gammastrahlenenergien von 100, 200 und 500 keV.
| Absorber | 100 keV | 200 keV | 500 keV |
| Luft | 3555 cm | 4359 cm | 6189 cm |
| Wasser | 4,15 cm | 5,1 cm | 7,15 cm |
| Kohlenstoff | 2,07 cm | 2,53 cm | 3,54 cm |
| Aluminium | 1,59 cm | 2,14 cm | 3,05 cm |
| Eisen | 0,26 cm | 0,64 cm | 1,06 cm |
| Kupfer | 0,18 cm | 0,53 cm | 0,95 cm |
| Führen | 0,012 cm | 0,068 cm | 0,42 cm |
Massendämpfungskoeffizient
Bei der Charakterisierung eines absorbierenden Materials können wir manchmal den Massendämpfungskoeffizienten verwenden. Der Massendämpfungskoeffizient ist definiert als das Verhältnis des linearen Dämpfungskoeffizienten und der Absorberdichte (μ / ρ) . Die Dämpfung der Gammastrahlung kann dann durch die folgende Gleichung beschrieben werden:
I = I 0 .e – (μ / ρ) .ρl
wobei ρ die Materialdichte ist, (μ / ρ) der Massendämpfungskoeffizient ist und ρ.l die Massendicke ist. Die Maßeinheit für den Massendämpfungskoeffizienten cm 2 g -1 .
Für Zwischenenergien dominiert die Compton-Streuung und verschiedene Absorber haben ungefähr gleiche Massendämpfungskoeffizienten. Dies liegt an der Tatsache, dass der Querschnitt der Compton-Streuung proportional zum Z (Ordnungszahl) ist und daher der Koeffizient proportional zur Materialdichte ρ ist. Bei kleinen Werten der Gammastrahlenenergie oder bei hohen Werten der Gammastrahlenenergie, bei denen der Koeffizient proportional zu höheren Potenzen der Ordnungszahl Z ist (für den photoelektrischen Effekt σ f ~ Z 5 ; für die Paarproduktion σ p ~ Z 2 ), wird die Der Dämpfungskoeffizient μ ist keine Konstante.
Gültigkeit des Exponentialgesetzes
Das Exponentialgesetz beschreibt immer die Dämpfung der Primärstrahlung durch Materie. Wenn Sekundärteilchen erzeugt werden oder wenn die Primärstrahlung ihre Energie oder Richtung ändert, ist die effektive Dämpfung viel geringer. Die Strahlung dringt tiefer in die Materie ein, als es das Exponentialgesetz allein vorschreibt. Der Prozess muss bei der Bewertung der Wirkung der Strahlenabschirmung berücksichtigt werden.
Aufbaufaktoren für die Abschirmung von Gammastrahlen
Der Aufbaufaktor ist ein Korrekturfaktor, der den Einfluss der gestreuten Strahlung plus aller Sekundärteilchen im Medium bei Abschirmungsberechnungen berücksichtigt. Wenn wir den Aufbau von Sekundärstrahlung berücksichtigen wollen, müssen wir den Aufbaufaktor einbeziehen . Der Aufbaufaktor ist dann ein multiplikativer Faktor, der die Reaktion auf die nicht kollidierten Photonen berücksichtigt, um den Beitrag der gestreuten Photonen einzuschließen. Somit kann der Aufbaufaktor als Verhältnis der Gesamtdosis zur Reaktion auf die nicht kollidierte Dosis erhalten werden.
Die erweiterte Formel für die Berechnung der Dosisleistung lautet:
Der ANSI / ANS-6.4.3-1991-Gammastrahlen-Dämpfungskoeffizienten und Aufbaufaktoren für technische Materialien enthält abgeleitete Gammastrahlen-Dämpfungskoeffizienten und Aufbaufaktoren für ausgewählte technische Materialien und Elemente zur Verwendung bei Abschirmungsberechnungen (ANSI / ANS-6.1) .1, 1991).
