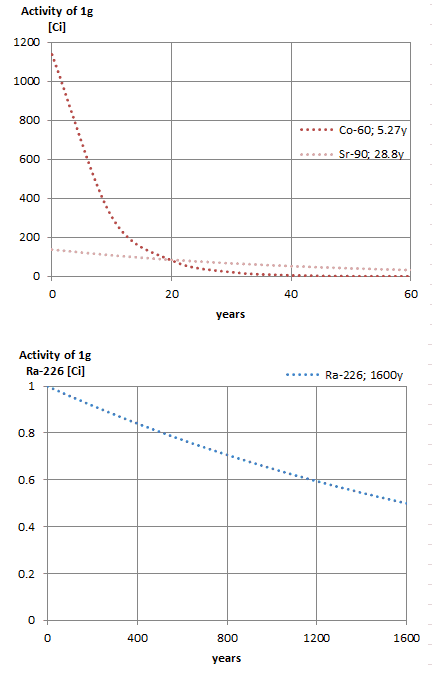
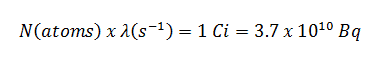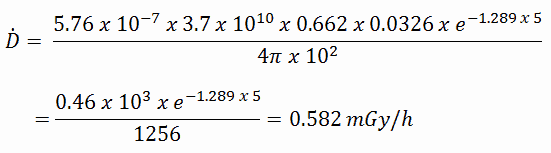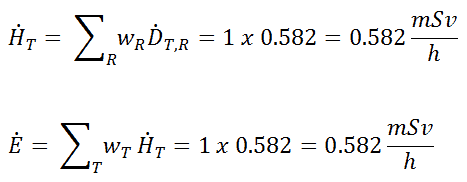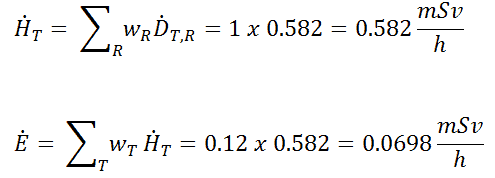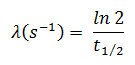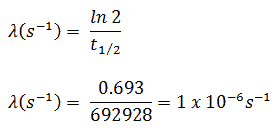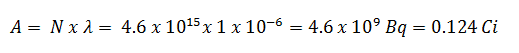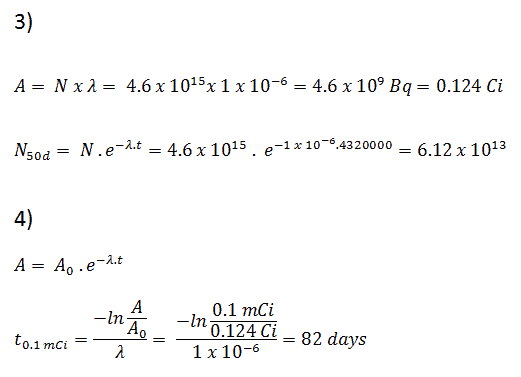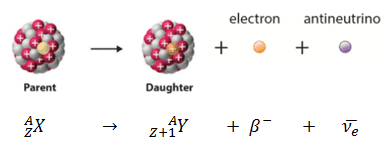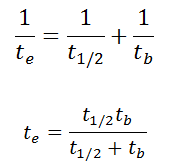- Limiter le temps. La quantité d’exposition aux rayonnements dépend directement (linéairement) du temps que les gens passent près de la source de rayonnement. La dose peut être réduite en limitant le temps d’exposition .
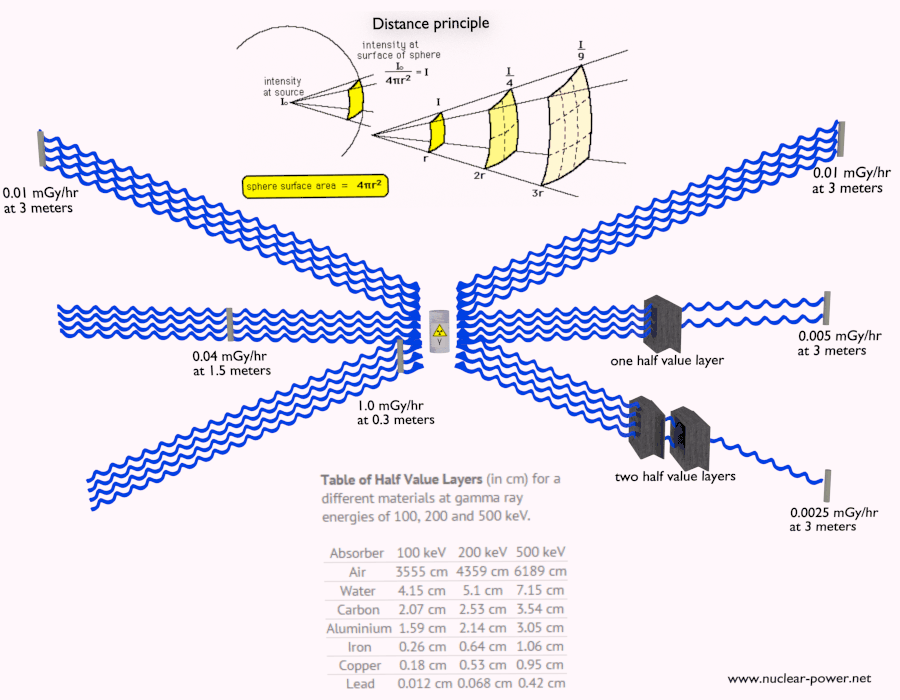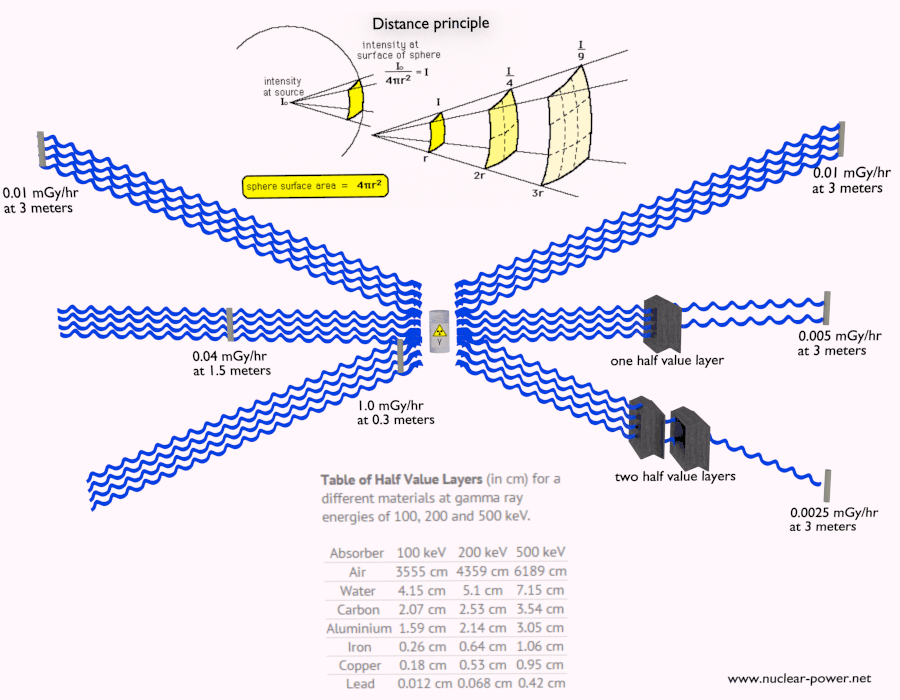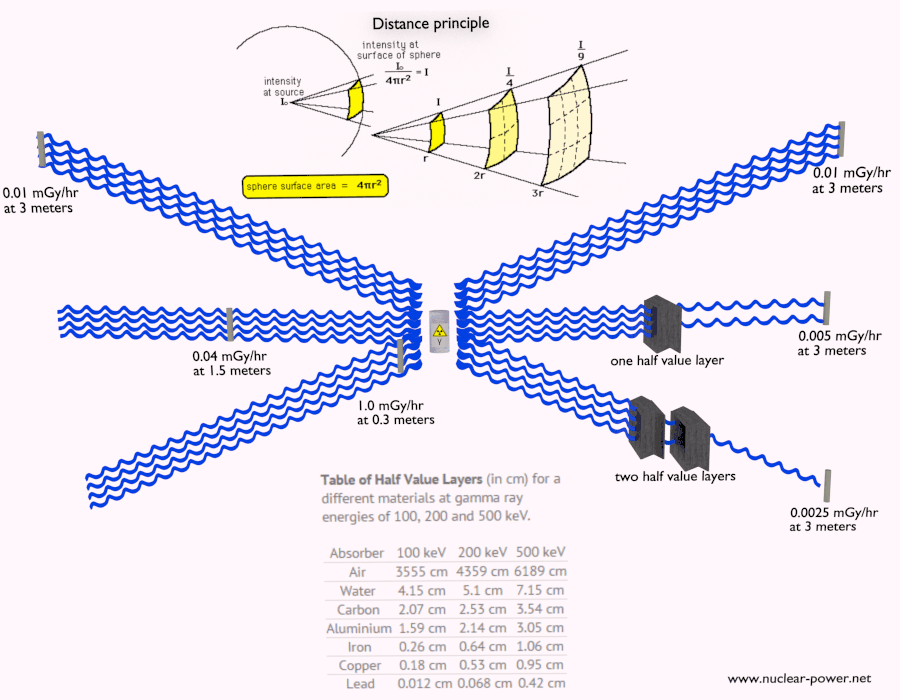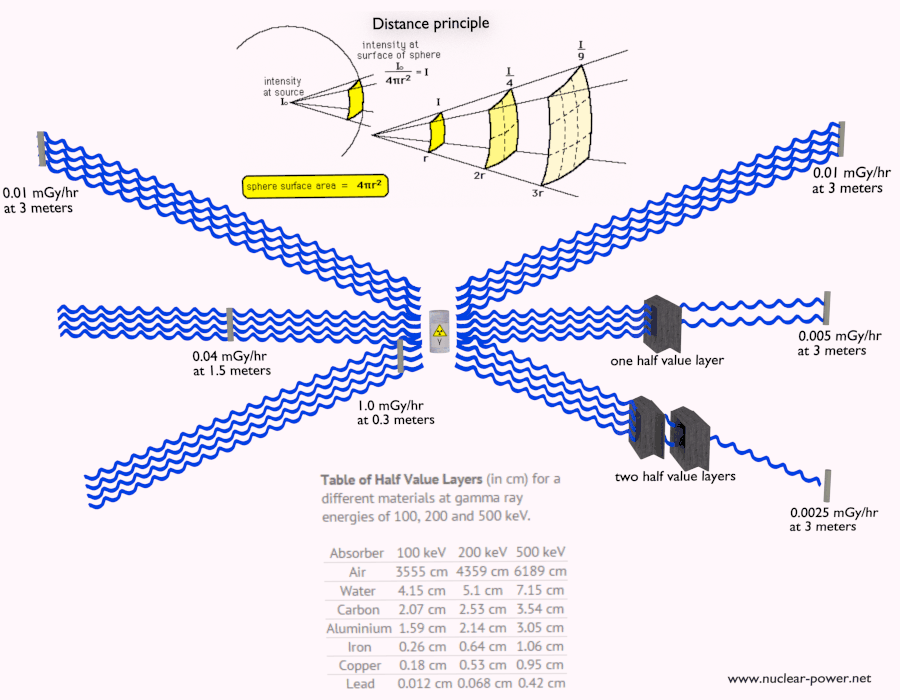
- Distance. La quantité d’exposition au rayonnement dépend de la distance de la source de rayonnement. Comme pour la chaleur d’un feu, si vous êtes trop près, l’intensité du rayonnement thermique est élevée et vous pouvez vous brûler. Si vous êtes à la bonne distance, vous pouvez y résister sans aucun problème et en plus c’est confortable. Si vous êtes trop loin d’une source de chaleur, l’insuffisance de chaleur peut également vous blesser. Cette analogie, dans un certain sens, peut être appliquée au rayonnement provenant également de sources de rayonnement.
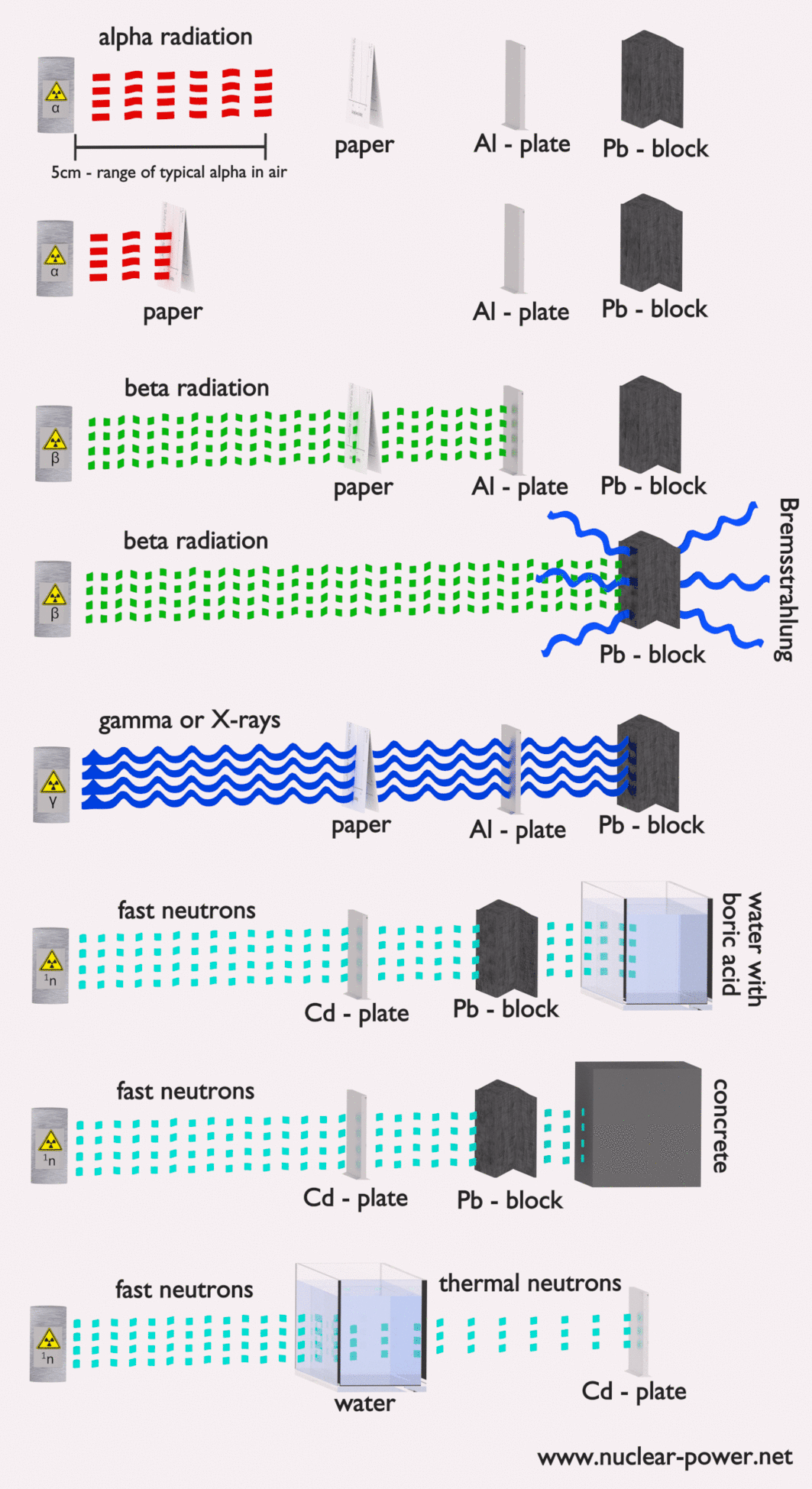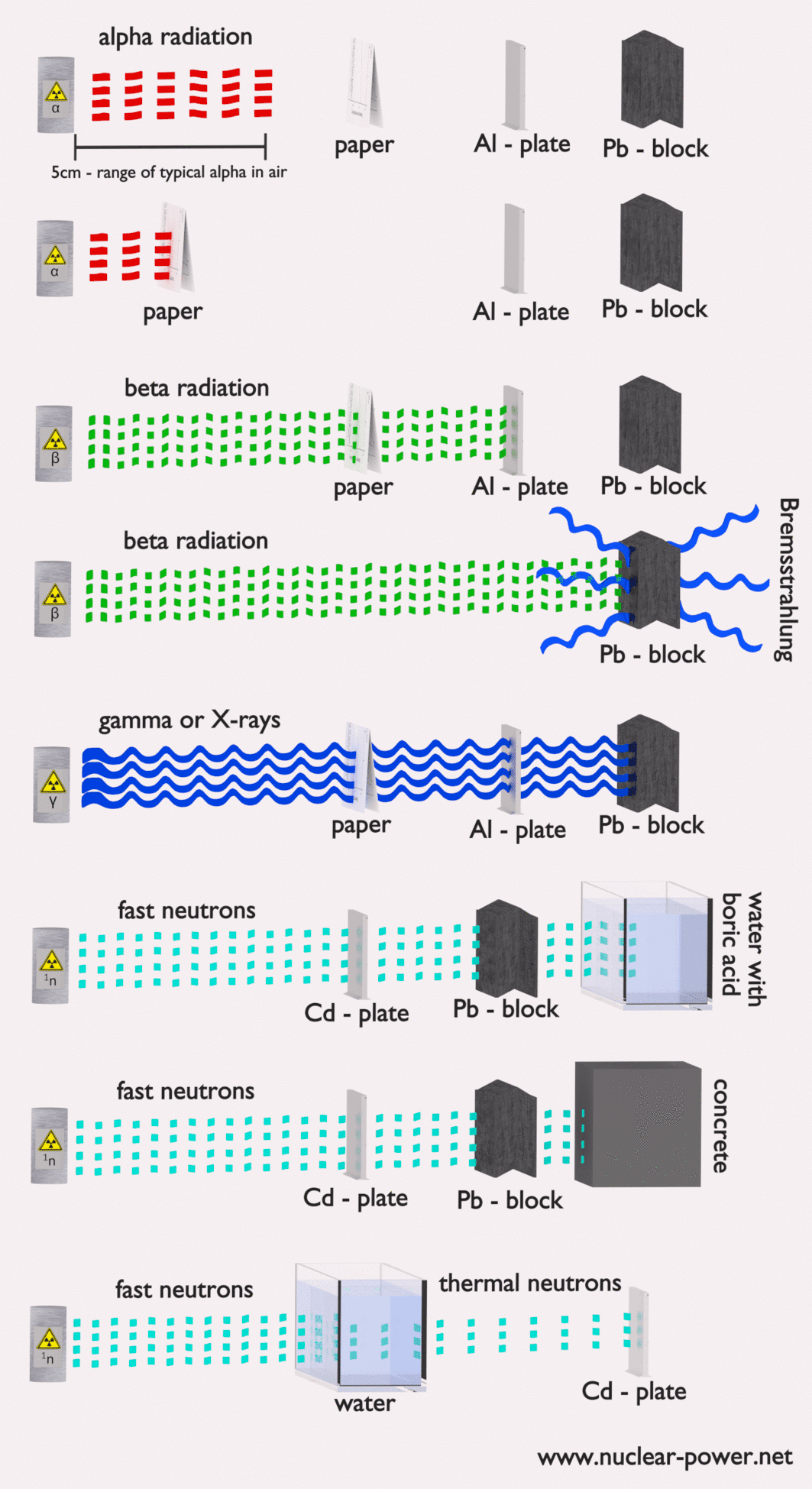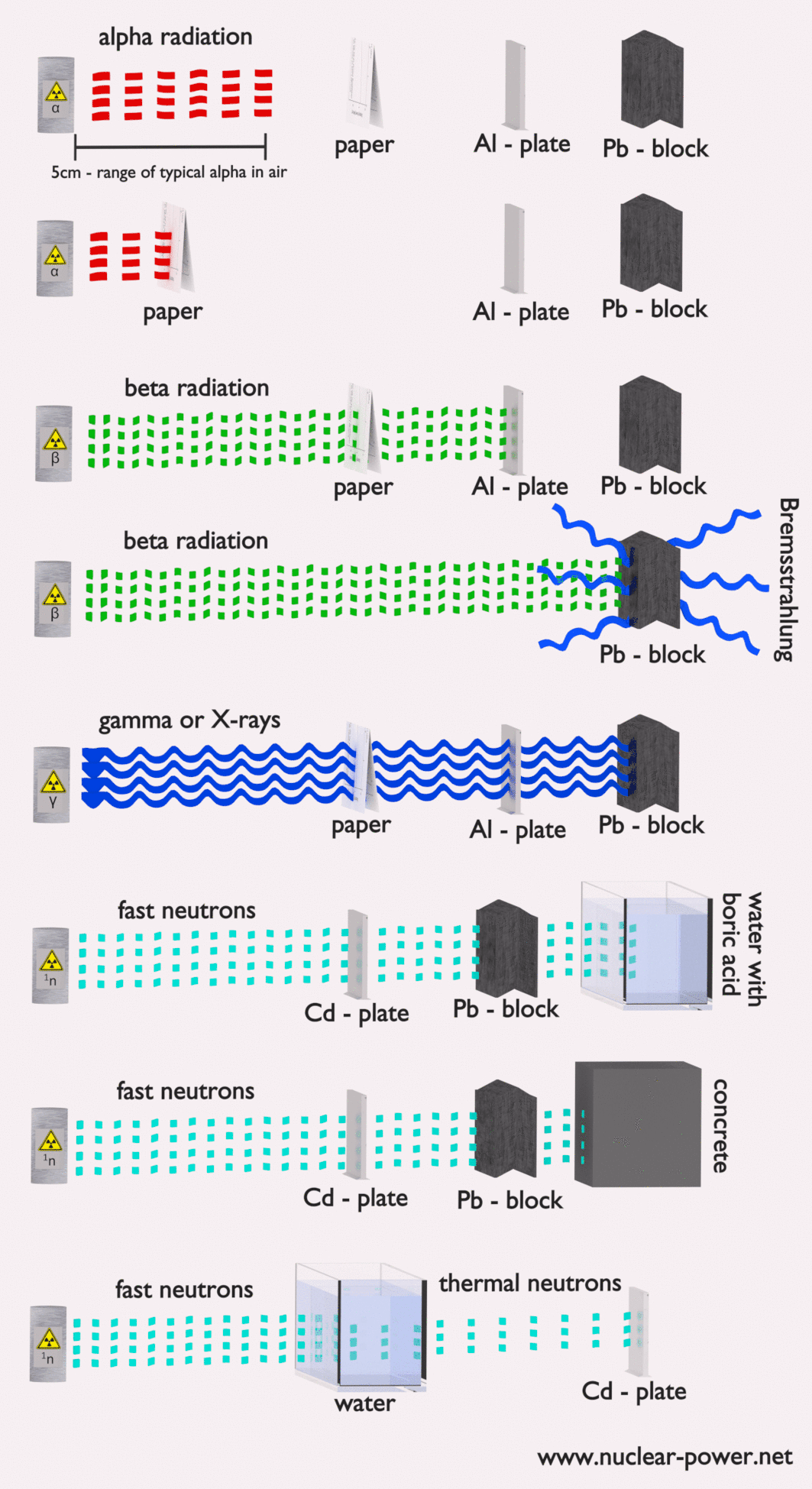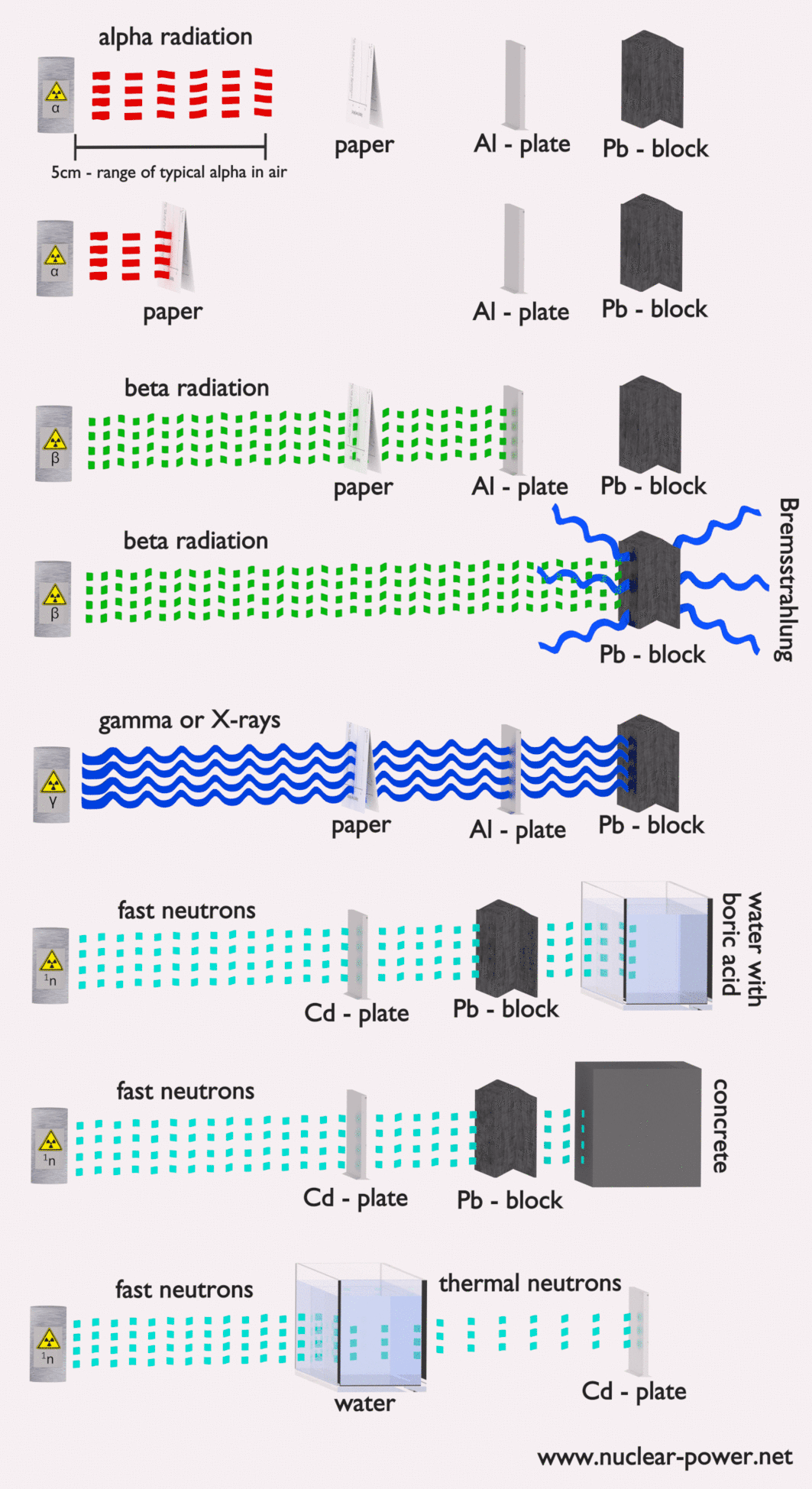
- Blindage. Enfin, si la source est trop intensive et que le temps ou la distance n’assurent pas une radioprotection suffisante, le blindage doit être utilisé. Le blindage contre les radiations est généralement composé de barrières de plomb, de béton ou d’eau. Il existe de nombreux matériaux qui peuvent être utilisés pour la protection contre les radiations, mais il existe de nombreuses situations dans la radioprotection. Cela dépend fortement du type de rayonnement à protéger, de son énergie et de nombreux autres paramètres. Par exemple, même l’uranium appauvri peut être utilisé comme une bonne protection contre le rayonnement gamma, mais d’un autre côté, l’uranium est un blindage absolument inapproprié du rayonnement neutronique .
- Type de rayonnement ionisant à protéger
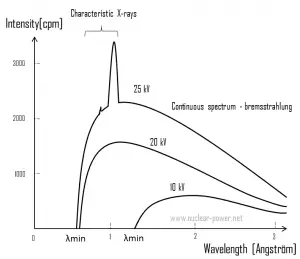
- Spectre énergétique du rayonnement ionisant
- Durée d’exposition
- Distance de la source du rayonnement ionisant
- Exigences relatives à l’atténuation du rayonnement ionisant – principes ALARA ou ALARP
- Degré de liberté de conception
- Autres exigences physiques (par exemple transparence dans le cas d’écrans en verre au plomb)
Voir aussi: Interaction du rayonnement avec la matière
Voir aussi: Rad Pro Calculator
Blindage des rayonnements dans les centrales nucléaires
Généralement, dans l’industrie nucléaire, le blindage contre les radiations a de nombreux objectifs. Dans les centrales nucléaires, l’objectif principal est de réduire l’exposition aux rayonnements des personnes et du personnel à proximité des sources de rayonnement. Dans les centrales nucléaires, la principale source de rayonnement est sans aucun doute le réacteur nucléaire et son cœur de réacteur . Les réacteurs nucléaires sont en général des sources puissantes de tout un spectre de types de rayonnements ionisants . Le blindage utilisé à cet effet est appelé blindage biologique .
Mais ce n’est pas le seul objectif du blindage contre les radiations. Des boucliers sont également utilisés dans certains réacteurs pour réduire l’intensité des rayons gamma ou des neutrons incidents sur la cuve du réacteur. Ce blindage contre les rayonnements protège la cuve du réacteur et ses composants internes (par exemple, le barillet de support du cœur ) contre le chauffage excessif dû à la modération rapide des neutrons par absorption des rayons gamma . Ces écrans sont généralement appelés écrans thermiques .
Voir aussi: Réflecteur à neutrons
Un blindage contre les radiations un peu étrange est généralement utilisé pour protéger le matériau de la cuve sous pression du réacteur (en particulier dans les centrales électriques REP ). Les matériaux de structure des réservoirs sous pression et les composants internes des réacteurs sont endommagés, en particulier par les neutrons rapides . Les neutrons rapides créent des défauts structurels, qui conduisent à la fragilisation du matériau du récipient sous pression . Afin de minimiser le flux de neutrons à la paroi du vaisseau, la stratégie de chargement du cœur peut également être modifiée. Dans la stratégie de chargement de combustible «à l’extérieur», des assemblages de combustible frais sont placés à la périphérie du cœur. Cette configuration entraîne une fluence neutronique élevée à la paroi du vaisseau. Par conséquent, la stratégie de chargement de carburant «in-out» (avec des modèles de chargement à faible fuite – L3P) a été adopté dans de nombreuses centrales nucléaires. Contrairement à la stratégie «out-in», les noyaux à faible fuite ont des assemblages de combustible frais dans la deuxième rangée, pas à la périphérie du cœur. La périphérie contient du carburant avec une consommation de carburant plus élevée et une puissance relative inférieure et sert de bouclier de rayonnement très sophistiqué.
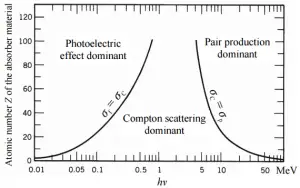
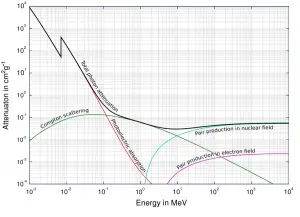
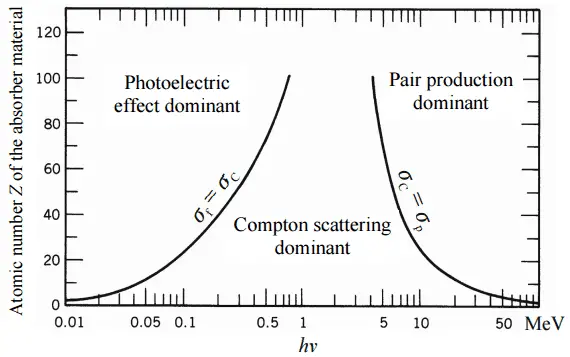
Dans les centrales nucléaires, le problème central est de se protéger contre les rayons gamma et les neutrons , car les gammes de particules chargées (telles que les particules bêta et les particules alpha) dans la matière sont très courtes. D’autre part, nous devons traiter du blindage de tous les types de rayonnements, car chaque réacteur nucléaire est une source importante de tous les types de rayonnements ionisants.
Calcul du débit de dose blindé chez les Sieverts à partir d’une surface contaminée
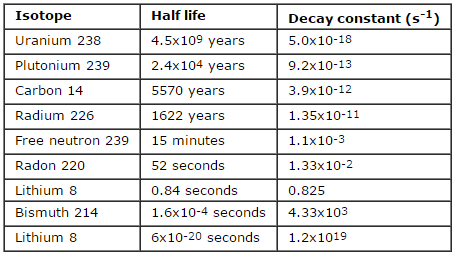
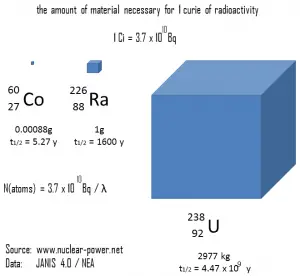
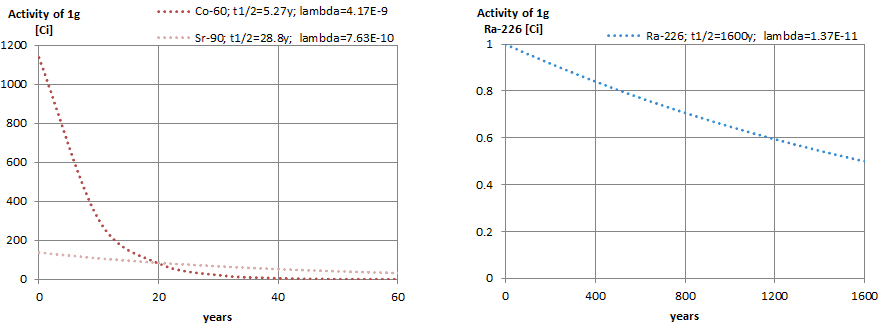
Supposons une surface contaminée par 1,0 Ci de 137 Cs . Supposons que ce contaminant puisse être aproximé par la source isotrope ponctuelle qui contient 1,0 Ci de 137 Cs , qui a une demi-vie de 30,2 ans . Notez que la relation entre la demi-vie et la quantité de radionucléide nécessaire pour donner une activité d’ un curie est indiquée ci-dessous. Cette quantité de matière peut être calculée en utilisant λ, qui est la constante de désintégration de certains nucléides:
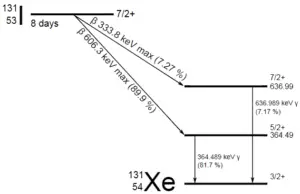
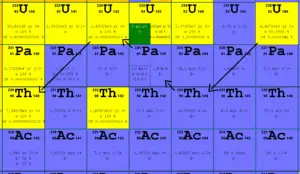
Environ 94,6 pour cent se désintègre par émission bêta vers un isomère nucléaire métastable du baryum: le baryum-137m. Le pic photonique principal de Ba-137m est de 662 keV . Pour ce calcul, supposons que toutes les désintégrations passent par ce canal.
Calculez le débit de dose de photons primaires , en sieverts par heure (Sv.h -1 ), à la surface extérieure d’un blindage en plomb de 5 cm d’épaisseur. Calculez ensuite les débits de dose équivalents et effectifs pour deux cas.
- Supposons que ce champ de rayonnement externe pénètre uniformément dans tout le corps. Cela signifie: calculer le débit de dose efficace pour tout le corps .
- Supposons que ce champ de rayonnement externe ne pénètre que dans les poumons et que les autres organes soient complètement protégés. Cela signifie: calculer le débit de dose efficace .
Notez que le débit de dose de photons primaires néglige toutes les particules secondaires. Supposons que la distance effective de la source au point de dose soit de 10 cm . Nous supposerons également que le point de dose est un tissu mou et qu’il peut raisonnablement être simulé par l’eau et nous utilisons le coefficient d’absorption d’énergie de masse pour l’eau.
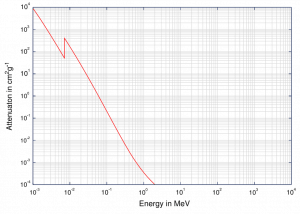
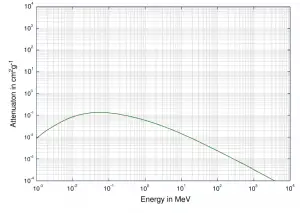
Voir aussi: Atténuation des rayons gamma
Voir aussi: Blindage des rayons gamma
Solution:
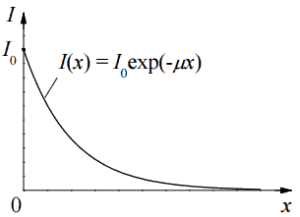
Le débit de dose des photons primaires est atténué de façon exponentielle , et le débit de dose des photons primaires, en tenant compte du blindage, est donné par:
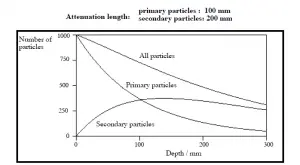
Comme on peut le voir, nous ne tenons pas compte de l’accumulation de rayonnement secondaire. Si des particules secondaires sont produites ou si le rayonnement primaire change d’énergie ou de direction, l’atténuation effective sera alors beaucoup moins importante. Cette hypothèse sous-estime généralement le véritable débit de dose, en particulier pour les écrans épais et lorsque le point de dose est proche de la surface de l’écran, mais cette hypothèse simplifie tous les calculs. Dans ce cas, le véritable débit de dose (avec l’accumulation de rayonnement secondaire) sera plus de deux fois plus élevé.
Pour calculer le débit de dose absorbé , nous devons utiliser dans la formule:
- k = 5,76 x 10 -7
- S = 3,7 x 10 10 s -1
- E = 0,662 MeV
- μ t / ρ = 0,0326 cm 2 / g (les valeurs sont disponibles au NIST)
- μ = 1,289 cm -1 (les valeurs sont disponibles au NIST)
- D = 5 cm
- r = 10 cm
Résultat:
Le débit de dose absorbé résultant en gray par heure est alors:
1) Irradiation uniforme
Puisque le facteur de pondération de rayonnement pour les rayons gamma est égal à un et que nous avons supposé le champ de rayonnement uniforme (le facteur de pondération tissulaire est également égal à l’unité), nous pouvons calculer directement le débit de dose équivalent et le débit de dose efficace (E = H T ) à partir du débit de dose absorbé:
2) Irradiation partielle
Dans ce cas, nous supposons une irradiation partielle des poumons uniquement. Ainsi, nous devons utiliser le facteur de pondération tissulaire , qui est égal à w T = 0,12 . Le facteur de pondération de rayonnement pour les rayons gamma est égal à un. En conséquence, nous pouvons calculer le débit de dose efficace comme suit:
Notez que si une partie du corps (par exemple, les poumons) reçoit une dose de rayonnement, cela représente un risque pour un effet particulièrement dommageable (par exemple, le cancer du poumon). Si la même dose est administrée à un autre organe, elle représente un facteur de risque différent.
Si nous voulons tenir compte de l’accumulation de rayonnement secondaire, nous devons inclure le facteur d’accumulation. La formule étendue pour le débit de dose est alors:
Facteurs d’accumulation pour le blindage des rayons gamma
Le facteur d’accumulation est un facteur de correction qui tient compte de l’influence du rayonnement diffusé et de toutes les particules secondaires dans le milieu lors des calculs de blindage. Si nous voulons tenir compte de l’accumulation de rayonnement secondaire, nous devons inclure le facteur d’accumulation . Le facteur d’accumulation est alors un facteur multiplicatif qui rend compte de la réponse aux photons non collidés de manière à inclure la contribution des photons diffusés. Ainsi, le facteur d’accumulation peut être obtenu en tant que rapport de la dose totale à la réponse pour la dose non prise.
La formule étendue pour le calcul du débit de dose est la suivante:
La norme ANSI / ANS-6.4.3-1991 sur les coefficients d’atténuation des rayons gamma et les facteurs d’accumulation pour les matériaux d’ingénierie contient des coefficients d’atténuation des rayons gamma et des facteurs d’accumulation pour certains matériaux et éléments d’ingénierie à utiliser dans les calculs de blindage (ANSI / ANS-6.1 .1, 1991).
……………………………………………………………………………………………………………………………….
Cet article est basé sur la traduction automatique de l’article original en anglais. Pour plus d’informations, voir l’article en anglais. Pouvez vous nous aider Si vous souhaitez corriger la traduction, envoyez-la à l’adresse: [email protected] ou remplissez le formulaire de traduction en ligne. Nous apprécions votre aide, nous mettrons à jour la traduction le plus rapidement possible. Merci