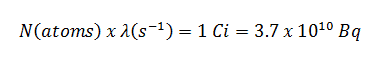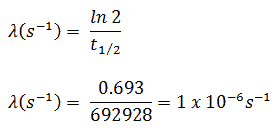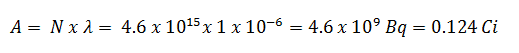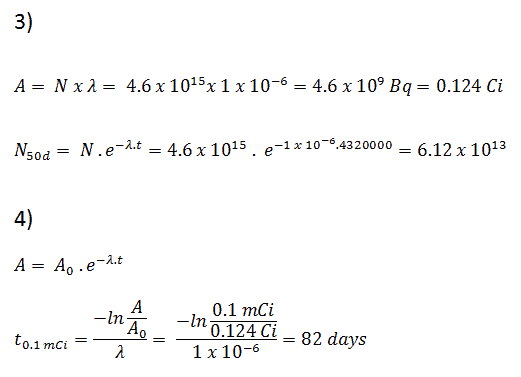L’un des termes les plus utiles pour estimer la vitesse de décomposition d’un nucléide est la demi-vie radioactive ( t 1/2 ). La demi-vie est définie comme le temps nécessaire à un isotope donné pour perdre la moitié de sa radioactivité. Comme cela a été écrit, la désintégration radioactive est un processus aléatoire au niveau d’atomes uniques, en ce sens que, selon la théorie quantique, il est impossible de prédire quand un atome particulier va se désintégrer. En d’autres termes, un noyau d’un radionucléide n’a pas de «mémoire». Un noyau ne «vieillit» pas avec le temps. Ainsi, la probabilité de sa décomposition n’augmente pas avec le temps, mais reste constante quelle que soit la durée d’existence du noyau.
Par conséquent, le taux de décroissance nucléaire peut également être mesuré en termes de demi-vies . Chaque radionucléide a sa propre demi-vie particulière qui ne change jamais, quelle que soit la quantité ou la forme du matériau (c.-à-d. Solide, liquide, gaz, élément ou composé) ou son histoire passée. Si un radio-isotope a une demi-vie de 14 jours, la moitié de ses atomes se seront désintégrés en 14 jours. Dans 14 jours de plus, la moitié de la moitié restante se décomposera, etc.
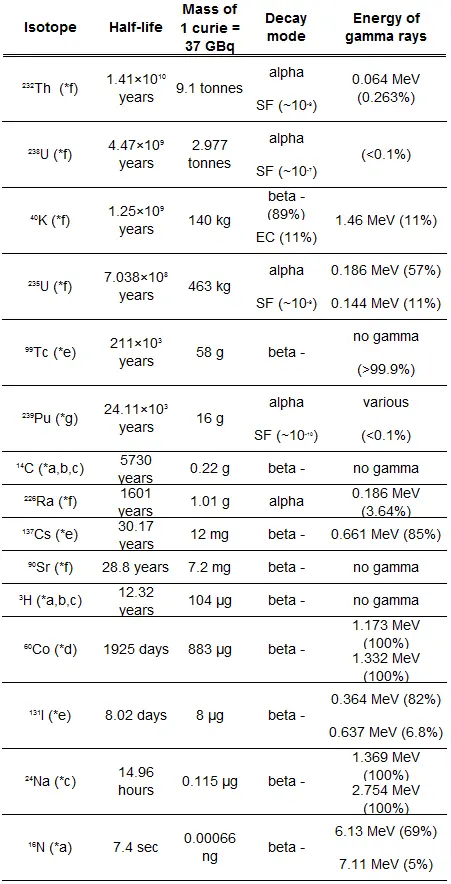
Les demi-vies varient de millionièmes de seconde pour les produits de fission hautement radioactifs à des milliards d’années pour les matériaux à vie longue (comme l’uranium naturel). Après que cinq demi-vies se soient écoulées, il ne reste que 1/32, ou 3,1%, du nombre original d’atomes. Après sept demi-vies, il ne reste que 1/128, soit 0,78%, des atomes. Le nombre d’atomes existant après 5 à 7 demi-vies peut généralement être considéré comme négligeable.
Demi-vie et radioactivité – Exemple
La relation entre la demi-vie et la quantité de radionucléide nécessaire pour donner une activité d’un curie est illustrée sur la figure. Cette quantité de matière peut être calculée en utilisant λ , qui est la constante de désintégration de certains nucléides:
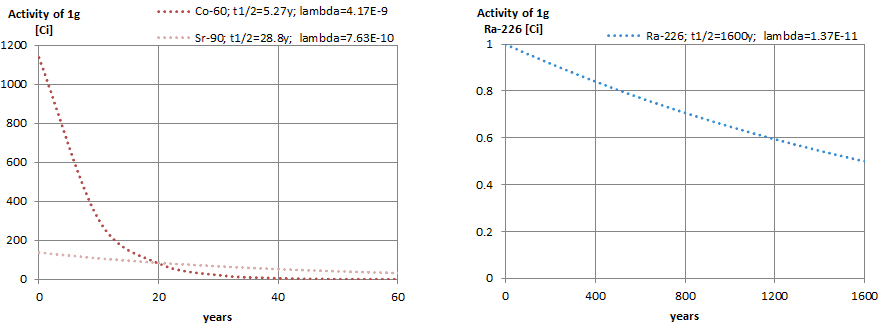
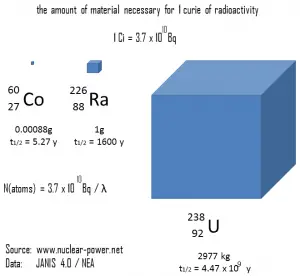La figure suivante illustre la quantité de matière nécessaire pour 1 curie de radioactivité. Il est évident que plus la demi-vie est longue, plus la quantité de radionucléide nécessaire pour produire la même activité est importante. Bien sûr, la substance à longue durée de vie restera radioactive pendant beaucoup plus longtemps. Comme on peut le voir, la quantité de matière nécessaire pour 1 curie de radioactivité peut varier d’une quantité trop petite pour être vue (0,00088 gramme de cobalt-60), à travers 1 gramme de radium-226, à près de trois tonnes d’ uranium-238 .
Exemple – Loi sur la désintégration radioactive
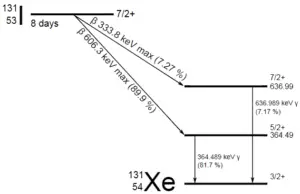Un échantillon de matériau contient 1 mikrogramme d’iode 131. Il convient de noter que l’iode 131 joue un rôle majeur en tant qu’isotope radioactif présent dans les produits de fission nucléaire et qu’il contribue de façon importante aux risques pour la santé lorsqu’il est rejeté dans l’atmosphère lors d’un accident. L’iode-131 a une demi-vie de 8,02 jours.
Calculer:
- Le nombre d’atomes d’iode-131 initialement présents.
- L’activité de l’iode 131 dans les curies.
- Le nombre d’atomes d’iode 131 qui resteront dans 50 jours.
- Temps nécessaire à l’activité pour atteindre 0,1 mCi.
Solution:
- Le nombre d’atomes d’iode-131 peut être déterminé en utilisant la masse isotopique comme ci-dessous.
N I-131 = m I-131 . N A / M I-131
N I-131 = (1 μg) x (6,02 × 10 23 noyaux / mol) / (130,91 g / mol)
N I-131 = 4,6 x 10 15 noyaux
- L’activité de l’iode 131 dans les curies peut être déterminée en utilisant sa constante de désintégration :
Dans les calculs de radioactivité, l’un des deux paramètres ( constante de désintégration ou demi-vie ), qui caractérisent le taux de décroissance, doit être connu. Il existe une relation entre la demi-vie (t 1/2 ) et la constante de désintégration λ. La relation peut être dérivée de la loi de désintégration en fixant N = ½ N o . Cela donne:
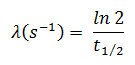où ln 2 (le logarithme naturel de 2) est égal à 0,693. Si la constante de désintégration (λ) est donnée, il est facile de calculer la demi-vie, et vice-versa.
L’iode 131 a une demi-vie de 8,02 jours (692928 s) et donc sa constante de désintégration est:
En utilisant cette valeur pour la constante de désintégration, nous pouvons déterminer l’activité de l’échantillon:
3) et 4) Le nombre d’atomes d’iode-131 qui resteront dans 50 jours (N 50d ) et le temps qu’il faudra pour que l’activité atteigne 0,1 mCi peuvent être calculés en utilisant la loi de décroissance:
Comme on peut le voir, après 50 jours, le nombre d’atomes d’iode 131 et donc l’activité sera environ 75 fois plus faible. Après 82 jours, l’activité sera environ 1200 fois plus faible. Par conséquent, le temps de dix demi-vies (facteur 2 10 = 1024) est largement utilisé pour définir l’activité résiduelle.
……………………………………………………………………………………………………………………………….
Cet article est basé sur la traduction automatique de l’article original en anglais. Pour plus d’informations, voir l’article en anglais. Pouvez vous nous aider Si vous souhaitez corriger la traduction, envoyez-la à l’adresse: [email protected] ou remplissez le formulaire de traduction en ligne. Nous apprécions votre aide, nous mettrons à jour la traduction le plus rapidement possible. Merci
