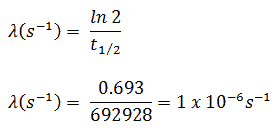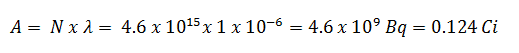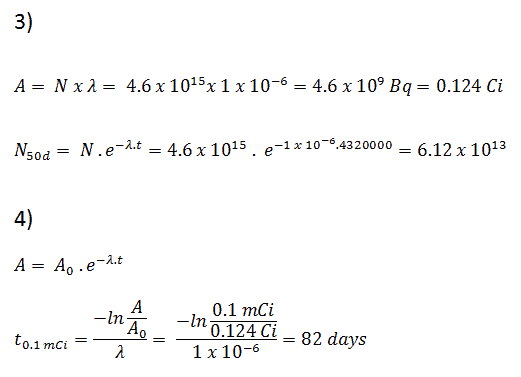Was ist Radioaktives Zerfallsgesetz – Definition

Das Zerfallsgesetz ist ein universelles Gesetz, das das statistische Verhalten einer großen Anzahl von Nukliden beschreibt.

Wie bereits geschrieben, ist der radioaktive Zerfall ein zufälliger Vorgang auf der Ebene einzelner Atome, da nach der Quantentheorie nicht vorhergesagt werden kann, wann ein bestimmtes Atom zerfallen wird. Mit anderen Worten, ein Kern eines Radionuklids hat kein „Gedächtnis“. Ein Kern „altert“ nicht im Laufe der Zeit. Somit steigt die Wahrscheinlichkeit seines Zerfalls nicht mit der Zeit, sondern bleibt konstant, egal wie lange der Kern existiert hat. Während seines unvorhersehbaren Zerfalls zersetzt sich dieser instabile Kern spontan und zufällig unter Bildung eines anderen Kerns (oder eines anderen Energiezustands – Gammazerfalls) und gibt Strahlung in Form von atomaren Teilchen oder energiereichen Strahlen ab.

Die Berechnung des Zerfalls radioaktiver Kerne ist relativ einfach, da es nur ein Grundgesetz gibt, das den gesamten Zerfallsprozess regelt.

Das radioaktive Zerfallsgesetz besagt, dass die Wahrscheinlichkeit pro Zeiteinheit, mit der ein Kern zerfällt, unabhängig von der Zeit konstant ist. Diese Konstante wird als Abklingkonstante bezeichnet und mit λ, „Lambda“ bezeichnet. Diese konstante Wahrscheinlichkeit kann zwischen verschiedenen Arten von Kernen stark variieren, was zu den vielen verschiedenen beobachteten Zerfallsraten führt. Der radioaktive Zerfall einer bestimmten Anzahl von Atomen (Masse) ist zeitlich exponentiell.

Zerfallsgesetz: N = Ne- ^λt

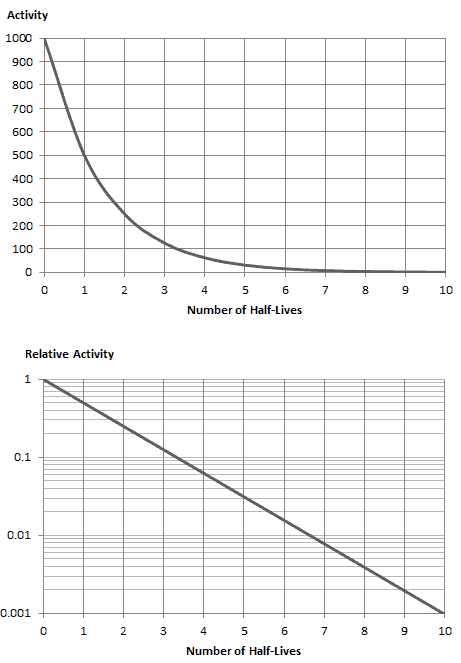
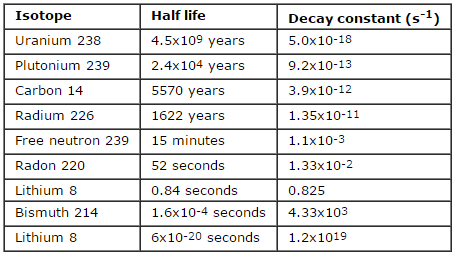
Die Rate des nuklearen Zerfalls wird auch in Form von Halbwertszeiten gemessen . Die Halbwertszeit ist die Zeit, die ein bestimmtes Isotop benötigt, um die Hälfte seiner Radioaktivität zu verlieren. Wenn ein Radioisotop eine Halbwertszeit von 14 Tagen hat, ist die Hälfte seiner Atome innerhalb von 14 Tagen zerfallen. In weiteren 14 Tagen verfällt die Hälfte der verbleibenden Hälfte und so weiter. Die Halbwertszeiten reichen von Millionstelsekunden für hochradioaktive Spaltprodukte bis zu Milliarden von Jahren für langlebige Materialien (wie natürlich vorkommendes Uran). Beachte daskurze Halbwertszeiten gehen mit großen Zerfallskonstanten einher. Radioaktives Material mit einer kurzen Halbwertszeit ist (zum Zeitpunkt der Herstellung) viel radioaktiver, verliert jedoch offensichtlich seine Radioaktivität schnell. Egal wie lang oder kurz die Halbwertszeit ist, nach Ablauf von sieben Halbwertszeiten verbleibt weniger als 1 Prozent der ursprünglichen Aktivität.

Das radioaktive Zerfallsgesetz kann auch für Aktivitätsberechnungen oder Massenberechnungen von radioaktivem Material abgeleitet werden:

(Anzahl der Kerne) N = Ne – ^λt     (Aktivität) A = Ae – ^λt      (Masse) m = me – ^λt

wobei N (Anzahl der Partikel) die Gesamtzahl der Partikel in der Probe ist, A (Gesamtaktivität) die Anzahl der Zerfälle pro Zeiteinheit einer radioaktiven Probe ist, m die Masse des verbleibenden radioaktiven Materials ist.

Aktivität – Spezifische Aktivität

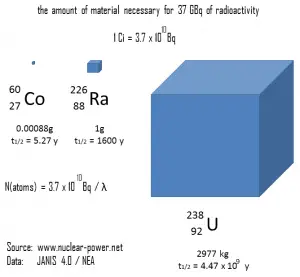Ein Maß für die Radioaktivität (Aktivität) basiert auf der Zählung der Zerfälle pro Sekunde . Die SI- Aktivitätseinheit ist das Becquerel (Bq), das einer reziproken Sekunde entspricht. Die Aktivität hängt nur von der Anzahl der Zerfälle pro Sekunde ab, nicht von der Art des Zerfalls, der Energie der Zerfallsprodukte oder den biologischen Auswirkungen der Strahlung. Es kann verwendet werden, um die Emissionsrate ionisierender Strahlung zu charakterisieren. Spezielle Aktivitätist die Aktivität pro Menge eines Radionuklids, daher ist die spezifische Aktivität definiert als die Aktivität pro Menge von Atomen eines bestimmten Radionuklids. Es wird normalerweise in Einheiten von Bq / g angegeben, aber eine andere häufig verwendete Aktivitätseinheit ist der Curie (Ci), der die Definition der spezifischen Aktivität in Ci / g ermöglicht.

Aktivitätseinheiten (Curie und Becquerel) können auch verwendet werden, um eine Gesamtmenge kontrollierter oder versehentlicher Freisetzungen radioaktiver Atome zu charakterisieren .

Aktivitätseinheiten

• Becquerel . Das Becquerel ist eine1974 definierte SI-Einheit der Radioaktivität . Es wurde zu Ehren von Henri Becquerel benannt, einem französischen Physiker, der 1896 die Radioaktivität entdeckte. Ein Becquerel (1Bq) entspricht 1 Zerfall pro Sekunde .
• Curie . Der Curie ist eine1910 definierteNicht-SI- Einheit der Radioaktivität. Sie wurde ursprünglich als äquivalent zu der Anzahl der Zerfälle definiert, die ein Gramm Radium-226 in einer Sekunde erfahren wird. Derzeit ist ein Curie definiert als 1Ci = 3,7 x 10 ¹⁰ Zerfälle pro Sekunde .
• Rutherford . Rutherford (Symbol Rd ) ist auch eine Nicht-SI-Einheit, definiert als die Aktivität einer Menge radioaktiven Materials, in der eine Million Kerne pro Sekunde zerfallen .

Zerfallskonstante und Halbwertszeit

Bei der Berechnung der Radioaktivität muss einer von zwei Parametern ( Zerfallskonstante oder Halbwertszeit ) bekannt sein, die die Zerfallsrate charakterisieren. Es gibt eine Beziehung zwischen der Halbwertszeit (t _1/2 ) und der Abklingkonstante λ. Die Beziehung kann aus dem Zerfallsgesetz abgeleitet werden, indem N = ½ N _{o gesetzt wird} . Das gibt:

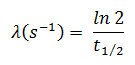wobei ln 2 (das natürliche log von 2) gleich 0,693 ist. Wenn die Abklingkonstante (λ) angegeben ist, ist es einfach, die Halbwertszeit zu berechnen und umgekehrt.

Bateman-Gleichungen

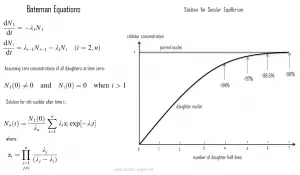In der Physik sind die Bateman-Gleichungen ein Satz von Differentialgleichungen erster Ordnung, die die zeitliche Entwicklung von Nuklidkonzentrationen beschreiben, die eine serielle oder lineare Zerfallskette durchlaufen. Das Modell wurde 1905 von Ernest Rutherford formuliert und die analytische Lösung für den Fall des radioaktiven Zerfalls in einer linearen Kette wurde 1910 von Harry Bateman bereitgestellt. Dieses Modell kann auch in nuklearen Verarmungscodes verwendet werden, um Probleme der nuklearen Transmutation und des Zerfalls zu lösen.

Beispielsweise ist ORIGEN ein Computercodesystem zur Berechnung des Aufbaus, Zerfalls und der Verarbeitung radioaktiver Materialien. ORIGEN verwendet eine Matrixexponentialmethode, um ein großes System gekoppelter, linearer gewöhnlicher Differentialgleichungen erster Ordnung (ähnlich den Bateman-Gleichungen ) mit konstanten Koeffizienten zu lösen .

Die Bateman-Gleichungen für den Fall des radioaktiven Zerfalls von n-Nuklid-Reihen in linearer Kette, die die Nuklidkonzentrationen beschreiben, sind in der Abbildung wie folgt dargestellt.

Beispiel – Zerfallsgesetz

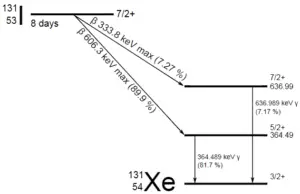Eine Materialprobe enthält 1 Mikrogramm Jod-131. Beachten Sie, dass Jod-131 eine wichtige Rolle als radioaktives Isotop in Kernspaltungsprodukten spielt und einen wesentlichen Beitrag zu den Gesundheitsrisiken leistet, wenn es während eines Unfalls in die Atmosphäre freigesetzt wird. Jod-131 hat eine Halbwertszeit von 8,02 Tagen.

Berechnung:

1. Die Anzahl der anfänglich vorhandenen Iod-131-Atome.
2. Die Aktivität des Iod-131 in Curies.
3. Die Anzahl der Iod-131-Atome, die in 50 Tagen verbleiben.
4. Die Zeit, die die Aktivität benötigt, um 0,1 mCi zu erreichen.

Lösung:

1. Die Anzahl der Atome von Iod-131 kann unter Verwendung der Isotopenmasse wie folgt bestimmt werden.

N _I-131 = m _I-131 . N _A / M _I-131

N _I-131 = (1 & mgr; g ) x (6,02 × 10 ²³ Kerne / mol) / (130,91 g / mol)

N _I-131 = 4,6 × 10 ¹⁵ Kerne

2. Die Aktivität des Iod-131 in Curies kann anhand seiner Zerfallskonstante bestimmt werden :

Das Jod-131 hat eine Halbwertszeit von 8,02 Tagen (692928 Sekunden) und daher ist seine Zerfallskonstante:

Mit diesem Wert für die Abklingkonstante können wir die Aktivität der Probe bestimmen:

3) und 4) Die Anzahl der Iod-131-Atome, die in 50 Tagen verbleiben (N _50d ), und die Zeit, die die Aktivität benötigt, um 0,1 mCi zu erreichen, können unter Verwendung des Zerfallsgesetzes berechnet werden:

Wie zu sehen ist, wird nach 50 Tagen die Anzahl der Iod-131-Atome und damit die Aktivität etwa 75-mal geringer sein. Nach 82 Tagen ist die Aktivität ungefähr 1200-mal geringer. Daher wird die Zeit von zehn Halbwertszeiten (Faktor 2 ¹⁰ = 1024) häufig verwendet, um die Restaktivität zu definieren.