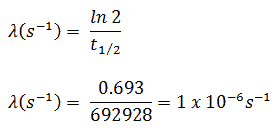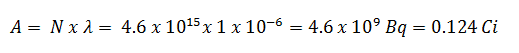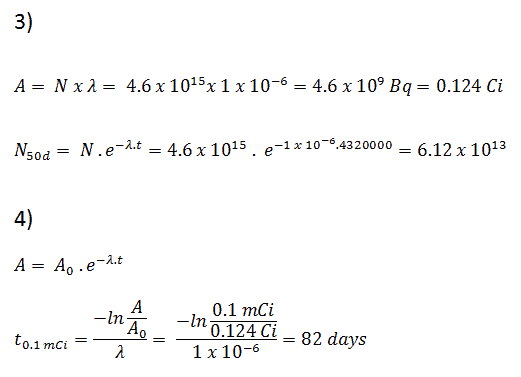O que é a Lei de Decaimento Radioativo – Definição

A lei de decaimento radioativo é uma lei universal que descreve o comportamento estatístico de um grande número de nuclídeos.

Como foi escrito, o decaimento radioativo é um processo aleatório no nível de átomos únicos, pois, segundo a teoria quântica, é impossível prever quando um determinado átomo decairá. Em outras palavras, um núcleo de um radionuclídeo não tem “memória”. Um núcleo não “envelhece” com o passar do tempo. Assim, a probabilidade de quebra não aumenta com o tempo, mas permanece constante, não importa quanto tempo o núcleo exista. Durante sua decadência imprevisível, esse núcleo instável se decompõe espontaneamente e aleatoriamente para formar um núcleo diferente (ou um estado de energia diferente – decaimento gama), emitindo radiação na forma de partículas atômicas ou raios de alta energia.

Os cálculos do decaimento dos núcleos radioativos são relativamente diretos, devido ao fato de haver apenas uma lei fundamental que governa todo o processo de decaimento.

A lei de decaimento radioativo afirma que a probabilidade por unidade de tempo que um núcleo decairá é uma constante, independente do tempo. Essa constante é chamada constante de decaimento e é denotada por λ, “lambda”. Essa probabilidade constante pode variar muito entre os diferentes tipos de núcleos, levando a muitas taxas diferentes de decaimento observadas. O decaimento radioativo de certo número de átomos (massa) é exponencial no tempo.

Lei de decaimento radioativo: N = Ne- ^λt

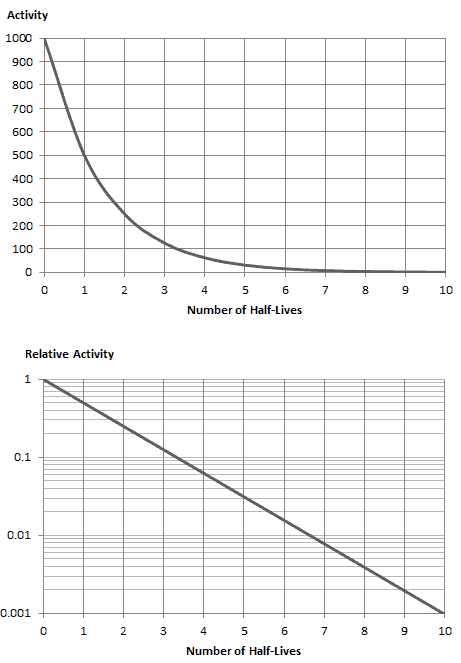
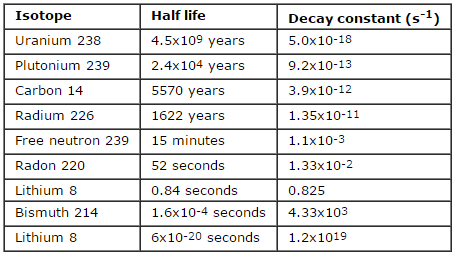
A taxa de decaimento nuclear também é medida em termos de meia-vida . A meia-vida é a quantidade de tempo que um determinado isótopo leva para perder metade de sua radioatividade. Se um radioisótopo tiver meia-vida de 14 dias, metade de seus átomos terá decaimento em 14 dias. Em mais 14 dias, metade da metade restante decairá e assim por diante. As meias-vidas variam de milionésimos de segundo para produtos de fissão altamente radioativos a bilhões de anos para materiais de longa duração (como o urânio que ocorre naturalmente). Notar quemeia-vida curta acompanha grandes constantes de decaimento. O material radioativo com meia-vida curta é muito mais radioativo (no momento da produção), mas obviamente perderá sua radioatividade rapidamente. Não importa quanto tempo a meia-vida seja curta ou curta, depois que sete meias-vidas tiverem passado, resta menos de 1% da atividade inicial.

A lei de decaimento radioativo também pode ser derivada para cálculos de atividade ou massa de cálculos de material radioativo:

(Número de núcleos) N = Ne ^-λt     (Atividade) A = Ae ^-λt      (Massa) m = me ^-λt

, onde N (número de partículas) é o número total de partículas na amostra, A (atividade total) é o número de decaimentos por unidade de tempo de uma amostra radioativa, m é a massa do material radioativo restante.

Atividade – Atividade Específica

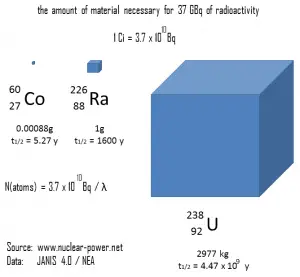Uma medida de radioatividade (atividade) é baseada na contagem de desintegrações por segundo . A unidade de atividade do SI é o becquerel (Bq), igual a um segundo recíproco. A atividade depende apenas do número de decaimentos por segundo, não do tipo de decaimento, da energia dos produtos de decaimento ou dos efeitos biológicos da radiação. Pode ser usado para caracterizar a taxa de emissão de radiação ionizante. Atividade específicaé a atividade por quantidade de um radionuclídeo, portanto, atividade específica é definida como a atividade por quantidade de átomos de um determinado radionuclídeo. Geralmente é dado em unidades de Bq / g, mas outra unidade de atividade comumente usada é a curie (Ci), permitindo a definição de atividade específica em Ci / g.

As unidades de atividade (curie e becquerel) também podem ser usadas para caracterizar uma quantidade total de liberações controladas ou acidentais de átomos radioativos .

Unidades de Atividade

• Becquerel . O becquerel é a unidade de radioatividade SI definida em 1974. É nomeado em homenagem a Henri Becquerel, físico francês que descobriu a radioatividade em 1896. Um becquerel (1Bq) é igual a 1 desintegração por segundo .
• Curie . O curie é uma unidade de radioatividade não SIdefinida em 1910. Foi originalmente definida como equivalente ao número de desintegrações pelas quais um grama de rádio-226 sofrerá em um segundo . Atualmente, um curie é definido como 1Ci = 3,7 x 10 ¹⁰ desintegrações por segundo .
• Rutherford . Rutherford (símbolo Rd ) também é uma unidade não SI definida como a atividade de uma quantidade de material radioativo na qual um milhão de núcleos decai por segundo .

Decaimento constante e meia-vida

Nos cálculos de radioatividade, um dos dois parâmetros ( constante de decaimento ou meia-vida ), que caracterizam a taxa de decaimento, deve ser conhecido. Existe uma relação entre a meia-vida (t _1/2 ) e a constante de decaimento λ. O relacionamento pode ser derivado da lei de decaimento, definindo N = ½ N _o . Isto dá:

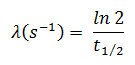onde ln 2 (o logaritmo natural de 2) é igual a 0,693. Se a constante de decaimento (λ) for dada, é fácil calcular a meia-vida e vice-versa.

Equações de Bateman

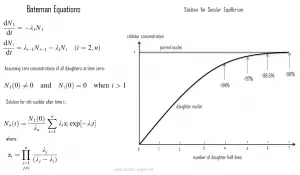Na física, as equações de Bateman são um conjunto de equações diferenciais de primeira ordem, que descrevem a evolução no tempo das concentrações de nuclídeos em cadeia de decaimento serial ou linear. O modelo foi formulado por Ernest Rutherford em 1905 e a solução analítica para o caso de decaimento radioativo em uma cadeia linear foi fornecida por Harry Bateman em 1910. Este modelo também pode ser usado em códigos de depleção nuclear para resolver problemas de transmutação e decaimento nuclear.

Por exemplo, o ORIGEN é um sistema de código de computador para calcular o acúmulo, deterioração e processamento de materiais radioativos. O ORIGEN usa um método exponencial de matriz para resolver um grande sistema de equações diferenciais ordinárias lineares de primeira ordem acopladas (semelhantes às equações de Bateman ) com coeficientes constantes.

As equações de Bateman para o caso de decaimento radioativo da série n – nuclídeo em cadeia linear que descreve as concentrações de nuclídeo são as seguintes, mostradas na figura.

Exemplo – Lei de Decaimento Radioativo

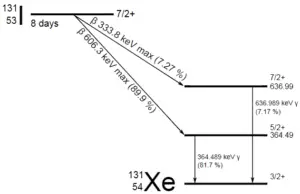Uma amostra de material contém 1 micrograma de iodo-131. Observe que o iodo-131 desempenha um papel importante como isótopo radioativo presente nos produtos de fissão nuclear e é um dos principais contribuintes para os riscos à saúde quando liberado na atmosfera durante um acidente. O iodo-131 tem uma meia-vida de 8,02 dias.

Calcular:

1. O número de átomos de iodo-131 inicialmente presentes.
2. A atividade do iodo-131 nos curies.
3. O número de átomos de iodo-131 que permanecerá em 50 dias.
4. O tempo necessário para a atividade atingir 0,1 mCi.

Solução:

1. O número de átomos de iodo-131 pode ser determinado usando a massa isotópica como abaixo.

N _-131 = m _I-131 . N _A / H _I-131

NI _-131 = (1 μg) x (6,02 × 10 ²³ núcleos / mol) / (130,91 g / mol)

NI _-131 = 4,6 x 10 ¹⁵ núcleos

2. A atividade do iodo-131 em curies pode ser determinada usando sua constante de decaimento :

O iodo-131 tem meia-vida de 8,02 dias (692928 seg) e, portanto, sua constante de decaimento é:

Usando esse valor para a constante de decaimento, podemos determinar a atividade da amostra:

3) e 4) O número de átomos de iodo-131 que permanecerá em 50 dias (N _50d ) e o tempo necessário para a atividade atingir 0,1 mCi podem ser calculados usando a lei de decaimento:

Como pode ser visto, após 50 dias o número de átomos de iodo-131 e, portanto, a atividade será cerca de 75 vezes menor. Após 82 dias, a atividade será aproximadamente 1200 vezes menor. Portanto, o tempo de dez meias-vidas (fator 2 ¹⁰ = 1024) é amplamente utilizado para definir a atividade residual.