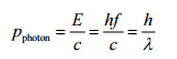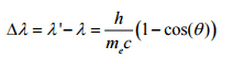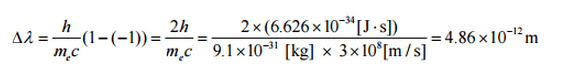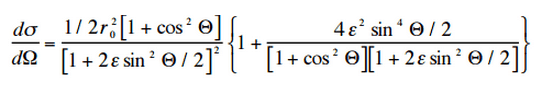Beschreibung der Gammastrahlung
Unter Gammastrahlung , auch Gammastrahlung genannt , versteht man elektromagnetische Strahlung (keine Ruhemasse, keine Ladung) mit sehr hohen Energien. Gammastrahlen sind energiereiche Photonen mit sehr kurzen Wellenlängen und damit sehr hoher Frequenz. Da es sich bei den Gammastrahlen im Wesentlichen nur um sehr energiereiche Photonen handelt, sind sie sehr durchdringende Materie und daher biologisch gefährlich. Gammastrahlen können Tausende von Fuß in der Luft wandern und leicht durch den menschlichen Körper gelangen. Gammastrahlen werden von instabilen Kernen beim Übergang von einem Zustand hoher Energie in einen Zustand niedrigerer Energieemittiert,der als Gammazerfall bekannt ist. In den meisten praktischen Laborquellen entstehen die angeregten Kernzustände beim Zerfall eines Elternradionuklids, daher typischerweise ein Gamma-Zerfallbegleitet andere Formen des Zerfalls , wie Alpha-oder Beta-Zerfall. Strahlung und auch Gammastrahlen sind überall um uns herum. In, um und über der Welt, in der wir leben. Es ist ein Teil unserer natürlichen Welt, die seit der Geburt unseres Planeten hier ist. Natürliche Quellen von Gammastrahlen auf der Erde sind unter anderem Gammastrahlen von natürlich vorkommenden Radionukliden, insbesondere Kalium-40. Kalium-40 ist ein radioaktives Isotop des Kaliums mit einer sehr langen Halbwertszeit von 1,251 × 10 9 Jahren (vergleichbar mit dem Alter der Erde). Dieses Isotop kommt im Boden, Wasser auch in Fleisch und Bananen vor. Dies ist nicht das einzige Beispiel für eine natürliche Quelle von Gammastrahlen.
Siehe auch: Entdeckung von Gammastrahlen
Eigenschaften von Gammastrahlen / Strahlung
Die Hauptmerkmale von Gammastrahlen sind in folgenden Punkten zusammengefasst:
- Gammastrahlen sind hochenergetische Photonen (etwa 10 000-mal so viel Energie wie die sichtbaren Photonen), die gleichen Photonen wie die Photonen, die den sichtbaren Bereich des elektromagnetischen Spektrums bilden – Licht.
- Photonen (Gammastrahlen und Röntgenstrahlen) können Atome durch den photoelektrischen Effekt und den Compton-Effekt direkt (obwohl sie elektrisch neutral sind) ionisieren, aber die sekundäre (indirekte) Ionisation ist viel bedeutender.
- Gammastrahlen ionisieren Materie hauptsächlich durch indirekte Ionisation .
- Obwohl eine große Anzahl möglicher Wechselwirkungen bekannt ist, gibt es drei wichtige Wechselwirkungsmechanismen mit Materie.
- Gammastrahlen bewegen sich mit Lichtgeschwindigkeit und können Tausende von Metern in der Luft zurücklegen, bevor sie ihre Energie verbrauchen.
- Da die Gammastrahlung sehr durchdringende Materie ist, muss sie durch sehr dichte Materialien wie Blei oder Uran abgeschirmt werden.
- Die Unterscheidung zwischen Röntgen- und Gammastrahlen ist nicht so einfach und hat sich in den letzten Jahrzehnten geändert. Nach der derzeit gültigen Definition werden Röntgenstrahlen von Elektronen außerhalb des Kerns emittiert , während Gammastrahlen vom Kern emittiert werden .
- Gammastrahlen begleiten häufig die Emission von Alpha- und Betastrahlung .

Quelle: Wikimedia Commons
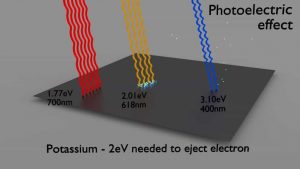
Photoelektrischer Effekt
- Der photoelektrische Effekt dominiert bei niedrigen Energien von Gammastrahlen .
- Der photoelektrische Effekt führt zur Emission von Photoelektronen aus Materie, wenn Licht ( Photonen ) auf sie scheint.
- Die maximale Energie, die ein Elektron in einer Wechselwirkung empfangen kann, ist hν .
- Elektronen werden durch den photoelektrischen Effekt nur dann emittiert, wenn das Photon eine Schwellenenergie erreicht oder überschreitet .
- Ein freies Elektron (z. B. aus einer Atomwolke) kann nicht die gesamte Energie des einfallenden Photons absorbieren. Dies ist ein Ergebnis der Notwendigkeit, sowohl Impuls als auch Energie zu sparen.
- Der Querschnitt für die Emission von n = 1 (K-Schale) Photoelektronen ist höher als der von n = 2 (L-Schale) Photoelektronen. Dies ist ein Ergebnis der Notwendigkeit, Schwung und Energie zu sparen.
Siehe auch: Albert Einstein und der photoelektrische Effekt
Definition des photoelektrischen Effekts
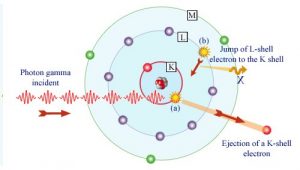
Beim photoelektrischen Effekt unterliegt ein Photon einer Wechselwirkung mit einem Elektron, das in einem Atom gebunden ist. Bei dieser Wechselwirkung verschwindet das einfallende Photon vollständig und ein energetisches Photoelektron wird vom Atom aus einer seiner gebundenen Schalen ausgestoßen . Die kinetische Energie des ausgestoßenen Photoelektron (E e ) ist gleich der einfallenden Photonenenergie (hν) abzüglich der Bindungsenergie des Photoelektron in seiner ursprünglichen Hülle (E b ).
E e = hν-E b
Daher werden Photoelektronen nur dann durch den photoelektrischen Effekt emittiert, wenn das Photon eine Schwellenenergie – die Bindungsenergie des Elektrons – die Austrittsarbeit des Materials erreicht oder überschreitet . Bei Gammastrahlen mit Energien von mehr als Hunderten keV trägt das Photoelektron den größten Teil der einfallenden Photonenenergie ab – hν.
Nach einer photoelektrischen Wechselwirkung entsteht ein ionisiertes Absorberatom mit einer Lücke in einer seiner gebundenen Schalen . Diese Lücke wird schnell durch ein Elektron aus einer Hülle mit geringerer Bindungsenergie (andere Schalen) oder durch Einfangen eines freien Elektrons aus dem Material gefüllt. Die Umlagerung von Elektronen aus anderen Schalen schafft eine weitere Lücke, die wiederum von einem Elektron aus einer noch niedrigeren Bindungsenergieschale gefüllt wird. Daher kann auch eine Kaskade charakteristischerer Röntgenstrahlen erzeugt werden. Die Wahrscheinlichkeit einer charakteristischen Röntgenemission nimmt mit abnehmender Ordnungszahl des Absorbers ab. Manchmal tritt die Emission eines Auger-Elektrons auf.
Quelle: laradioactivite.com/
Querschnitte des photoelektrischen Effekts
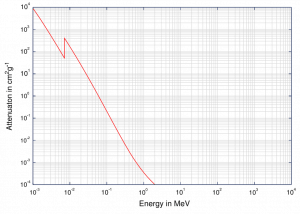
Bei kleinen Werten der Gammastrahlenenergie dominiert der photoelektrische Effekt . Der Mechanismus wird auch für Materialien mit hoher Ordnungszahl Z verbessert. Es ist nicht einfach, einen analytischen Ausdruck für die Wahrscheinlichkeit der photoelektrischen Absorption von Gammastrahlen pro Atom über alle Bereiche von Gammastrahlenenergien abzuleiten. Die Wahrscheinlichkeit der photoelektrischen Absorption pro Masseneinheit ist ungefähr proportional zu:
τ (photoelektrisch) = Konstante x Z N / E 3.5
wobei Z die Ordnungszahl ist, variiert der Exponent n zwischen 4 und 5. E ist die Energie des einfallenden Photons. Die Proportionalität zu höheren Potenzen der Ordnungszahl Z ist der Hauptgrund für die Verwendung von Materialien mit hohem Z wie Blei oder abgereichertem Uran in Gammastrahlenschilden.
Obwohl die Wahrscheinlichkeit der photoelektrischen Absorption von Gammaphotonen im Allgemeinen mit zunehmender Photonenenergie abnimmt, gibt es scharfe Diskontinuitäten in der Querschnittskurve. Diese werden als „Absoptionskanten“ bezeichnet.und sie entsprechen den Bindungsenergien von Elektronen aus den gebundenen Schalen des Atoms. Für Photonen mit einer Energie knapp über dem Rand reicht die Photonenenergie gerade aus, um die photoelektrische Wechselwirkung mit Elektronen aus der gebundenen Schale, beispielsweise der K-Schale, einzugehen. Die Wahrscheinlichkeit einer solchen Wechselwirkung ist knapp über dieser Kante viel größer als die von Energiephotonen etwas unterhalb dieser Kante. Für Gammaphotonen unterhalb dieser Kante ist die Wechselwirkung mit Elektronen aus der K-Schale energetisch unmöglich und daher sinkt die Wahrscheinlichkeit abrupt. Diese Kanten treten auch bei Bindungsenergien von Elektronen aus anderen Schalen (L, M, N… ..) auf.
Compton-Effekt
Schlüsselmerkmale der Compton-Effekt
- Bei Zwischenenergien dominiert die Compton-Effekt .
- Es ist die Streuung von Photonen durch Atomelektronen
- Photonen erfahren eine Wellenlängenverschiebung, die als Compton-Verschiebung bezeichnet wird.
- Die auf das Rückstoßelektron übertragene Energie kann von Null bis zu einem großen Teil der einfallenden Gammastrahlenenergie variieren
Definition der Compton-Effekt
Compton – Streuung ist die unelastische oder nicht – klassische Streuung eines Photons (die eine Röntgen- oder Gammastrahlen kann Photon ) durch ein geladenes Teilchen, in der Regel eines Elektron. Bei der Compton-Effekt wird das einfallende Gammastrahlenphoton um einen Winkel Θ in Bezug auf seine ursprüngliche Richtung abgelenkt. Diese Ablenkung führt zu einer Abnahme der Energie (Abnahme der Photonenfrequenz) des Photons und wird als Compton-Effekt bezeichnet . Das Photon überträgt einen Teil seiner Energie auf das Rückstoßelektron . Die auf das Rückstoßelektron übertragene Energie kann von Null bis zu einem großen Teil der einfallenden Gammastrahlenenergie variieren, da alle Streuwinkel möglich sind. Die Compton-Effekt wurde 1923 von AHCompton beobachtetan der Washington University in St. Louis. Compton erhielt 1927 den Nobelpreis für Physik für dieses neue Verständnis der Teilchennatur von Photonen.
Compton Scattering Formula
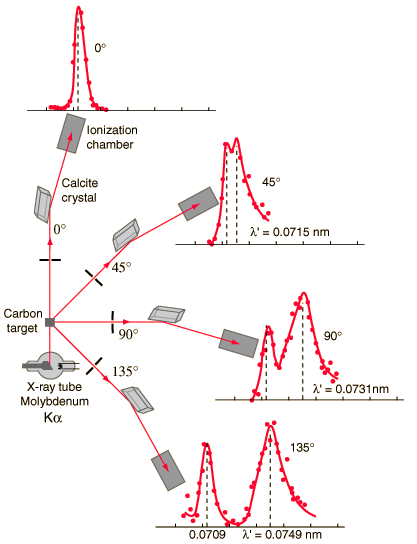
Die Compton-Formel wurde 1923 in der Physical Review veröffentlicht. Compton erklärte, dass die Röntgenverschiebung durch den partikelartigen Impuls von Photonen verursacht wird. Die Compton-Effektsformel ist die mathematische Beziehung zwischen der Verschiebung der Wellenlänge und dem Streuwinkel der Röntgenstrahlen. Bei der Compton-Effekt kollidiert das Photon der Frequenz f mit einem ruhenden Elektron. Bei einer Kollision prallt das Photon vom Elektron ab und gibt einen Teil seiner Anfangsenergie ab (gegeben durch die Plancksche Formel E = hf). Während das Elektron an Impuls gewinnt (Masse x Geschwindigkeit), kann das Photon seine Geschwindigkeit nicht senken . Aufgrund des Impulserhaltungsgesetzes muss das Photon seinen Impuls senken, der gegeben ist durch:
Die Abnahme des Photonenimpulses muss also in eine Abnahme der Frequenz (Zunahme der Wellenlänge Δλ = λ ‚- λ ) übersetzt werden. Die Verschiebung der Wellenlänge nahm mit dem Streuwinkel gemäß der Compton-Formel zu :
Quelle: hyperphysics.phy-astr.gsu.edu
wo
λ ist die anfängliche Wellenlänge des Photons
λ ‚ ist die Wellenlänge nach der Streuung,
h ist die Planck-Konstante = 6,626 × 10 –34 Js
m e ist die Elektronenruhmasse (0,511 MeV)
c ist die Lichtgeschwindigkeit
Θ ist der Streuwinkel.
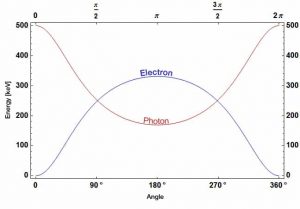
Die minimale Änderung der Wellenlänge ( λ ‚ – λ ) für das Photon tritt auf, wenn Θ = 0 ° (cos (Θ) = 1) und mindestens Null ist. Die maximale Änderung der Wellenlänge ( λ ‚ – λ ) für das Photon tritt auf, wenn Θ = 180 ° (cos (Θ) = – 1). In diesem Fall überträgt das Photon so viel Impuls wie möglich auf das Elektron. Die maximale Änderung der Wellenlänge kann aus der Compton-Formel abgeleitet werden:
Die Größe h / m e c ist als Compton-Wellenlänge des Elektrons bekannt und beträgt 2,43 × 10 –12 m .
Compton-Effekt – Querschnitte
Die Wahrscheinlichkeit der Compton-Effekt pro Wechselwirkung mit einem Atom steigt linear mit der Ordnungszahl Z an, da sie von der Anzahl der Elektronen abhängt, die für die Streuung im Zielatom verfügbar sind. Die Winkelverteilung von Photonen, die von einem einzelnen freien Elektron gestreut werden, wird durch die Klein-Nishina-Formel beschrieben :
wobei ε = E 0 / m e c 2 und r 0 der „klassische Radius des Elektrons“ ist, der ungefähr 2,8 × 10 –13 cm entspricht. Die Formel gibt die Wahrscheinlichkeit der Streuung eines Photons in das Raumwinkelelement dΩ = 2π sin Θ dΘ an, wenn die einfallende Energie E 0 ist .
Quelle: hyperphysics.phy-astr.gsu.edu/
Quelle: wikipedia.org
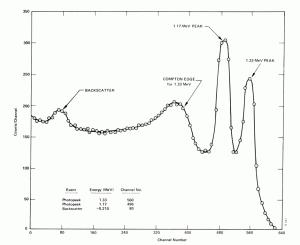
Compton Edge
Bei der Spektrophotometrie ist die Compton-Kante ein Merkmal des Spektrographen, das sich aus der Compton-Effekt im Szintillator oder Detektor ergibt. Dieses Merkmal ist auf Photonen zurückzuführen, die eine Compton-Effekt mit einem Streuwinkel von 180 ° erfahren und dann aus dem Detektor entweichen. Wenn ein Gammastrahl vom Detektor streut und entweicht, kann nur ein Bruchteil seiner Anfangsenergie in der empfindlichen Schicht des Detektors abgelagert werden. Es hängt vom Streuwinkel des Photons ab, wie viel Energie im Detektor abgeschieden wird. Dies führt zu einem Spektrum von Energien. Die Compton-Kantenenergie entspricht einem vollständig rückgestreuten Photon .
Inverse Compton-Effekt
Inverse Compton-Effekt ist die Streuung von Photonen niedriger Energie zu hohen Energien durch relativistische Elektronen. Relativistische Elektronen können die Energie von Photonen mit niedriger Energie um einen potenziell enormen Betrag steigern (sogar Gammastrahlen können erzeugt werden). Dieses Phänomen ist in der Astrophysik sehr wichtig.
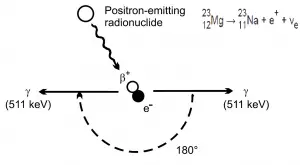
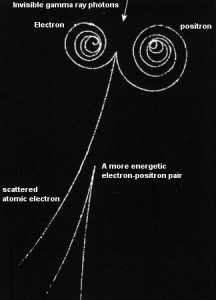
Produktion von Positronen-Elektronenpaaren
Im Allgemeinen ist die Paarproduktion ein Naturphänomen, bei dem Energie direkt in Materie umgewandelt wird . Das Phänomen der Paarproduktion kann auf zwei verschiedene Arten betrachtet werden. Ein Weg ist als Teilchen und Antiteilchen und der andere ist als Teilchen und Loch . Der erste Weg kann durch die Bildung von Elektronen und Positronen aus einem Paket elektromagnetischer Energie ( hochenergetischer Photon – Gammastrahl ) dargestellt werden, das sich durch Materie bewegt. Dies ist eine der möglichen Arten, wie Gammastrahlen mit Materie interagieren. Bei hohen Energien dominiert diese Wechselwirkung .
Damit Elektronen-Positronenpaare erzeugt werden können, muss die elektromagnetische Energie des Photons über einer Schwellenenergie liegen , die der Ruhemasse zweier Elektronen entspricht. Die Schwellenenergie (die gesamte Ruhemasse der produzierten Teilchen) für die Elektron-Positronenpaar-Produktion beträgt 1,02 MeV (2 x 0,511 MeV), da die Ruhemasse eines einzelnen Elektrons 0,511 MeV Energie entspricht.
Wenn die Energie des ursprünglichen Photons größer als 1,02 MeV ist, wird jede Energie über 1,02 MeV gemäß dem Erhaltungsgesetz zwischen der kinetischen Bewegungsenergie der beiden Teilchen aufgeteilt.
Das Vorhandensein eines elektrischen Feldes eines schweren Atoms wie Blei oder Uran ist wesentlich, um die Erhaltung von Impuls und Energie zu gewährleisten . Um sowohl die Impulserhaltung als auch die Energie zu erhalten, muss der Atomkern einen gewissen Impuls erhalten. Daher ist eine Photonenpaar – Produktion kann im freien Raum nicht auftreten .
Darüber hinaus ist das Positron das Antiteilchen des Elektrons. Wenn ein Positron zur Ruhe kommt, interagiert es mit einem anderen Elektron, was zur Vernichtung der beiden Teilchen und zur vollständigen Umwandlung ihrer Ruhemasse in reine Energie führt (gemäß die E = mc 2 -Formel) in Form von zwei entgegengesetzt gerichteten 0,511 MeV-Gammastrahlen (Photonen). Das Phänomen der Paarproduktion ist daher mit der Erzeugung und Zerstörung von Materie in einer Reaktion verbunden.
Produktion von Positronen-Elektronenpaaren – Querschnitt
Die Wahrscheinlichkeit einer Paarbildung, die durch einen Querschnitt gekennzeichnet ist, ist eine sehr komplizierte Funktion, die auf der Quantenmechanik basiert . Im Allgemeinen nimmt der Querschnitt ungefähr mit dem Quadrat der Ordnungszahl (σ p ~ Z 2 ) zu und mit der Photonenenergie zu, aber diese Abhängigkeit ist viel komplexer.
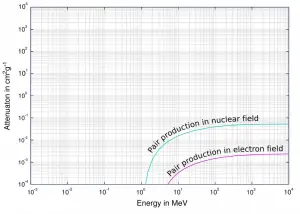 Querschnitt der Paarproduktion im Kernfeld und im Elektronenfeld.
Querschnitt der Paarproduktion im Kernfeld und im Elektronenfeld.
Dämpfung der Gammastrahlen
Der Gesamtquerschnitt der Wechselwirkung einer Gammastrahlung mit einem Atom ist gleich der Summe aller drei genannten Teilquerschnitte:
σ = σ f + σ C + σ p
- σ f – Photoelektrischer Effekt
- σ C – Compton-Effekt
- σ p – Paarproduktion
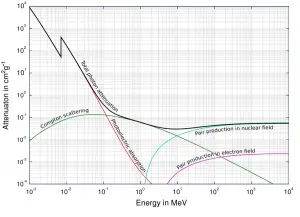
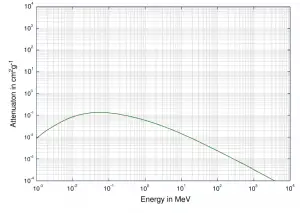
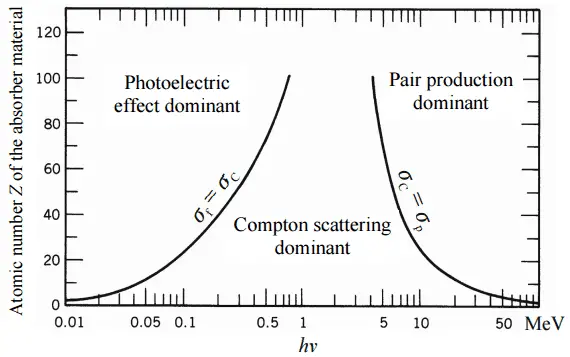
Abhängig von der Gammastrahlenenergie und dem Absorbermaterial kann einer der drei Teilquerschnitte viel größer werden als die beiden anderen. Bei kleinen Werten der Gammastrahlenenergie dominiert der photoelektrische Effekt . Bei Zwischenenergien dominiert die Compton-Effekt . Die Compton-Effekt nimmt auch mit abnehmender Ordnungszahl der Materie zu, daher ist das Dominanzintervall für Lichtkerne breiter. Schließlich dominiert die Produktion von Elektronen-Positronen-Paaren bei hohen Energien.
Basierend auf der Definition des Wechselwirkungsquerschnitts kann die Abhängigkeit der Intensität der Gammastrahlen von der Dicke des Absorbermaterials abgeleitet werden. Wenn monoenergetische Gammastrahlen zu einem schmalen Strahl kollimiert werden und der Detektor hinter dem Material nur die Gammastrahlen erfasst, die durch dieses Material hindurchgegangen sind, ohne dass eine Wechselwirkung mit diesem Material besteht, sollte die Abhängigkeit eine einfache exponentielle Abschwächung der Gammastrahlen sein . Jede dieser Wechselwirkungen entfernt das Photon entweder durch Absorption oder durch Streuung von der Detektorrichtung weg vom Strahl. Daher können die Wechselwirkungen durch eine feste Eintrittswahrscheinlichkeit pro Einheit Pfadlänge im Absorber charakterisiert werden. Die Summe dieser Wahrscheinlichkeiten heißtAbsorptionskoeffizient :
μ = τ (photoelektrisch) + σ (Compton) + κ (Paar)
Absorptionskoeffizient
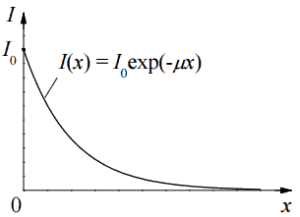
Die Dämpfung der Gammastrahlung kann dann durch die folgende Gleichung beschrieben werden.
I = I 0 .e -μx
wobei I die Intensität nach der Dämpfung ist, I o die Einfallsintensität ist, μ der lineare Dämpfungskoeffizient (cm –1 ) und die physikalische Dicke des Absorbers (cm) ist.
Die in der nebenstehenden Tabelle aufgeführten Materialien sind Luft, Wasser und verschiedene Elemente von Kohlenstoff ( Z = 6) bis Blei ( Z = 82). Ihre linearen Dämpfungskoeffizienten sind für drei Gammastrahlenenergien angegeben. Es gibt zwei Hauptmerkmale des linearen Dämpfungskoeffizienten:
- Der lineare Dämpfungskoeffizient nimmt mit zunehmender Ordnungszahl des Absorbers zu.
- Der lineare Dämpfungskoeffizient für alle Materialien nimmt mit der Energie der Gammastrahlen ab.
Halbe Wertebene
Die Halbwertsschicht drückt die Dicke des absorbierenden Materials aus, die zur Verringerung der Intensität der einfallenden Strahlung um den Faktor zwei benötigt wird . Es gibt zwei Hauptmerkmale der Halbwertsschicht:
- Die Halbwertsschicht nimmt mit zunehmender Ordnungszahl des Absorbers ab. Zum Beispiel werden 35 m Luft benötigt, um die Intensität eines 100 keV-Gammastrahls um den Faktor zwei zu reduzieren, während nur 0,12 mm Blei dasselbe bewirken können.
- Die Halbwertsschicht für alle Materialien nimmt mit der Energie der Gammastrahlen zu. Zum Beispiel von 0,26 cm für Eisen bei 100 keV bis etwa 1,06 cm bei 500 keV.
Massendämpfungskoeffizient
Bei der Charakterisierung eines absorbierenden Materials können wir manchmal den Massendämpfungskoeffizienten verwenden. Der Massendämpfungskoeffizient ist definiert als das Verhältnis des linearen Dämpfungskoeffizienten und der Absorberdichte (μ / ρ) . Die Dämpfung der Gammastrahlung kann dann durch die folgende Gleichung beschrieben werden:
I = I 0 .e – (μ / ρ) .ρl
wobei ρ die Materialdichte ist, (μ / ρ) der Massendämpfungskoeffizient ist und ρ.l die Massendicke ist. Die Maßeinheit für den Massendämpfungskoeffizienten cm 2 g -1 .
Für Zwischenenergien dominiert die Compton-Effekt und verschiedene Absorber haben ungefähr gleiche Massendämpfungskoeffizienten. Dies liegt an der Tatsache, dass der Querschnitt der Compton-Effekt proportional zum Z (Ordnungszahl) ist und daher der Koeffizient proportional zur Materialdichte ρ ist. Bei kleinen Werten der Gammastrahlenenergie oder bei hohen Werten der Gammastrahlenenergie, bei denen der Koeffizient proportional zu höheren Potenzen der Ordnungszahl Z ist (für den photoelektrischen Effekt σ f ~ Z 5 ; für die Paarproduktion σ p ~ Z 2 ), wird die Der Dämpfungskoeffizient μ ist keine Konstante.
Beispiel:
Wie viel Wasserschutz benötigen Sie, wenn Sie die Intensität eines monoenergetischen 500-keV- Gammastrahls ( schmaler Strahl ) auf 1% seiner Einfallsintensität reduzieren möchten ? Die Halbwertsschicht für 500 keV Gammastrahlen in Wasser beträgt 7,15 cm und der lineare Dämpfungskoeffizient für 500 keV Gammastrahlen in Wasser beträgt 0,097 cm -1 .
Die Frage ist recht einfach und kann durch folgende Gleichung beschrieben werden:
Wenn die Halbwertsschicht für Wasser 7,15 cm beträgt, beträgt der lineare Dämpfungskoeffizient:
Jetzt können wir die exponentielle Dämpfungsgleichung verwenden:
deshalb
Die erforderliche Wasserdicke beträgt also ca. 47,5 cm . Dies ist eine relativ große Dicke und wird durch kleine Atomzahlen von Wasserstoff und Sauerstoff verursacht. Wenn wir das gleiche Problem für Blei (Pb) berechnen , erhalten wir die Dicke x = 2,8 cm .
Lineare Dämpfungskoeffizienten
Tabelle der linearen Dämpfungskoeffizienten (in cm & supmin ; ¹ ) für verschiedene Materialien bei Gammastrahlenenergien von 100, 200 und 500 keV.
| Absorber | 100 keV | 200 keV | 500 keV |
| Luft | 0,000195 / cm | 0,000159 / cm | 0,000112 / cm |
| Wasser | 0,167 / cm | 0,136 / cm | 0,097 / cm |
| Kohlenstoff | 0,335 / cm | 0,274 / cm | 0,196 / cm |
| Aluminium | 0,435 / cm | 0,324 / cm | 0,227 / cm |
| Eisen | 2,72 / cm | 1,09 / cm | 0,655 / cm |
| Kupfer | 3,8 / cm | 1,309 / cm | 0,73 / cm |
| Führen | 59,7 / cm | 10,15 / cm | 1,64 / cm |
Halbe Wertebenen
Die Halbwertsschicht drückt die Dicke des absorbierenden Materials aus, die zur Verringerung der Intensität der einfallenden Strahlung um den Faktor zwei benötigt wird. Mit der Halbwertsschicht ist es einfach, einfache Berechnungen durchzuführen.
Quelle: www.nde-ed.org
Tabelle der Halbwertsschichten (in cm) für verschiedene Materialien bei Gammastrahlenenergien von 100, 200 und 500 keV.
| Absorber | 100 keV | 200 keV | 500 keV |
| Luft | 3555 cm | 4359 cm | 6189 cm |
| Wasser | 4,15 cm | 5,1 cm | 7,15 cm |
| Kohlenstoff | 2,07 cm | 2,53 cm | 3,54 cm |
| Aluminium | 1,59 cm | 2,14 cm | 3,05 cm |
| Eisen | 0,26 cm | 0,64 cm | 1,06 cm |
| Kupfer | 0,18 cm | 0,53 cm | 0,95 cm |
| Führen | 0,012 cm | 0,068 cm | 0,42 cm |
Gültigkeit des Exponentialgesetzes
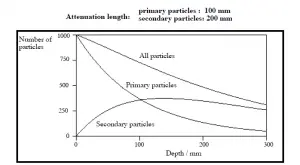
Das Exponentialgesetz beschreibt immer die Dämpfung der Primärstrahlung durch Materie. Wenn Sekundärteilchen erzeugt werden
oder wenn die Primärstrahlung ihre Energie oder Richtung ändert, ist die effektive Dämpfung viel geringer. Die Strahlung dringt tiefer in die Materie ein, als dies
allein durch das Exponentialgesetz vorhergesagt wird. Der Prozess muss bei der
Bewertung der Wirkung der Strahlenabschirmung berücksichtigt werden .
Aufbaufaktoren für die Abschirmung von Gammastrahlen
Der Aufbaufaktor ist ein Korrekturfaktor, der den Einfluss der gestreuten Strahlung plus aller Sekundärteilchen im Medium bei Abschirmungsberechnungen berücksichtigt. Wenn wir den Aufbau von Sekundärstrahlung berücksichtigen wollen, müssen wir den Aufbaufaktor einbeziehen . Der Aufbaufaktor ist dann ein multiplikativer Faktor, der die Reaktion auf die nicht kollidierten Photonen berücksichtigt, um den Beitrag der gestreuten Photonen einzuschließen. Somit kann der Aufbaufaktor als Verhältnis der Gesamtdosis zur Reaktion auf die nicht kollidierte Dosis erhalten werden.
Die erweiterte Formel für die Berechnung der Dosisleistung lautet:
Der ANSI / ANS-6.4.3-1991-Standard für Gammastrahlendämpfungskoeffizienten und Aufbaufaktoren für technische Materialien enthält abgeleitete Gammastrahlenschwächungskoeffizienten und Aufbaufaktoren für ausgewählte technische Materialien und Elemente zur Verwendung bei Abschirmungsberechnungen (ANSI / ANS-6.1) .1, 1991).
……………………………………………………………………………………………………………………………….
Dieser Artikel basiert auf der maschinellen Übersetzung des englischen Originalartikels. Weitere Informationen finden Sie im Artikel auf Englisch. Sie können uns helfen. Wenn Sie die Übersetzung korrigieren möchten, senden Sie diese bitte an: [email protected] oder füllen Sie das Online-Übersetzungsformular aus. Wir bedanken uns für Ihre Hilfe und werden die Übersetzung so schnell wie möglich aktualisieren. Danke.