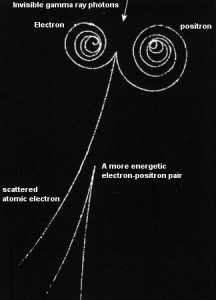
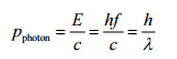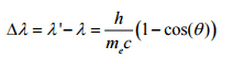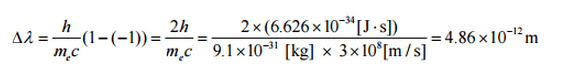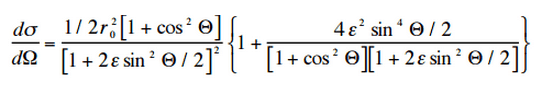Descripción de la radiación gamma
Los rayos gamma , también conocidos como radiación gamma , se refieren a la radiación electromagnética (sin masa en reposo, sin carga) de muy altas energías. Los rayos gamma son fotones de alta energíacon longitudes de onda muy cortas y, por lo tanto, de muy alta frecuencia. Dado que los rayos gamma son en sustancia solo fotones de muy alta energía, son materia muy penetrante y, por lo tanto, biológicamente peligrosos. Los rayos gamma pueden viajar miles de pies en el aire y pueden pasar fácilmente por el cuerpo humano. Los rayos gamma son emitidos por núcleos inestables en su transición de un estado de alta energía a un estado inferior conocido como desintegración gamma. En las fuentes de laboratorio más prácticas, los estados nucleares excitados se crean en la desintegración de un radionúclido original, por lo tanto, una desintegración gamma típicamenteacompaña otras formas de desintegración , como la desintegración alfa o beta. La radiación y también los rayos gamma nos rodean. En, alrededor y por encima del mundo en que vivimos. Es una parte de nuestro mundo natural que ha estado aquí desde el nacimiento de nuestro planeta. Las fuentes naturales de rayos gamma en la Tierra son, entre otros, los rayos gamma de radionucleidos naturales, particularmente el potasio-40. El potasio-40 es un isótopo radiactivo de potasio que tiene una vida media muy larga de 1.251 × 10 9 años (comparable a la edad de la Tierra). Este isótopo se puede encontrar en el suelo, el agua también en carne y plátanos. Este no es el único ejemplo de fuente natural de rayos gamma.
Ver también: descubrimiento de rayos gamma
Características de los rayos gamma / radiación
Las características clave de los rayos gamma se resumen en los siguientes puntos:
- Los rayos gamma son fotones de alta energía (aproximadamente 10 000 veces más energía que los fotones visibles), los mismos fotones que los fotones que forman el rango visible del espectro electromagnético: la luz.
- Los fotones (rayos gamma y rayos X) pueden ionizar átomos directamente (a pesar de que son eléctricamente neutros) a través del efecto fotoeléctrico y el efecto Compton, pero la ionización secundaria (indirecta) es mucho más significativa.
- Los rayos gamma ionizan la materia principalmente a través de la ionización indirecta .
- Aunque se conoce una gran cantidad de posibles interacciones, existen tres mecanismos de interacción clave con la materia.
- Los rayos gamma viajan a la velocidad de la luz y pueden viajar miles de metros en el aire antes de gastar su energía.
- Dado que la radiación gamma es una materia muy penetrante, debe estar protegida por materiales muy densos, como el plomo o el uranio.
- La distinción entre rayos X y rayos gamma no es tan simple y ha cambiado en las últimas décadas. Según la definición actualmente válida, los rayos X son emitidos por electrones fuera del núcleo, mientras que los rayos gamma son emitidos por el núcleo .
- Los rayos gamma acompañan frecuentemente la emisión de radiación alfa y beta .

Fuente: Wikimedia Commons
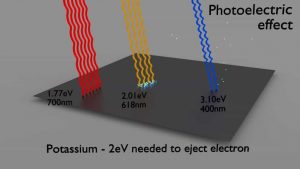
Efecto fotoeléctrico
- El efecto fotoeléctrico domina a bajas energías de rayos gamma .
- El efecto fotoeléctrico conduce a la emisión de fotoelectrones de la materia cuando la luz ( fotones ) brilla sobre ellos.
- La energía máxima que puede recibir un electrón en cualquier interacción es hν .
- Los electrones solo son emitidos por el efecto fotoeléctrico si el fotón alcanza o excede un umbral de energía .
- Un electrón libre (por ejemplo, de una nube atómica) no puede absorber toda la energía del fotón incidente. Esto es resultado de la necesidad de conservar tanto el impulso como la energía.
- La sección transversal para la emisión de n = 1 (K-shell) fotoelectrones es mayor que la de n = 2 (L-shell) fotoelectrones. Esto es el resultado de la necesidad de conservar el impulso y la energía.
Ver también: Albert Einstein y el efecto fotoeléctrico.
Definición de efecto fotoeléctrico
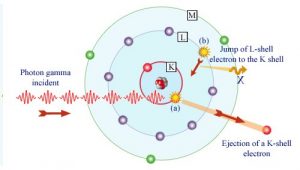
En el efecto fotoeléctrico, un fotón experimenta una interacción con un electrón que está unido a un átomo. En esta interacción, el fotón incidente desaparece por completo y el átomo expulsa un fotoelectrón energético de una de sus capas unidas . La energía cinética del fotoelectrón expulsado (E e ) es igual a la energía del fotón incidente (hν) menos la energía de unión del fotoelectrón en su capa original (E b ).
E e = hν-E b
Por lo tanto, los fotoelectrones solo son emitidos por el efecto fotoeléctrico si el fotón alcanza o excede un umbral de energía , la energía de unión del electrón, la función de trabajo del material. Para los rayos gamma con energías de más de cientos keV, el fotoelectrón se lleva la mayor parte de la energía fotónica incidente – hν.
Después de una interacción fotoeléctrica, se crea un átomo absorbente ionizado con una vacante en una de sus capas unidas . Esta vacante se llenará rápidamente con un electrón de un caparazón con una energía de unión más baja (otras capas) o mediante la captura de un electrón libre del material. La reorganización de los electrones de otras capas crea otra vacante, que, a su vez, se llena con un electrón de una capa de energía de unión aún más baja. Por lo tanto, también se puede generar una cascada de rayos X más característicos . La probabilidad de emisión de rayos X característica disminuye a medida que disminuye el número atómico del absorbedor. A veces, se produce la emisión de un electrón Auger.
Fuente: laradioactivite.com/
Secciones transversales de efecto fotoeléctrico
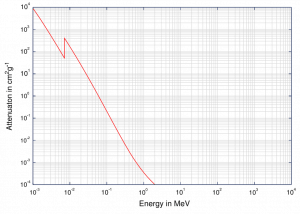
A valores pequeños de energía de rayos gamma domina el efecto fotoeléctrico . El mecanismo también se mejora para materiales de alto número atómico Z. No es simple derivar la expresión analítica para la probabilidad de absorción fotoeléctrica de rayos gamma por átomo en todos los rangos de energías de rayos gamma. La probabilidad de absorción fotoeléctrica por unidad de masa es aproximadamente proporcional a:
τ (fotoeléctrico) = constante x Z N / E 3.5
donde Z es el número atómico, el exponente n varía entre 4 y 5. E es la energía del fotón incidente. La proporcionalidad a las potencias superiores del número atómico Z es la razón principal para el uso de materiales con alto contenido de Z, como plomo o uranio empobrecido en escudos de rayos gamma.
Aunque la probabilidad de absorción fotoeléctrica del fotón gamma disminuye, en general, con el aumento de la energía del fotón, hay discontinuidades agudas en la curva de la sección transversal. Estos se llaman «bordes de absorción»y corresponden a las energías de unión de los electrones de las capas unidas a los átomos. Para los fotones con la energía justo por encima del borde, la energía del fotón es suficiente para experimentar la interacción fotoeléctrica con el electrón de la capa unida, digamos K-shell. La probabilidad de tal interacción es justo por encima de este borde, mucho mayor que la de los fotones de energía ligeramente por debajo de este borde. Para los fotones gamma por debajo de este borde, la interacción con el electrón de la capa K es energéticamente imposible y, por lo tanto, la probabilidad cae abruptamente. Estos bordes se producen también en las energías de unión de los electrones de otras capas (L, M, N … ..).
Dispersión de Compton
Características clave de la dispersión de Compton
- La dispersión de Compton domina a las energías intermedias.
- Es la dispersión de fotones por electrones atómicos.
- Los fotones experimentan un cambio de longitud de onda llamado cambio de Compton.
- La energía transferida al electrón de retroceso puede variar de cero a una gran fracción de la energía incidente de rayos gamma
Definición de dispersión de Compton
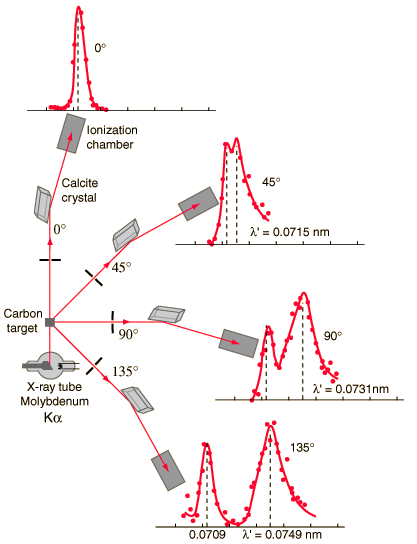
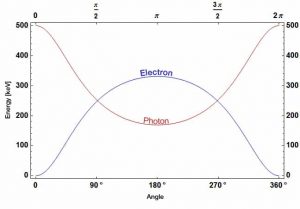
La dispersión de Compton es la dispersión inelástica o no clásica de un fotón (que puede ser un fotón de rayos X o rayos gamma ) por una partícula cargada, generalmente un electrón. En la dispersión de Compton, el fotón de rayos gamma incidente se desvía a través de un ángulo Θ con respecto a su dirección original. Esta desviación da como resultado una disminución de la energía (disminución de la frecuencia del fotón) del fotón y se denomina efecto Compton . El fotón transfiere una parte de su energía al electrón de retroceso . La energía transferida al electrón de retroceso puede variar de cero a una gran fracción de la energía de rayos gamma incidente, porque todos los ángulos de dispersión son posibles. La dispersión de Compton fue observada por AHCompton en 1923en la Universidad de Washington en St. Louis. Compton obtuvo el Premio Nobel de Física en 1927 por esta nueva comprensión sobre la naturaleza de las partículas de los fotones.
Fórmula de dispersión Compton
La fórmula de Compton se publicó en 1923 en Physical Review. Compton explicó que el cambio de rayos X es causado por el impulso de fotones en forma de partículas. La fórmula de dispersión de Compton es la relación matemática entre el cambio en la longitud de onda y el ángulo de dispersión de los rayos X. En el caso de la dispersión de Compton, el fotón de frecuencia f colisiona con un electrón en reposo. Tras la colisión, el fotón rebota en el electrón, renunciando a parte de su energía inicial (dada por la fórmula de Planck E = hf), mientras que el electrón gana impulso (masa x velocidad), el fotón no puede bajar su velocidad . Como resultado de la ley de conservación del momento, el fotón debe reducir su impulso dado por:
Por lo tanto, la disminución en el momento del fotón debe traducirse en disminución en la frecuencia (aumento en la longitud de onda Δ λ = λ ‘- λ ). El desplazamiento de la longitud de onda aumentó con el ángulo de dispersión de acuerdo con la fórmula de Compton :
λ es la longitud de onda inicial del fotóndónde
λ ‘ es la longitud de onda después de la dispersión,
h es la constante de Planck = 6.626 x 10 -34 Js
m e es la masa en reposo de electrones (0.511 MeV)
c es la velocidad de la luz
Θ es el ángulo de dispersión.
El cambio mínimo en la longitud de onda ( λ ′ – λ ) para el fotón ocurre cuando Θ = 0 ° (cos (Θ) = 1) y es al menos cero. El cambio máximo en la longitud de onda ( λ ′ – λ ) para el fotón ocurre cuando Θ = 180 ° (cos (Θ) = – 1). En este caso, el fotón transfiere al electrón la mayor cantidad de impulso posible. El cambio máximo en la longitud de onda puede derivarse de la fórmula de Compton:
La cantidad h / m e c se conoce como la longitud de onda de Compton del electrón y es igual a 2,43 × 10 −12 m .
Dispersión de Compton: secciones transversales
La probabilidad de dispersión de Compton por una interacción con un átomo aumenta linealmente con el número atómico Z, porque depende del número de electrones, que están disponibles para la dispersión en el átomo objetivo. La fórmula de Klein-Nishina describe la distribución angular de los fotones dispersados de un solo electrón libre :
donde ε = E 0 / m e c 2 y r 0 es el «radio clásico del electrón» igual a aproximadamente 2.8 x 10-13 cm. La fórmula da la probabilidad de dispersar un fotón en el elemento de ángulo sólido dΩ = 2π sen Θ dΘ cuando la energía incidente es E 0 .
Fuente: hyperphysics.phy-astr.gsu.edu/
Fuente: wikipedia.org
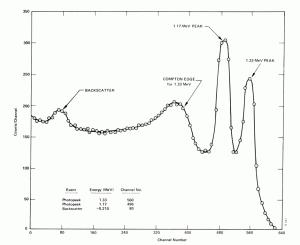
Compton Edge
En espectrofotometría, el borde de Compton es una característica del espectrógrafo que resulta de la dispersión de Compton en el centelleador o detector. Esta característica se debe a los fotones que sufren la dispersión de Compton con un ángulo de dispersión de 180 ° y luego escapan del detector. Cuando un rayo gamma se dispersa del detector y escapa, solo una fracción de su energía inicial puede depositarse en la capa sensible del detector. Depende del ángulo de dispersión del fotón, cuánta energía se depositará en el detector. Esto conduce a un espectro de energías. La energía del borde de Compton corresponde al fotón retrodispersado completo .
Dispersión inversa de Compton
La dispersión inversa de Compton es la dispersión de fotones de baja energía a altas energías por electrones relativistas. Los electrones relativistas pueden aumentar la energía de los fotones de baja energía en una cantidad potencialmente enorme (incluso se pueden producir rayos gamma). Este fenómeno es muy importante en astrofísica.
Producción de pares de positrones y electrones
En general, la producción de pares es un fenómeno de la naturaleza donde la energía se convierte directamente en materia . El fenómeno de la producción en pareja se puede ver de dos maneras diferentes. Una forma es como partícula y antipartícula y la otra es como partícula y agujero . La primera forma puede representarse mediante la formación de electrones y positrones , a partir de un paquete de energía electromagnética ( fotón de alta energía – rayos gamma ) que viaja a través de la materia. Es una de las formas posibles en que los rayos gamma interactúan con la materia. A altas energías esta interacción domina .
Para que se produzca la producción del par electrón-positrón, la energía electromagnética del fotón debe estar por encima de un umbral de energía , que es equivalente a la masa en reposo de dos electrones. La energía umbral (la masa en reposo total de las partículas producidas) para la producción de pares de electrones-positrones es igual a 1.02MeV (2 x 0.511MeV) porque la masa en reposo de un solo electrón es equivalente a 0.511MeV de energía.
Si la energía del fotón original es mayor que 1.02MeV, cualquier energía superior a 1.02MeV se divide de acuerdo con la ley de conservación dividida entre la energía cinética de movimiento de las dos partículas.
La presencia de un campo eléctrico de un átomo pesado como el plomo o el uranio es esencial para satisfacer la conservación del momento y la energía . Para satisfacer tanto la conservación del momento como la energía, el núcleo atómico debe recibir algo de impulso. Por lo tanto, no se puede producir un par de fotones en el espacio libre .
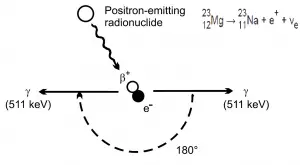
Además, el positrón es la antipartícula del electrón, por lo que cuando un positrón se detiene, interactúa con otro electrón, lo que resulta en la aniquilación de ambas partículas y la conversión completa de su masa en reposo de nuevo a energía pura (de acuerdo con la fórmula E = mc 2 ) en forma de dos rayos gamma (fotones) de 0.511 MeV opuestos. Por lo tanto, el fenómeno de producción de pares está conectado con la creación y destrucción de la materia en una reacción.
Producción de pares de positrones y electrones: sección transversal
La probabilidad de producción de pares, caracterizada por la sección transversal, es una función muy complicada basada en la mecánica cuántica . En general, la sección transversal aumenta aproximadamente con el cuadrado del número atómico (σ p ~ Z 2 ) y aumenta con la energía del fotón, pero esta dependencia es mucho más compleja.
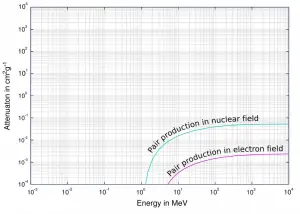 Sección transversal de la producción de pares en campo nuclear y campo de electrones.
Sección transversal de la producción de pares en campo nuclear y campo de electrones.
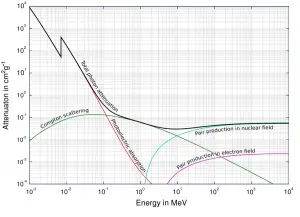
Atenuación de rayos gamma
La sección transversal total de interacción de los rayos gamma con un átomo es igual a la suma de las tres secciones transversales parciales mencionadas:
σ = σ f + σ C + σ p
- σ f – Efecto fotoeléctrico
- σ C – Dispersión de Compton
- σ p – Producción en pareja
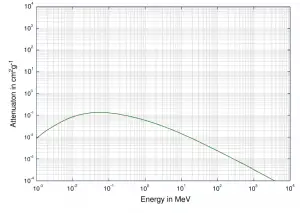
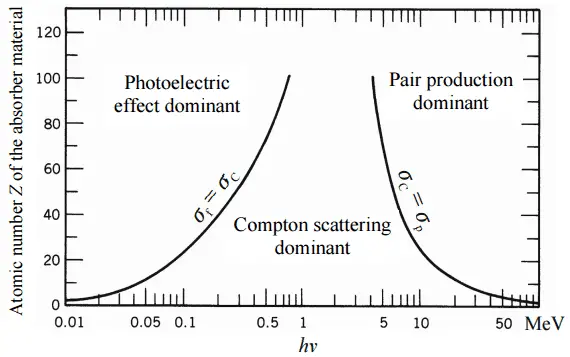
Dependiendo de la energía de los rayos gamma y del material absorbente, una de las tres secciones transversales parciales puede ser mucho más grande que las otras dos. A valores pequeños de energía de rayos gamma domina el efecto fotoeléctrico . La dispersión de Compton domina a las energías intermedias. La dispersión de compton también aumenta al disminuir el número atómico de la materia, por lo tanto, el intervalo de dominación es más amplio para los núcleos de luz. Finalmente, la producción de pares electrón-positrón domina a altas energías.
Según la definición de sección transversal de interacción, se puede deducir la dependencia de la intensidad de los rayos gamma con el grosor del material absorbente. Si los rayos gamma monoenergéticos se coliman en un haz estrecho y si el detector detrás del material solo detecta los rayos gamma que pasaron a través de ese material sin ningún tipo de interacción con este material, entonces la dependencia debería ser una simple atenuación exponencial de los rayos gamma . Cada una de estas interacciones elimina el fotón del haz por absorción o por dispersión fuera de la dirección del detector. Por lo tanto, las interacciones pueden caracterizarse por una probabilidad fija de ocurrencia por unidad de longitud de camino en el absorbedor. La suma de estas probabilidades se llamacoeficiente de atenuación lineal :
μ = τ (fotoeléctrico) + σ (Compton) + κ (par)
Coeficiente de atenuación lineal
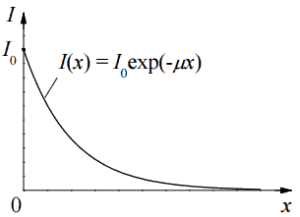
La atenuación de la radiación gamma se puede describir con la siguiente ecuación.
I = I 0 .e -μx
, donde I es la intensidad después de la atenuación, I o es la intensidad incidente, μ es el coeficiente de atenuación lineal (cm -1 ) y el espesor físico del absorbedor (cm).
Los materiales enumerados en la tabla de al lado son aire, agua y elementos diferentes desde el carbono ( Z = 6) hasta el plomo ( Z = 82) y sus coeficientes de atenuación lineal se dan para tres energías de rayos gamma. Hay dos características principales del coeficiente de atenuación lineal:
- El coeficiente de atenuación lineal aumenta a medida que aumenta el número atómico del absorbedor.
- El coeficiente de atenuación lineal para todos los materiales disminuye con la energía de los rayos gamma.
Capa de valor medio
La capa de valor medio expresa el espesor del material absorbente necesario para la reducción de la intensidad de radiación incidente en un factor de dos . Hay dos características principales de la capa de valor medio:
- La capa de valor medio disminuye a medida que aumenta el número atómico del absorbedor. Por ejemplo, se necesitan 35 m de aire para reducir la intensidad de un haz de rayos gamma de 100 keV en un factor de dos, mientras que solo 0,12 mm de plomo pueden hacer lo mismo.
- La capa de valor medio para todos los materiales aumenta con la energía de los rayos gamma. Por ejemplo, desde 0,26 cm para hierro a 100 keV hasta aproximadamente 1,06 cm a 500 keV.
Coeficiente de atenuación masiva
Al caracterizar un material absorbente, a veces podemos usar el coeficiente de atenuación de masa. El coeficiente de atenuación de masa se define como la relación del coeficiente de atenuación lineal y la densidad del absorbedor (μ / ρ) . La atenuación de la radiación gamma se puede describir con la siguiente ecuación:
I = I 0 .e – (μ / ρ) .ρl
, donde ρ es la densidad del material, (μ / ρ) es el coeficiente de atenuación de masa y ρ.l es el espesor de la masa. La unidad de medida utilizada para el coeficiente de atenuación de masa cm 2 g -1 .
Para las energías intermedias, la dispersión de Compton domina y diferentes absorbentes tienen coeficientes de atenuación de masa aproximadamente iguales. Esto se debe al hecho de que la sección transversal de la dispersión de Compton es proporcional a la Z (número atómico) y, por lo tanto, el coeficiente es proporcional a la densidad del material ρ. A valores pequeños de energía de rayos gamma o a valores altos de energía de rayos gamma, donde el coeficiente es proporcional a las potencias más altas del número atómico Z (para efecto fotoeléctrico σ f ~ Z 5 ; para producción de pares σ p ~ Z 2 ), el El coeficiente de atenuación μ no es una constante.
Ejemplo:
¿Qué cantidad de agua necesita, si desea reducir la intensidad de un haz de rayos gamma monoenergéticos ( haz estrecho ) de 500 keV al 1% de su intensidad incidente? La capa de valor medio para los rayos gamma de 500 keV en agua es de 7.15 cm y el coeficiente de atenuación lineal para los rayos gamma de 500 keV en agua es de 0.097 cm -1 .
La pregunta es bastante simple y se puede describir mediante la siguiente ecuación:
Si la capa de valor medio para el agua es 7.15 cm, el coeficiente de atenuación lineal es:
Ahora podemos usar la ecuación de atenuación exponencial:
por lo tanto
Entonces el espesor requerido de agua es de aproximadamente 47.5 cm . Este es un espesor relativamente grande y es causado por pequeños números atómicos de hidrógeno y oxígeno. Si calculamos el mismo problema para el plomo (Pb) , obtenemos el grosor x = 2.8cm .
Coeficientes de atenuación lineal
Tabla de coeficientes de atenuación lineal (en cm-1) para diferentes materiales a energías de rayos gamma de 100, 200 y 500 keV.
| Amortiguador | 100 keV | 200 keV | 500 keV |
| Aire | 0.000195 / cm | 0.000159 / cm | 0.000112 / cm |
| Agua | 0,167 / cm | 0.136 / cm | 0,097 / cm |
| Carbón | 0.335 / cm | 0.274 / cm | 0,196 / cm |
| Aluminio | 0.435 / cm | 0.324 / cm | 0.227 / cm |
| Planchar | 2,72 / cm | 1.09 / cm | 0.655 / cm |
| Cobre | 3.8 / cm | 1.309 / cm | 0,73 / cm |
| Dirigir | 59,7 / cm | 10.15 / cm | 1,64 / cm |
Capas de valor medio
La capa de valor medio expresa el grosor del material absorbente necesario para la reducción de la intensidad de radiación incidente en un factor de dos. Con la capa de valor medio es fácil realizar cálculos simples.
Fuente: www.nde-ed.org
Tabla de capas de valor medio (en cm) para diferentes materiales con energías de rayos gamma de 100, 200 y 500 keV.
| Amortiguador | 100 keV | 200 keV | 500 keV |
| Aire | 3555 cm | 4359 cm | 6189 cm |
| Agua | 4,15 cm | 5,1 cm | 7,15 cm |
| Carbón | 2,07 cm | 2,53 cm | 3,54 cm |
| Aluminio | 1,59 cm | 2,14 cm | 3,05 cm |
| Planchar | 0,26 cm | 0,64 cm | 1,06 cm |
| Cobre | 0,18 cm | 0,53 cm | 0,95 cm |
| Dirigir | 0,012 cm | 0,068 cm | 0,42 cm |
Validez de la Ley Exponencial
La ley exponencial siempre describirá la atenuación de la radiación primaria por la materia. Si se producen partículas secundarias
o si la radiación primaria cambia su energía o dirección, entonces la atenuación efectiva será mucho menor. La radiación penetrará más profundamente en la materia de lo que
predice la ley exponencial sola. El proceso debe tenerse en cuenta al
evaluar el efecto del blindaje contra la radiación.
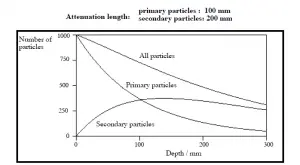
Factores de acumulación de blindaje contra rayos gamma
El factor de acumulación es un factor de corrección que considera la influencia de la radiación dispersa más cualquier partícula secundaria en el medio durante los cálculos de protección. Si queremos dar cuenta de la acumulación de radiación secundaria, entonces tenemos que incluir el factor de acumulación . El factor de acumulación es entonces un factor multiplicativo que da cuenta de la respuesta a los fotones no colidados para incluir la contribución de los fotones dispersos. Por lo tanto, el factor de acumulación se puede obtener como una relación de la dosis total a la respuesta para la dosis no contaminada.
La fórmula extendida para el cálculo de la tasa de dosis es:
El ANSI / ANS-6.4.3-1991 Coeficientes de atenuación de rayos gamma y factores de acumulación para el estándar de materiales de ingeniería, contiene coeficientes de atenuación de rayos gamma derivados y factores de acumulación para materiales y elementos de ingeniería seleccionados para usar en cálculos de blindaje (ANSI / ANS-6.1 .1, 1991).
……………………………………………………………………………………………………………………………….
Este artículo se basa en la traducción automática del artículo original en inglés. Para más información vea el artículo en inglés. Puedes ayudarnos. Si desea corregir la traducción, envíela a: [email protected] o complete el formulario de traducción en línea. Agradecemos su ayuda, actualizaremos la traducción lo antes posible. Gracias.