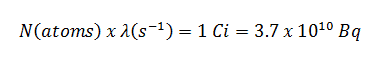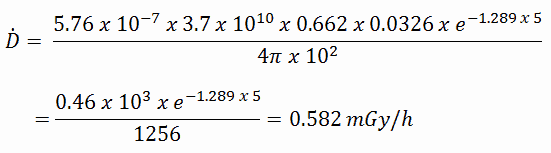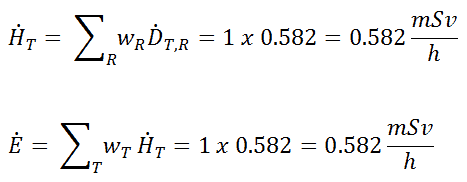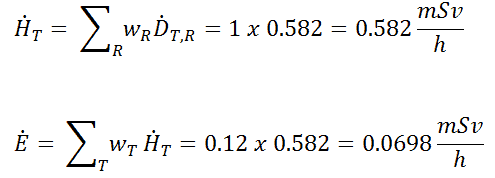Qu’est-ce qu’une dose efficace – Calcul – Exemple – Définition

En radioprotection, la dose efficace est une quantité de dose définie comme la somme des doses équivalentes aux tissus pondérées par les facteurs de pondération des organes (tissus) de la CIPR , w _T , qui prend en compte la sensibilité variable des différents organes et tissus aux rayonnements . La dose efficace est donnée le symbole E . L’unité SI de E est le sievert (Sv) ou mais rem (roentgen équivalent man) est encore couramment utilisé ( 1 Sv = 100 rem ). L’unité de sievert a été nommée d’après le scientifique suédois Rolf Sievert, qui a effectué une grande partie des premiers travaux sur la dosimétrie en radiothérapie.

Dose efficace – Calcul du débit de dose blindé

Supposons la source isotrope ponctuelle qui contient 1,0 Ci de ¹³⁷ Cs , qui a une demi-vie de 30,2 ans . Notez que la relation entre la demi-vie et la quantité de radionucléide nécessaire pour donner une activité d’ un curie est indiquée ci-dessous. Cette quantité de matière peut être calculée en utilisant λ, qui est la constante de désintégration de certains nucléides:

Environ 94,6 pour cent se désintègre par émission bêta vers un isomère nucléaire métastable du baryum: le baryum-137m. Le pic photonique principal de Ba-137m est de 662 keV . Pour ce calcul, supposons que toutes les désintégrations passent par ce canal.

Calculez le débit de dose de photons primaires , en sieverts par heure (Sv.h ^-1 ), à la surface extérieure d’un blindage en plomb de 5 cm d’épaisseur. Calculez ensuite les débits de dose équivalents et effectifs pour deux cas.

1. Supposons que ce champ de rayonnement externe pénètre uniformément dans tout le corps. Cela signifie: calculer le débit de dose efficace pour tout le corps .
2. Supposons que ce champ de rayonnement externe ne pénètre que dans les poumons et que les autres organes soient complètement protégés. Cela signifie: calculer le débit de dose efficace .

Notez que le débit de dose de photons primaires néglige toutes les particules secondaires. Supposons que la distance effective de la source au point de dose soit de 10 cm . Nous supposerons également que le point de dose est un tissu mou et qu’il peut raisonnablement être simulé par l’eau et nous utilisons le coefficient d’absorption d’énergie de masse pour l’eau.

Voir aussi: Atténuation des rayons gamma

Voir aussi: Blindage des rayons gamma

Solution:

Le débit de dose des photons primaires est atténué de façon exponentielle , et le débit de dose des photons primaires, en tenant compte du blindage, est donné par:

Comme on peut le voir, nous ne tenons pas compte de l’accumulation de rayonnement secondaire. Si des particules secondaires sont produites ou si le rayonnement primaire change d’énergie ou de direction, l’atténuation effective sera alors beaucoup moins importante. Cette hypothèse sous-estime généralement le véritable débit de dose, en particulier pour les écrans épais et lorsque le point de dose est proche de la surface de l’écran, mais cette hypothèse simplifie tous les calculs. Dans ce cas, le véritable débit de dose (avec l’accumulation de rayonnement secondaire) sera plus de deux fois plus élevé.

Pour calculer le débit de dose absorbé , nous devons utiliser dans la formule:

• k = 5,76 x 10 ^-7
• S = 3,7 x 10 ¹⁰ s ^-1
• E = 0,662 MeV
• μ _t / ρ =  0,0326 cm ² / g (les valeurs sont disponibles au NIST)
• μ = 1,289 cm ^-1 (les valeurs sont disponibles au NIST)
• D = 5 cm
• r = 10 cm

Résultat:

Le débit de dose absorbé résultant en gray par heure est alors:

1) Irradiation uniforme

Puisque le facteur de pondération de rayonnement pour les rayons gamma est égal à un et que nous avons supposé le champ de rayonnement uniforme (le facteur de pondération tissulaire est également égal à l’unité), nous pouvons calculer directement le débit de dose équivalent et le débit de dose efficace (E = H _T ) à partir du débit de dose absorbé:

2) Irradiation partielle

Dans ce cas, nous supposons une irradiation partielle des poumons uniquement. Ainsi, nous devons utiliser le facteur de pondération tissulaire , qui est égal à w _T = 0,12 . Le facteur de pondération de rayonnement pour les rayons gamma est égal à un. En conséquence, nous pouvons calculer le débit de dose efficace comme suit:

Notez que si une partie du corps (par exemple, les poumons) reçoit une dose de rayonnement, cela représente un risque pour un effet particulièrement dommageable (par exemple, le cancer du poumon). Si la même dose est administrée à un autre organe, elle représente un facteur de risque différent.

Si nous voulons tenir compte de l’accumulation de rayonnement secondaire, nous devons inclure le facteur d’accumulation. La formule étendue pour le débit de dose est alors: