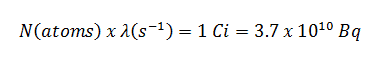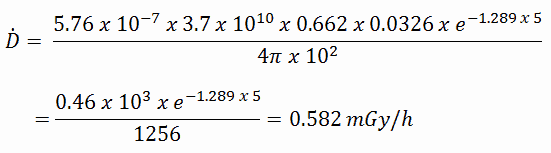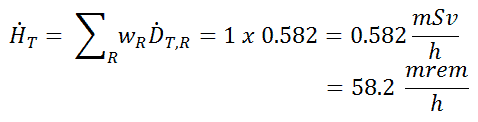 En radioprotection, le rem (une abréviation de Roentgen Equivalent Man ) est l’unité non SI de la dose équivalente , qui est principalement utilisée aux États-Unis. Le rem représente l’effet biologique équivalent du dépôt d’ une centaine d’ergs ( un rad ) d’énergie des rayons gamma dans un kilogramme de tissu humain. Le rem n’est pas dérivé de l’unité d’ exposition , le roentgen . L’acronyme est maintenant un artefact historique trompeur, car 1 roentgen dépose en fait environ 0,96 rem dans les tissus biologiques mous, lorsque tous les facteurs de pondération sont égaux à l’unité.
En radioprotection, le rem (une abréviation de Roentgen Equivalent Man ) est l’unité non SI de la dose équivalente , qui est principalement utilisée aux États-Unis. Le rem représente l’effet biologique équivalent du dépôt d’ une centaine d’ergs ( un rad ) d’énergie des rayons gamma dans un kilogramme de tissu humain. Le rem n’est pas dérivé de l’unité d’ exposition , le roentgen . L’acronyme est maintenant un artefact historique trompeur, car 1 roentgen dépose en fait environ 0,96 rem dans les tissus biologiques mous, lorsque tous les facteurs de pondération sont égaux à l’unité.
Comme cela a été écrit, le rem est utilisé pour les quantités de dose de rayonnement telles que la dose équivalente et la dose efficace . La dose équivalente (symbole H T ) est une quantité de dose calculée pour chaque organe (indice T – tissu). La dose équivalente est basée sur la dose absorbée par un organe, ajustée pour tenir compte de l’ efficacité du type de rayonnement . L’unité SI de H T est le sievert (Sv) ou mais rem (roentgen équivalent man) est encore couramment utilisé ( 1 Sv = 100 rem ).
REM et RAD
Aux fins de la radioprotection , la dose absorbée est calculée en moyenne sur un organe ou un tissu, T, et cette moyenne de dose absorbée est pondérée pour la qualité du rayonnement en termes de facteur de pondération du rayonnement , w R , pour le type et l’énergie du rayonnement incident sur le corps. Le facteur de pondération du rayonnement est un facteur sans dimension utilisé pour déterminer la dose équivalente à partir de la dose absorbée moyenne sur un tissu ou un organe et est basé sur le type de rayonnement absorbé. La dose pondérée résultante a été désignée comme la dose équivalente d’organe ou de tissu:
Une dose équivalente d’ un rem représente la quantité de dose de rayonnement qui est équivalente, en termes de dommages biologiques spécifiés , à un rad de rayons X ou de rayons gamma . Une dose d’ un rem causée par un rayonnement gamma équivaut à un dépôt d’énergie d’une centaine d’ergs d’énergie dans un kilogramme de tissu. Cela signifie qu’un rem équivaut à un rad de rayons gamma déposés dans certains tissus. D’un autre côté, des dommages biologiques similaires (un rem) ne peuvent être causés que par 1/20 rad de rayonnement alpha (dû à un w R élevé de rayonnement alpha). De même que pour les sieverts, les rems ne sont pas non plus une unité de dose physique. Par exemple, une dose absorbée de 1 rad par des particules alpha entraînera une dose équivalente de 20 rems. Cela peut sembler être un paradoxe. Cela implique que l’énergie du champ de rayonnement incident dans les ergs a augmenté d’un facteur 20, violant ainsi les lois de conservation de l’énergie . Cependant, ce n’est pas le cas. Le rem est dérivé de la quantité physique absorbée, mais prend également en compte l’ efficacité biologique du rayonnement, qui dépend du type de rayonnement et de l’énergie. Le facteur de pondération du rayonnement fait que le rem ne peut pas être une unité physique.
Un rem est également une grande quantité de dose équivalente. Une personne qui a absorbé une dose corporelle de 1 rem a absorbé cent ergs d’énergie dans chaque kg de tissu corporel (en cas de rayons gamma).
Les doses équivalentes mesurées dans l’industrie et la médecine ont souvent des doses inférieures à un rem, et les multiples suivants sont souvent utilisés:
1 mrem (millirem) = 1E-3 rem
1 krem (kilorem) = 1E3 rem
Les conversions des unités SI en d’autres unités sont les suivantes:
- 1 Sv = 100 rem
- 1 mSv = 100 mrem
Facteurs de pondération des rayonnements – ICRP
Pour le rayonnement photonique et électronique, le facteur de pondération du rayonnement a la valeur 1 indépendamment de l’énergie du rayonnement et pour le rayonnement alpha la valeur 20. Pour le rayonnement neutronique, la valeur dépend de l’énergie et s’élève à 5 à 20.

En 2007, la CIPR a publié un nouvel ensemble de facteurs de pondération des rayonnements (CIPR Publ. 103: Les recommandations de 2007 de la Commission internationale de protection radiologique). Ces facteurs sont indiqués ci-dessous.
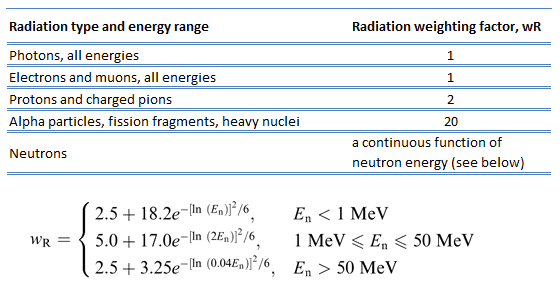
Comme le montre le tableau, aw R de 1 est pour toutes les radiations à faible LET, c’est-à-dire les rayons X et les rayons gamma de toutes les énergies ainsi que les électrons et les muons. Une courbe lisse, considérée comme une approximation, a été ajustée aux valeurs de w R en fonction de l’énergie neutronique incidente. Notez que E n est l’énergie neutronique en MeV.
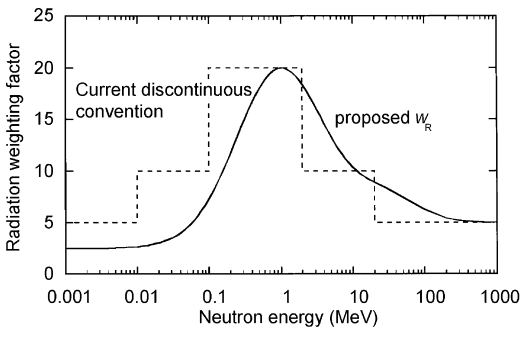
Ainsi, par exemple, une dose absorbée de 1 rad par des particules alpha conduira à une dose équivalente de 20 rem, et une dose équivalente de rayonnement est estimée avoir le même effet biologique qu’une quantité égale de dose absorbée de rayons gamma, ce qui est étant donné un facteur de pondération de 1.
Voir aussi: Facteur de qualité
Exemples de doses in rems
Nous devons noter que le rayonnement est tout autour de nous. Dans, autour et au-dessus du monde dans lequel nous vivons. C’est une force d’énergie naturelle qui nous entoure. C’est une partie de notre monde naturel qui est ici depuis la naissance de notre planète. Dans les points suivants, nous essayons d’exprimer d’énormes plages d’exposition aux rayonnements, qui peuvent être obtenues à partir de diverses sources.
- 0,005 mrem – Dormir à côté de quelqu’un
- 0,009 mrem – Vivant à moins de 30 miles d’une centrale nucléaire pendant un an
- 0,01 mrem – Manger une banane
- 0,03 mrem – Vivant à moins de 50 miles d’une centrale à charbon pendant un an
- 1 mrem – Dose journalière moyenne reçue du milieu naturel
- 2 mrem – Radiographie thoracique
- 4 mrem – Un vol en avion de 5 heures
- 60 mrem – mammographie
- 100 mrem – Limite de dose pour chaque membre du public, dose efficace totale par an
- 365 mrem – Dose annuelle moyenne reçue du milieu naturel
- 580 mrem – tomodensitométrie thoracique
- 1 000 mrem – Dose annuelle moyenne reçue du milieu naturel à Ramsar, Iran
- 2 000 mrem – tomodensitométrie unique
- 17 500 mrem – Dose annuelle de rayonnement naturel sur une plage de monazite près de Guarapari, Brésil.
- 500 000 mrem – Dose qui tue un humain avec un risque de 50% dans les 30 jours (DL50 / 30), si la dose est reçue sur une très courte durée .
Comme on peut le voir, les doses faibles sont courantes dans la vie de tous les jours. Les exemples précédents peuvent aider à illustrer les grandeurs relatives. Du point de vue des conséquences biologiques, il est très important de distinguer les doses reçues sur des périodes courtes et prolongées . Une « dose aiguë » est une dose qui se produit sur une courte période de temps, tandis qu’une « dose chronique »»Est une dose qui se prolonge pendant une période de temps prolongée afin d’être mieux décrite par un débit de dose. Des doses élevées ont tendance à tuer les cellules, tandis que de faibles doses ont tendance à les endommager ou à les modifier. De faibles doses réparties sur de longues périodes ne causent pas de problème immédiat à aucun organe du corps. Les effets de faibles doses de rayonnement se produisent au niveau de la cellule et les résultats peuvent ne pas être observés pendant de nombreuses années.
Calcul du débit de dose blindé en rems
Supposons la source isotrope ponctuelle qui contient 1,0 Ci de 137 Cs , qui a une demi-vie de 30,2 ans . Notez que la relation entre la demi-vie et la quantité de radionucléide nécessaire pour donner une activité d’ un curie est indiquée ci-dessous. Cette quantité de matière peut être calculée en utilisant λ, qui est la constante de désintégration de certains nucléides:
Environ 94,6 pour cent se désintègre par émission bêta vers un isomère nucléaire métastable du baryum: le baryum-137m. Le pic photonique principal de Ba-137m est de 662 keV . Pour ce calcul, supposons que toutes les désintégrations passent par ce canal.
Calculez le débit de dose de photons primaires , en gray par heure (Gy.h -1 ), à la surface extérieure d’un blindage en plomb de 5 cm d’épaisseur. Calculez ensuite le débit de dose équivalent en sieverts et rems. Supposons que ce champ de rayonnement externe pénètre uniformément dans tout le corps. Le débit de dose de photons primaires néglige toutes les particules secondaires. Supposons que la distance effective de la source au point de dose soit de 10 cm . Nous supposerons également que le point de dose est un tissu mou et qu’il peut raisonnablement être simulé par l’eau et nous utilisons le coefficient d’absorption d’énergie de masse pour l’eau.
Voir aussi: Atténuation des rayons gamma
Voir aussi: Blindage des rayons gamma
Solution:
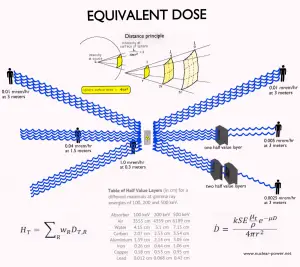
Le débit de dose des photons primaires est atténué de façon exponentielle , et le débit de dose des photons primaires, en tenant compte du blindage, est donné par:
Comme on peut le voir, nous ne tenons pas compte de l’accumulation de rayonnement secondaire. Si des particules secondaires sont produites ou si le rayonnement primaire change d’énergie ou de direction, l’atténuation effective sera alors beaucoup moins importante. Cette hypothèse sous-estime généralement le véritable débit de dose, en particulier pour les écrans épais et lorsque le point de dose est proche de la surface de l’écran, mais cette hypothèse simplifie tous les calculs. Dans ce cas, le véritable débit de dose (avec l’accumulation de rayonnement secondaire) sera plus de deux fois plus élevé.
Pour calculer le débit de dose absorbé , nous devons utiliser dans la formule:
- k = 5,76 x 10 -7
- S = 3,7 x 10 10 s -1
- E = 0,662 MeV
- μ t / ρ = 0,0326 cm 2 / g (les valeurs sont disponibles au NIST)
- μ = 1,289 cm -1 (les valeurs sont disponibles au NIST)
- D = 5 cm
- r = 10 cm
Résultat:
Le débit de dose absorbé résultant en gray par heure est alors:
Étant donné que le facteur de pondération de rayonnement pour les rayons gamma est égal à un et que nous avons supposé le champ de rayonnement uniforme, nous pouvons calculer directement le débit de dose équivalent à partir du débit de dose absorbé comme suit:
Si nous voulons tenir compte de l’accumulation de rayonnement secondaire, nous devons inclure le facteur d’accumulation. La formule étendue pour le débit de dose est alors:
……………………………………………………………………………………………………………………………….
Cet article est basé sur la traduction automatique de l’article original en anglais. Pour plus d’informations, voir l’article en anglais. Pouvez vous nous aider Si vous souhaitez corriger la traduction, envoyez-la à l’adresse: [email protected] ou remplissez le formulaire de traduction en ligne. Nous apprécions votre aide, nous mettrons à jour la traduction le plus rapidement possible. Merci