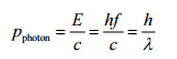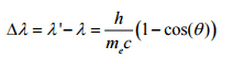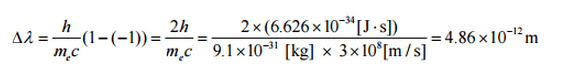Les rayons X , également connus sous le nom de rayonnement X , se réfèrent au rayonnement électromagnétique (pas de masse au repos, pas de charge) des hautes énergies. Les rayons X sont des photons de haute énergie avec des longueurs d’onde courtes et donc des fréquences très élevées. La fréquence de rayonnement est un paramètre clé de tous les photons, car elle détermine l’énergie d’un photon. Les photons sont classés en fonction des énergies des ondes radioélectriques de faible énergie et du rayonnement infrarouge, à travers la lumière visible, aux rayons X à haute énergie et aux rayons gamma .
La plupart des rayons X ont une longueur d’onde allant de 0,01 à 10 nanomètres (3 × 10 16 Hz à 3 × 10 19 Hz), correspondant à des énergies comprises entre 100 eV et 100 keV. Les longueurs d’onde des rayons X sont plus courtes que celles des rayons UV et généralement plus longues que celles des rayons gamma. La distinction entre les rayons X et les rayons gamma n’est pas si simple et a changé au cours des dernières décennies. Selon la définition actuellement valable, les rayons X sont émis par des électrons à l’extérieur du noyau, tandis que les rayons gamma sont émis par le noyau .
Étant donné que les rayons X (en particulier les rayons X durs) sont en substance des photons de haute énergie, ils constituent une matière très pénétrante et sont donc biologiquement dangereux. Les rayons X peuvent parcourir des milliers de pieds dans l’air et peuvent facilement traverser le corps humain.
Interaction des rayons X avec la matière
Bien qu’un grand nombre d’interactions possibles soient connues, il existe trois mécanismes d’interaction clés avec la matière. La force de ces interactions dépend de l’ énergie des rayons X et de la composition élémentaire du matériau, mais pas beaucoup des propriétés chimiques, car l’énergie photonique des rayons X est beaucoup plus élevée que les énergies de liaison chimique. L’absorption photoélectrique domine aux basses énergies de rayons X, tandis que la diffusion Compton domine aux énergies plus élevées.
- Absorption photoélectrique
- Diffusion de Compton
- Diffusion de Rayleigh
Absorption photoélectrique des rayons X
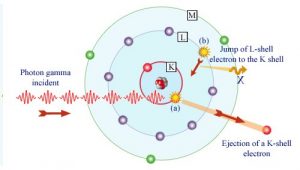
Dans l’effet photoélectrique, un photon subit une interaction avec un électron qui est lié dans un atome. Dans cette interaction, le photon incident disparaît complètement et un photoélectron énergétique est éjecté par l’atome de l’un de ses coques liées . L’énergie cinétique du photoélectron éjecté (E e ) est égale à l’énergie photonique incidente (hν) moins l’ énergie de liaison du photoélectron dans sa coque d’origine (E b ).
E e = hν-E b
Par conséquent, les photoélectrons ne sont émis par l’effet photoélectrique que si le photon atteint ou dépasse une énergie de seuil – l’énergie de liaison de l’électron – la fonction de travail du matériau. Pour les rayons X très élevés avec des énergies de plus de centaines de keV, le photoélectron emporte la majorité de l’énergie photonique incidente – hν.
Aux petites valeurs de l’énergie des rayons gamma, l’effet photoélectrique domine . Le mécanisme est également amélioré pour les matériaux de numéro atomique Z élevé. Il n’est pas simple de dériver l’expression analytique de la probabilité d’absorption photoélectrique des rayons gamma par atome sur toutes les gammes d’énergies de rayons gamma. La probabilité d’absorption photoélectrique par unité de masse est approximativement proportionnelle à:
τ (photoélectrique) = constante x Z N / E 3,5
où Z est le numéro atomique, l’exposant n varie entre 4 et 5. E est l’énergie du photon incident. La proportionnalité aux puissances supérieures du nombre atomique Z est la principale raison de l’utilisation de matériaux à forte teneur en Z, tels que le plomb ou l’uranium appauvri dans les écrans de rayons gamma.
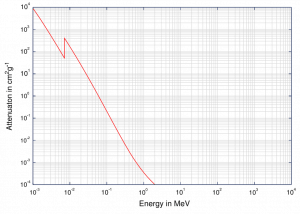 Bien que la probabilité de l’absorption photoélectrique des photons diminue, en général, avec l’augmentation de l’énergie des photons, il y a de fortes discontinuités dans la courbe de section transversale. Celles-ci sont appelées «bords d’absoption»et ils correspondent aux énergies de liaison des électrons des coquilles liées à l’atome. Pour les photons avec l’énergie juste au-dessus du bord, l’énergie des photons est juste suffisante pour subir l’interaction photoélectrique avec l’électron de la coque liée, disons K-shell. La probabilité d’une telle interaction est juste au-dessus de ce bord bien supérieure à celle des photons d’énergie légèrement en dessous de ce bord. Pour les photons en dessous de ce bord, l’interaction avec l’électron de la coquille K est énergétiquement impossible et donc la probabilité chute brusquement. Ces arêtes se produisent également aux énergies de liaison des électrons d’autres coquilles (L, M, N… ..).
Bien que la probabilité de l’absorption photoélectrique des photons diminue, en général, avec l’augmentation de l’énergie des photons, il y a de fortes discontinuités dans la courbe de section transversale. Celles-ci sont appelées «bords d’absoption»et ils correspondent aux énergies de liaison des électrons des coquilles liées à l’atome. Pour les photons avec l’énergie juste au-dessus du bord, l’énergie des photons est juste suffisante pour subir l’interaction photoélectrique avec l’électron de la coque liée, disons K-shell. La probabilité d’une telle interaction est juste au-dessus de ce bord bien supérieure à celle des photons d’énergie légèrement en dessous de ce bord. Pour les photons en dessous de ce bord, l’interaction avec l’électron de la coquille K est énergétiquement impossible et donc la probabilité chute brusquement. Ces arêtes se produisent également aux énergies de liaison des électrons d’autres coquilles (L, M, N… ..).
Diffusion Compton des rayons X
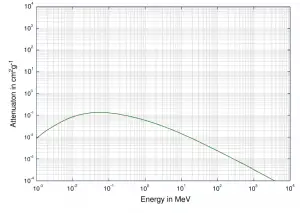 La formule Compton a été publiée en 1923 dans la Physical Review. Compton a expliqué que le déplacement des rayons X est provoqué par une impulsion de type particules de photons . La formule de diffusion Compton est la relation mathématique entre le changement de longueur d’onde et l’angle de diffusion des rayons X. Dans le cas de la diffusion Compton, le photon de fréquence f entre en collision avec un électron au repos. Lors de la collision, le photon rebondit sur l’électron, abandonnant une partie de son énergie initiale (donnée par la formule de Planck E = hf), tandis que l’électron prend de l’élan (masse x vitesse), le photon ne peut pas réduire sa vitesse. En raison de la loi de conservation de l’impulsion, le photon doit réduire son impulsion donnée par:
La formule Compton a été publiée en 1923 dans la Physical Review. Compton a expliqué que le déplacement des rayons X est provoqué par une impulsion de type particules de photons . La formule de diffusion Compton est la relation mathématique entre le changement de longueur d’onde et l’angle de diffusion des rayons X. Dans le cas de la diffusion Compton, le photon de fréquence f entre en collision avec un électron au repos. Lors de la collision, le photon rebondit sur l’électron, abandonnant une partie de son énergie initiale (donnée par la formule de Planck E = hf), tandis que l’électron prend de l’élan (masse x vitesse), le photon ne peut pas réduire sa vitesse. En raison de la loi de conservation de l’impulsion, le photon doit réduire son impulsion donnée par:
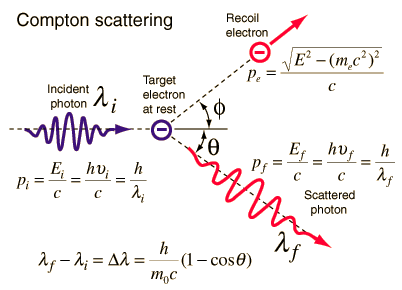
Source: hyperphysics.phy-astr.gsu.edu
La diminution de la quantité de mouvement des photons doit donc se traduire par une diminution de la fréquence (augmentation de la longueur d’onde Δ λ = λ ‘- λ ). Le décalage de la longueur d’onde augmente avec l’angle de diffusion selon la formule de Compton :
où λ est la longueur d’onde initiale du photon λ ‘ est la longueur d’onde après diffusion, h est la constante de Planck = 6,626 x 10 -34 Js, m e est la masse de repos des électrons (0,511 MeV) c est la vitesse de la lumière Θ est la diffusion angle. Le changement minimal de longueur d’onde ( λ ′ – λ ) pour le photon se produit lorsque Θ = 0 ° (cos (Θ) = 1) et est au moins nul. La variation maximale de longueur d’onde ( λ ′ – λ) pour le photon se produit lorsque Θ = 180 ° (cos (Θ) = – 1). Dans ce cas, le photon transfère à l’électron autant de mouvement que possible. Le changement maximal de longueur d’onde peut être dérivé de la formule de Compton:
La quantité h / m e c est appelée longueur d’ onde Compton de l’électron et est égale à 2,43 × 10 -12 m .
Rayleigh Scattering – Thomson Scattering
La diffusion de Rayleigh , également connue sous le nom de diffusion Thomson, est la limite de basse énergie de la diffusion Compton. L’énergie cinétique des particules et la fréquence des photons ne changent pas en raison de la diffusion. La diffusion de Rayleigh se produit à la suite d’une interaction entre un photon entrant et un électron, dont l’énergie de liaison est nettement supérieure à celle du photon entrant. Le rayonnement incident est supposé mettre l’électron en oscillation de résonance forcée de sorte que l’électron réémet un rayonnement de la même fréquence mais dans toutes les directions. Dans ce cas, le champ électrique de l’onde incidente (photon) accélère la particule chargée, ce qui, à son tour, émet un rayonnement à la même fréquence que l’onde incidente, et donc l’onde est diffusée. La diffusion de Rayleigh est significative jusqu’à ≈ 20keV et, comme la diffusion de Thomson, elle est élastique. La section efficace de diffusion totale devient une combinaison des sections efficaces de diffusion liées à Rayleigh et Compton. La diffusion de Thomson est un phénomène important en physique des plasmas et a été expliqué pour la première fois par le physicien JJ Thomson. Cette interaction a une grande importance dans le domaine de la cristallographie aux rayons X.
……………………………………………………………………………………………………………………………….
Cet article est basé sur la traduction automatique de l’article original en anglais. Pour plus d’informations, voir l’article en anglais. Pouvez vous nous aider Si vous souhaitez corriger la traduction, envoyez-la à l’adresse: [email protected] ou remplissez le formulaire de traduction en ligne. Nous apprécions votre aide, nous mettrons à jour la traduction le plus rapidement possible. Merci