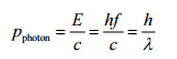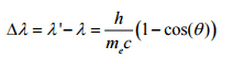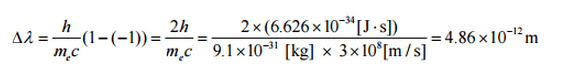Los rayos X , también conocidos como radiación X , se refieren a la radiación electromagnética (sin masa en reposo, sin carga) de altas energías. Los rayos X son fotones de alta energía con longitudes de onda cortas y, por lo tanto, de muy alta frecuencia. La frecuencia de radiación es el parámetro clave de todos los fotones, porque determina la energía de un fotón. Los fotones se clasifican según las energías de las ondas de radio de baja energía y la radiación infrarroja, a través de la luz visible, hasta los rayos X de alta energía y los rayos gamma .
La mayoría de los rayos X tienen una longitud de onda que varía de 0.01 a 10 nanómetros (3 × 10 16 Hz a 3 × 10 19 Hz), correspondiente a energías en el rango de 100 eV a 100 keV. Las longitudes de onda de los rayos X son más cortas que las de los rayos UV y típicamente más largas que las de los rayos gamma. La distinción entre rayos X y rayos gamma no es tan simple y ha cambiado en las últimas décadas. Según la definición actualmente válida, los rayos X son emitidos por electrones fuera del núcleo, mientras que los rayos gamma son emitidos por el núcleo .
Dado que los rayos X (especialmente los rayos X duros) están en una sustancia de fotones de alta energía, son materia muy penetrante y, por lo tanto, biológicamente peligrosos. Los rayos X pueden viajar miles de pies en el aire y pueden pasar fácilmente por el cuerpo humano.
Interacción de rayos X con materia
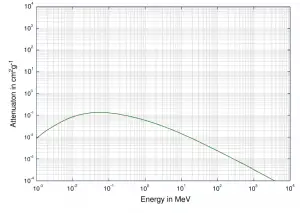
Aunque se conoce una gran cantidad de posibles interacciones, existen tres mecanismos clave de interacción con la materia. La fuerza de estas interacciones depende de la energía de los rayos X y la composición elemental del material, pero no mucho de las propiedades químicas, ya que la energía del fotón de rayos X es mucho mayor que las energías de unión química. La absorción fotoeléctrica domina a bajas energías de rayos X, mientras que la dispersión de Compton domina a energías más altas.
- Absorción fotoeléctrica
- Dispersión de Compton
- la dispersión de Rayleigh
Absorción fotoeléctrica de rayos X
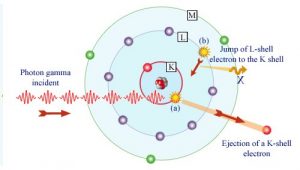
En el efecto fotoeléctrico, un fotón experimenta una interacción con un electrón que está unido a un átomo. En esta interacción, el fotón incidente desaparece por completo y el átomo expulsa un fotoelectrón energético de una de sus capas unidas . La energía cinética del fotoelectrón expulsado (E e ) es igual a la energía del fotón incidente (hν) menos la energía de unión del fotoelectrón en su capa original (E b ).
E e = hν-E b
Por lo tanto, los fotoelectrones solo son emitidos por el efecto fotoeléctrico si el fotón alcanza o excede un umbral de energía , la energía de unión del electrón, la función de trabajo del material. Para rayos X muy altos con energías de más de cientos keV, el fotoelectrón se lleva la mayor parte de la energía fotónica incidente – hν.
A valores pequeños de energía de rayos gamma domina el efecto fotoeléctrico . El mecanismo también se mejora para materiales de alto número atómico Z. No es simple derivar la expresión analítica para la probabilidad de absorción fotoeléctrica de rayos gamma por átomo en todos los rangos de energías de rayos gamma. La probabilidad de absorción fotoeléctrica por unidad de masa es aproximadamente proporcional a:
τ (fotoeléctrico) = constante x Z N / E 3.5
donde Z es el número atómico, el exponente n varía entre 4 y 5. E es la energía del fotón incidente. La proporcionalidad a las potencias superiores del número atómico Z es la razón principal para el uso de materiales con alto contenido de Z, como plomo o uranio empobrecido en escudos de rayos gamma.
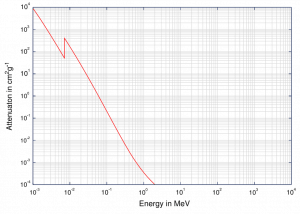 Aunque la probabilidad de la absorción fotoeléctrica del fotón disminuye, en general, con el aumento de la energía del fotón, hay discontinuidades agudas en la curva de la sección transversal. Estos se llaman «bordes de absorción»y corresponden a las energías de unión de los electrones de las capas unidas a los átomos. Para los fotones con la energía justo por encima del borde, la energía del fotón es suficiente para experimentar la interacción fotoeléctrica con el electrón de la capa unida, digamos K-shell. La probabilidad de tal interacción es justo por encima de este borde, mucho mayor que la de los fotones de energía ligeramente por debajo de este borde. Para los fotones por debajo de este borde, la interacción con el electrón de la capa K es energéticamente imposible y, por lo tanto, la probabilidad cae abruptamente. Estos bordes se producen también en las energías de unión de los electrones de otras capas (L, M, N … ..).
Aunque la probabilidad de la absorción fotoeléctrica del fotón disminuye, en general, con el aumento de la energía del fotón, hay discontinuidades agudas en la curva de la sección transversal. Estos se llaman «bordes de absorción»y corresponden a las energías de unión de los electrones de las capas unidas a los átomos. Para los fotones con la energía justo por encima del borde, la energía del fotón es suficiente para experimentar la interacción fotoeléctrica con el electrón de la capa unida, digamos K-shell. La probabilidad de tal interacción es justo por encima de este borde, mucho mayor que la de los fotones de energía ligeramente por debajo de este borde. Para los fotones por debajo de este borde, la interacción con el electrón de la capa K es energéticamente imposible y, por lo tanto, la probabilidad cae abruptamente. Estos bordes se producen también en las energías de unión de los electrones de otras capas (L, M, N … ..).
Dispersión de Compton de rayos X
 La fórmula de Compton se publicó en 1923 en Physical Review. Compton explicó que el cambio de rayos X es causado por el impulso de fotones en forma de partículas . La fórmula de dispersión de Compton es la relación matemática entre el cambio en la longitud de onda y el ángulo de dispersión de los rayos X. En el caso de la dispersión de Compton, el fotón de frecuencia f colisiona con un electrón en reposo. Tras la colisión, el fotón rebota en el electrón, renunciando a parte de su energía inicial (dada por la fórmula de Planck E = hf), mientras que el electrón gana impulso (masa x velocidad), el fotón no puede bajar su velocidad. Como resultado de la ley de conservación del momento, el fotón debe reducir su impulso dado por:
La fórmula de Compton se publicó en 1923 en Physical Review. Compton explicó que el cambio de rayos X es causado por el impulso de fotones en forma de partículas . La fórmula de dispersión de Compton es la relación matemática entre el cambio en la longitud de onda y el ángulo de dispersión de los rayos X. En el caso de la dispersión de Compton, el fotón de frecuencia f colisiona con un electrón en reposo. Tras la colisión, el fotón rebota en el electrón, renunciando a parte de su energía inicial (dada por la fórmula de Planck E = hf), mientras que el electrón gana impulso (masa x velocidad), el fotón no puede bajar su velocidad. Como resultado de la ley de conservación del momento, el fotón debe reducir su impulso dado por:
Fuente: hyperphysics.phy-astr.gsu.edu
Por lo tanto, la disminución en el momento del fotón debe traducirse en una disminución en la frecuencia (aumento en la longitud de onda Δ λ = λ ‘- λ ). El desplazamiento de la longitud de onda aumentó con el ángulo de dispersión de acuerdo con la fórmula de Compton :
donde λ es la longitud de onda inicial del fotón λ ‘ es la longitud de onda después de la dispersión, h es la constante de Planck = 6.626 x 10 -34 Js, m e es la masa de electrones en reposo (0.511 MeV) c es la velocidad de la luz Θ es la dispersión ángulo. El cambio mínimo en la longitud de onda ( λ ′ – λ ) para el fotón ocurre cuando Θ = 0 ° (cos (Θ) = 1) y es al menos cero. El cambio máximo en la longitud de onda ( λ ′ – λ) para el fotón ocurre cuando Θ = 180 ° (cos (Θ) = – 1). En este caso, el fotón transfiere al electrón la mayor cantidad de impulso posible. El cambio máximo en la longitud de onda se puede derivar de la fórmula de Compton:
La cantidad h / m e c se conoce como la longitud de onda de Compton del electrón y es igual a 2,43 × 10 −12 m .
Dispersión de Rayleigh – Dispersión de Thomson
La dispersión de Rayleigh , también conocida como dispersión de Thomson, es el límite de baja energía de la dispersión de Compton. La energía cinética de las partículas y la frecuencia de los fotones no cambian como resultado de la dispersión. La dispersión de Rayleigh ocurre como resultado de una interacción entre un fotón entrante y un electrón, cuya energía de unión es significativamente mayor que la del fotón entrante. Se supone que la radiación incidente establece el electrón en una oscilación resonante forzada de tal manera que el electrón reemite radiación de la misma frecuencia pero en todas las direcciones.. En este caso, el campo eléctrico de la onda incidente (fotón) acelera la partícula cargada, haciendo que, a su vez, emita radiación a la misma frecuencia que la onda incidente y, por lo tanto, la onda se dispersa. La dispersión de Rayleigh es significativa hasta ke 20keV y, al igual que la dispersión de Thomson, es elástica. La sección transversal de dispersión total se convierte en una combinación de las secciones transversales de dispersión ligadas de Rayleigh y Compton. La dispersión de Thomson es un fenómeno importante en la física del plasma y fue explicado por primera vez por el físico JJ Thomson. Esta interacción tiene una gran importancia en el área de la cristalografía de rayos X.
……………………………………………………………………………………………………………………………….
Este artículo se basa en la traducción automática del artículo original en inglés. Para más información vea el artículo en inglés. Puedes ayudarnos. Si desea corregir la traducción, envíela a: [email protected] o complete el formulario de traducción en línea. Agradecemos su ayuda, actualizaremos la traducción lo antes posible. Gracias.