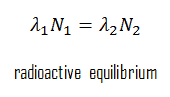En physique des désintégrations nucléaires , un équilibre radioactif existe quand un nucléide radioactif se désintègre à la même vitesse à laquelle il est produit. Le noyau se désintégrant est généralement appelé noyau parent et le noyau restant après l’événement comme noyau fille . Le noyau fille peut être stable ou radioactif. S’il est radioactif, il se désintègre en un noyau fille et ainsi de suite. Ainsi, chaque noyau parent radioactif peut initier une série de désintégrations, chaque produit de désintégration ayant sa propre constante de désintégration caractéristique.
La concentration des noyaux filles dans l’équilibre radioactif dépend principalement des proportions de demi-vies (ou constantes de désintégration ) des noyaux parents et filles. Comme le taux de production et le taux de décroissance sont égaux, le nombre d’atomes présents reste constant dans le temps. Dans tous les cas, un équilibre radioactif ne s’établit pas immédiatement, mais il n’a lieu qu’après une période de transition . Cette période est de l’ordre de quelques demi-vies du noyau le plus long de la chaîne de désintégration. Dans le cas de chaînes de désintégration radioactives, un équilibre radioactif peut être établi entre chaque membre de la chaîne de désintégration.
Comme il a été écrit, la proportionnalité des demi-vies est un paramètre clé qui détermine le type d’équilibre radioactif :
- L’équilibre radioactif n’est pas établi lorsqu’une demi-vie du noyau parent est plus courte qu’une demi-vie du noyau fille. Dans ce cas, le taux de production et le taux de désintégration de certains membres de la chaîne de désintégration ne peuvent pas être égaux.
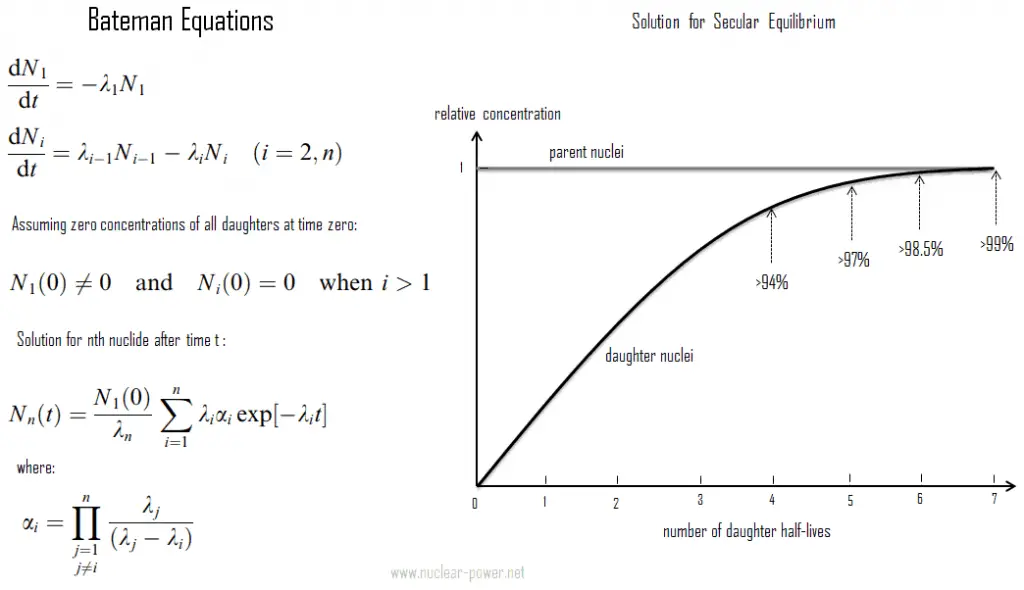
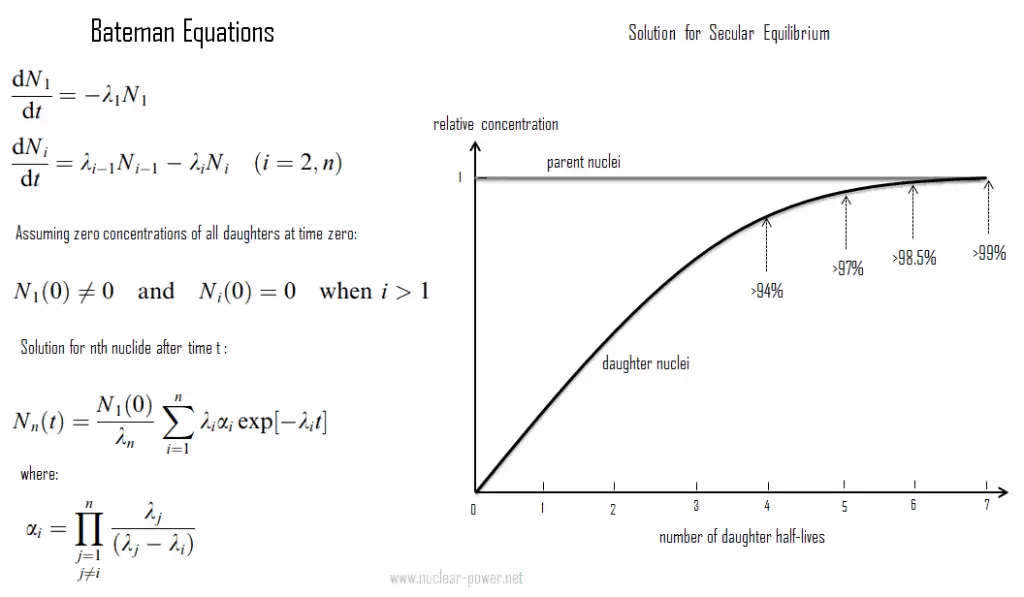
- L’équilibre radioactif séculaire existe lorsque le noyau parent a une demi-vie extrêmement longue. Ce type d’équilibre est particulièrement important dans la nature. Au cours des 4,5 milliards d’années de l’histoire de la Terre, notamment l’uranium 238, l’uranium 235 et le thorium 232 et les membres de leurs chaînes de désintégration ont atteint des équilibres radioactifs entre le noyau parent et les différents descendants.
- Un équilibre radioactif transitoire existe lorsqu’une demi-vie du noyau parent est plus longue qu’une demi-vie du noyau fille. Dans ce cas, le nucléide parent et le nucléide fille se désintègrent essentiellement à la même vitesse.
Équilibre séculaire
L’équilibre radioactif séculaire existe lorsque le noyau parent a une demi-vie extrêmement longue . L’équilibre séculaire est typique des séries radioactives naturelles , telles que la série thorium ou la série uranium . Pour la série d’uranium avec de l’uranium-238 (avec une demi-vie de 4,47 milliards d’années), où tous les éléments de la chaîne sont en équilibre séculaire , chacun des descendants a atteint un niveau d’équilibre et toute décomposition au rythme défini par le parent d’origine. La seule exception est l’élément stable final (plomb-206) à l’extrémité de la chaîne. Son nombre d’atomes augmente constamment. En tout cas, un équilibre radioactifn’est pas établie immédiatement, mais elle n’a lieu qu’après une période de transition . Cette période est de l’ordre de quelques demi-vies du noyau à longue durée de vie dans la chaîne de désintégration ( 234 U pour la série uranium ; 231 Pa pour la série actinium). Dans le cas de chaînes de désintégration radioactives, un équilibre radioactif peut être établi entre chaque membre de la chaîne de désintégration.
Comme on peut le voir, l’ équilibre séculaire est particulièrement important dans la nature. Au cours des 4,5 milliards d’années de l’histoire de la Terre, en particulier l’uranium 238, l’uranium 235 et le thorium 232 et les membres de leurs chaînes de désintégration ont atteint des équilibres radioactifsentre le noyau parent et les différents descendants. Les demi-vies de tous leurs descendants sont toutes extrêmement variables et il est difficile de représenter une gamme d’échelles de temps allant de quelques secondes à des millions d’années. Comme les radio-isotopes filles ont des demi-vies différentes, l’équilibre séculaire est atteint après un certain temps. Dans la longue chaîne de désintégration d’un élément naturellement radioactif, comme l’uranium-238, où tous les éléments de la chaîne sont en équilibre séculaire, chacun des descendants a accumulé une quantité d’équilibre et toute décomposition au taux fixé par le parent d’origine. Si et quand l’équilibre est atteint, chaque isotope fille successif est présent en proportion directe de sa demi-vie (ou de sa constante de désintégration).
Son activité étant inversement proportionnelle à sa demi-vie , chaque nucléide de la chaîne de désintégration apporte finalement autant de transformations individuelles que la tête de chaîne. La cascade radioactive dans l’équilibre séculaire influence de manière significative la radioactivité ( désintégrations par seconde ) des échantillons naturels et des matériaux naturels. Tous les descendants sont présents, au moins de façon transitoire, dans n’importe quel échantillon naturel, qu’il soit métallique, composé ou minéral. Par exemple, l’uranium 238 pur est faiblement radioactif (proportionnel à sa longue demi-vie), mais un minerai d’uranium est environ 13 fois plus radioactif (environ 13 descendants dans la chaîne de désintégration) que le métal d’uranium 238 pur en raison de ses isotopes filles (par exemple le radon, le radium, etc.) qu’il contient. Non seulement les isotopes du radium instables sont d’importants émetteurs de radioactivité, mais en tant que prochaine étape de la chaîne de désintégration, ils génèrent également du radon, un gaz radioactif naturel lourd et inerte. De plus, la chaleur de désintégration de l’uranium et de ses produits de désintégration (par exemple le radon, le radium, etc.) contribue au réchauffement du cœur de la Terre. Avec le thorium et le potassium-40 dans le manteau terrestre, on pense que ces éléments sont la principale source de chaleur qui maintient le noyau liquide de la Terre.
L’ équilibre séculaire peut parfois être perturbé lorsque l’un des noyaux intermédiaires quitte l’échantillon (par exemple le radon libéré du sol) où ses ancêtres sont confinés. Ces perturbations locales sont importantes à prendre en compte dans l’utilisation des techniques de datation. La perturbation de l’équilibre séculaire influe également sur la radioactivité du combustible nucléaire frais. La plupart des REP utilisent le combustible d’uranium , qui est sous forme de dioxyde d’uranium . Mais ce dioxyde d’uranium doit être chimiquement purifié et la majeure partie de sa chaîne de désintégration n’est pas présente dans le combustible nucléaire frais.
Équilibre radioactif de l’uranium 234
L’isotope de l’uranium-234 fait partie de la série de l’uranium. Cet isotope a une demi-vie de seulement 2,46 × 10 5 ans et n’appartient donc pas aux nucléides primordiaux (contrairement à 235 U et 238 U ). D’autre part, cet isotope est encore présent dans la croûte terrestre, mais cela est dû au fait 234 U est un produit de désintégration indirecte de 238 U . 238 U se désintègre via la désintégration alpha en 234 U. 234 U se désintègre via la désintégration alpha en 230Th, sauf une très petite fraction (de l’ordre de ppm) de noyaux qui se désintègre par fission spontanée.
Dans un échantillon naturel d’uranium, ces noyaux sont présents dans les proportions inaltérables de l’ équilibre radioactif de la filiation 238 U dans un rapport d’un atome de 234 U pour environ 18 500 noyaux de 238 U. Du fait de cet équilibre, ces deux les isotopes ( 238 U et 234 U) contribuent également à la radioactivité de l’uranium naturel.
Équilibre radioactif transitoire
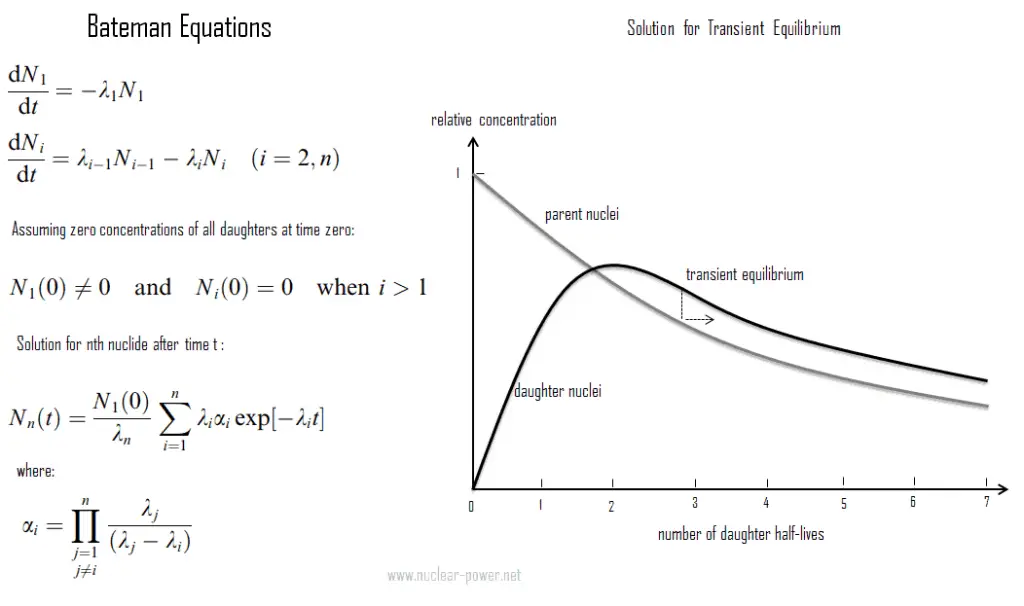
L’ équilibre radioactif transitoire existe lorsqu’une demi-vie du noyau parent est plus longue qu’une demi-vie du noyau fille, mais que la concentration des noyaux parents diminue de manière significative dans le temps. Dans ce cas, le nucléide parent et le nucléide fille peuvent se désintégrer essentiellement à la même vitesse, mais les deux concentrations de nucléides diminuent à mesure que la concentration des noyaux parents diminue. Contrairement à l’équilibre séculaire, la demi-vie des noyaux filles n’est pas négligeable par rapport à la demi-vie du parent.
Un exemple de ce type de processus de désintégration des composés est un générateur de technétium-99m produisant du technétium-99m pour les procédures de diagnostic en médecine nucléaire à partir du molybdène-99. La courte demi-vie de 6 heures du technétium-99m rend le stockage impossible et rendrait le transport très coûteux. Par conséquent, à des fins médicales, le molybdène 99 est utilisé pour produire du technétium 99m. Ces deux isotopes sont en équilibre transitoire. La constante de désintégration du molybdène-99 est considérablement plus petite que la constante de désintégration du technétium-99m. Bien que la constante de désintégration du molybdène 99 soit plus petite, le taux réel de désintégration est initialement supérieur à celui du molybdène 99 en raison de la grande différence dans leurs concentrations initiales. À mesure que la concentration de la fille augmente, le taux de désintégration de la fille s’approche et finit par correspondre au taux de désintégration du parent. Lorsque cela se produit, on dit qu’ils sont à l’ équilibre transitoire . Dans le cas d’un générateur de technétium 99m, l’équilibre transitoire se produit après environ quatre demi-vies. Aujourd’hui, le technétium-99m est l’élément le plus utilisé en médecine nucléaire et est utilisé dans une grande variété d’études d’imagerie en médecine nucléaire.
De plus, l’équilibre transitoire peut parfois être perturbé lorsque l’un des noyaux intermédiaires quitte l’échantillon où ses ancêtres sont confinés.
Équilibre radioactif transitoire avec source – Exemple
Un exemple particulier d’équilibre radioactif est les concentrations d’iode 135 et de xénon 135 dans un réacteur nucléaire , mais dans ce cas, la combustion du xénon doit être prise en compte. Notez que, dans ce cas particulier, la demi-vie du noyau parent est plus courte que la demi-vie du noyau fille. La production et l’élimination du xénon peuvent être caractérisées par les équations différentielles suivantes :
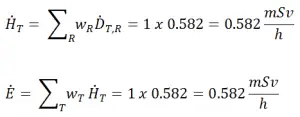 Lorsque le taux de production d’iode est égal au taux d’élimination de l’iode, l’ équilibre existe. Cet équilibre est également appelé «réservoir de xénon 135», car tout cet iode doit subir une désintégration au xénon. A l’équilibre, la concentration en iode reste constante et est désignée N I (eq) . L’équation suivante pour la concentration d’équilibre en iode peut être déterminée à partir de l’équation précédente en fixant le dN I / dt = 0 . Étant donné que la concentration d’iode à l’équilibre est proportionnelle à la vitesse de réaction de fission, elle est également proportionnelle au niveau de puissance du réacteur .
Lorsque le taux de production d’iode est égal au taux d’élimination de l’iode, l’ équilibre existe. Cet équilibre est également appelé «réservoir de xénon 135», car tout cet iode doit subir une désintégration au xénon. A l’équilibre, la concentration en iode reste constante et est désignée N I (eq) . L’équation suivante pour la concentration d’équilibre en iode peut être déterminée à partir de l’équation précédente en fixant le dN I / dt = 0 . Étant donné que la concentration d’iode à l’équilibre est proportionnelle à la vitesse de réaction de fission, elle est également proportionnelle au niveau de puissance du réacteur .
Lorsque le taux de production de xénon 135 est égal au taux d’élimination , l’ équilibre existe également pour le xénon . La concentration en xénon reste constante et est désignée N Xe (eq) . L’équation suivante (1) pour la concentration d’équilibre au xénon peut être déterminée à partir de l’équation précédente en fixant le dN Xe / dt = 0 . Pour que le xénon 135 soit en équilibre, l’iode 135 doit également être en équilibre. La substitution de l’expression de concentration d’iode 135 à l’équilibre dans l’équation du xénon d’équilibre (1) donne les résultats suivants (2).
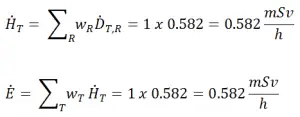 D’après cette équation, on peut voir que la valeur d’équilibre du xénon 135 augmente à mesure que la puissance augmente, car le numérateur est proportionnel à la vitesse de réaction de fission . Mais le flux thermique est également au dénominateur. Par conséquent, comme le flux thermique dépasse une certaine valeur, la combustion du xénon commence à dominer, et à environ 10 15 neutrons.cm -2 .s -1 , la concentration en xénon-135 approche une valeur limite. Les concentrations d’équilibre d’iode 135 et de xénon 135 en fonction du flux neutronique sont illustrées dans la figure suivante.
D’après cette équation, on peut voir que la valeur d’équilibre du xénon 135 augmente à mesure que la puissance augmente, car le numérateur est proportionnel à la vitesse de réaction de fission . Mais le flux thermique est également au dénominateur. Par conséquent, comme le flux thermique dépasse une certaine valeur, la combustion du xénon commence à dominer, et à environ 10 15 neutrons.cm -2 .s -1 , la concentration en xénon-135 approche une valeur limite. Les concentrations d’équilibre d’iode 135 et de xénon 135 en fonction du flux neutronique sont illustrées dans la figure suivante.
Équations de Bateman
En physique, les équations de Bateman sont un ensemble d’équations différentielles de premier ordre, qui décrivent l’évolution dans le temps des concentrations de nucléides subissant une chaîne de désintégration en série ou linéaire. Le modèle a été formulé par Ernest Rutherford en 1905 et la solution analytique pour le cas de la désintégration radioactive dans une chaîne linéaire a été fournie par Harry Bateman en 1910. Ce modèle peut également être utilisé dans les codes d’épuisement nucléaire pour résoudre les problèmes de transmutation et de désintégration nucléaire.
Par exemple, ORIGEN est un système de code informatique pour calculer l’accumulation, la désintégration et le traitement des matières radioactives. ORIGEN utilise une méthode exponentielle matricielle pour résoudre un grand système d’équations différentielles ordinaires couplées, linéaires, du premier ordre (similaires aux équations de Bateman ) avec des coefficients constants.
Les équations de Bateman pour le cas de désintégration radioactive de séries de n-nucléides en chaîne linéaire décrivant les concentrations de nucléides sont les suivantes:
Équations de Bateman pour la transmutation nucléaire
Comme cela a été écrit, ce modèle peut également être utilisé dans les codes d’épuisement nucléaire pour résoudre également les problèmes de transmutation et de désintégration nucléaire . En cas de transmutation, les constantes de désintégration qui régissent les équations de Bateman pour un cas de désintégration sont remplacées par des constantes de transmutation. Par la constante de transmutation λ i, j on comprend probabilité de la i ème production nucléide par unité de temps à partir de la j ème destruction nucléide, à la suite de l’ interaction nucléaire avec tout le spectre des particules en interaction ou en raison de la désintégration nucléaire naturel.
Ces équations sont généralement utilisées pour l’évolution exacte des changements isotopiques dans le combustible nucléaire pendant l’épuisement du combustible. L’épuisement du carburant est généralement modélisé mathématiquement comme un ensemble d’équations différentielles appelées équations d’ évolution .
Référence spéciale: Jerzy Cetnar, Solution générale des équations de Bateman pour les transmutations nucléaires. Annals of Nuclear Energy 33 (2006). Janvier 2006.
……………………………………………………………………………………………………………………………….
Cet article est basé sur la traduction automatique de l’article original en anglais. Pour plus d’informations, voir l’article en anglais. Pouvez vous nous aider Si vous souhaitez corriger la traduction, envoyez-la à l’adresse: [email protected] ou remplissez le formulaire de traduction en ligne. Nous apprécions votre aide, nous mettrons à jour la traduction le plus rapidement possible. Merci