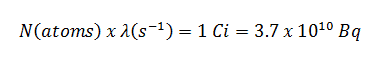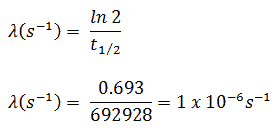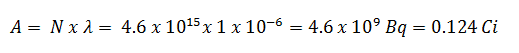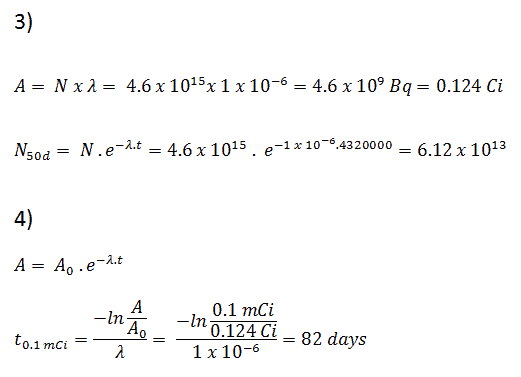Qu’est-ce que le calcul de la radioactivité à partir de la constante de désintégration – Définition

Constante de désintégration et radioactivité

La relation entre la demi-vie et la quantité de radionucléide nécessaire pour donner une activité d’un curie est illustrée sur la figure. Cette quantité de matière peut être calculée en utilisant λ , qui est la constante de désintégration de certains nucléides:

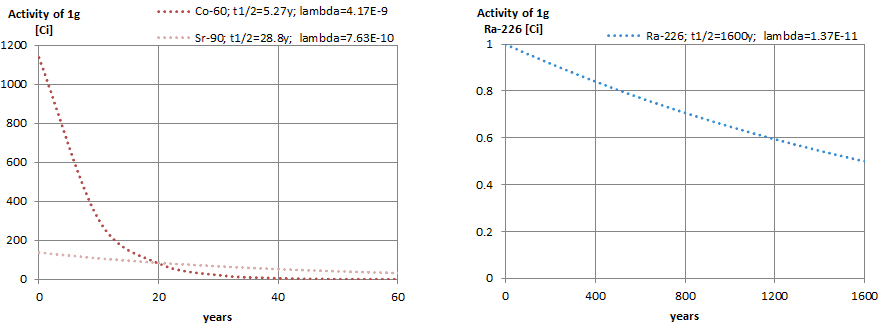
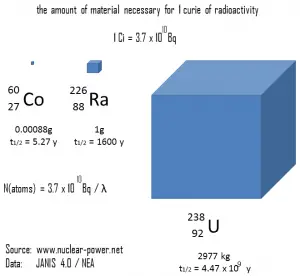La figure suivante illustre la quantité de matière nécessaire pour 1 curie de radioactivité. Il est évident que plus la demi-vie est longue, plus la quantité de radionucléide nécessaire pour produire la même activité est importante. Bien sûr, la substance à longue durée de vie restera radioactive pendant beaucoup plus longtemps. Comme on peut le voir, la quantité de matière nécessaire pour 1 curie de radioactivité peut varier d’une quantité trop petite pour être vue (0,00088 gramme de cobalt-60), à travers 1 gramme de radium-226, à près de trois tonnes d’ uranium-238 .

Exemple – Calcul de la radioactivité

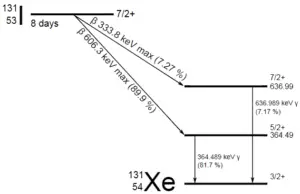Un échantillon de matériau contient 1 mikrogramme d’iode 131. Il convient de noter que l’iode 131 joue un rôle majeur en tant qu’isotope radioactif présent dans les produits de fission nucléaire et qu’il contribue de façon importante aux risques pour la santé lorsqu’il est rejeté dans l’atmosphère lors d’un accident. L’iode-131 a une demi-vie de 8,02 jours.

Calculer:

1. Le nombre d’atomes d’iode-131 initialement présents.
2. L’activité de l’iode 131 dans les curies.
3. Le nombre d’atomes d’iode-131 qui resteront dans 50 jours.
4. Temps nécessaire à l’activité pour atteindre 0,1 mCi.

Solution:

1. Le nombre d’atomes d’iode-131 peut être déterminé en utilisant la masse isotopique comme ci-dessous.

N _I-131 = m _I-131 . N _A / M _I-131

N _I-131 = (1 μg) x (6,02 × 10 ²³ noyaux / mol) / (130,91 g / mol)

N _I-131 = 4,6 x 10 ¹⁵ noyaux

2. L’activité de l’iode 131 dans les curies peut être déterminée en utilisant sa constante de désintégration :

L’iode 131 a une demi-vie de 8,02 jours (692928 s) et donc sa constante de désintégration est:

En utilisant cette valeur pour la constante de désintégration, nous pouvons déterminer l’activité de l’échantillon:

3) et 4) Le nombre d’atomes d’iode-131 qui resteront dans 50 jours (N _50d ) et le temps qu’il faudra pour que l’activité atteigne 0,1 mCi peuvent être calculés en utilisant la loi de décroissance:

Comme on peut le voir, après 50 jours, le nombre d’atomes d’iode 131 et donc l’activité sera environ 75 fois plus faible. Après 82 jours, l’activité sera environ 1200 fois plus faible. Par conséquent, le temps de dix demi-vies (facteur 2 ¹⁰ = 1024) est largement utilisé pour définir l’activité résiduelle.