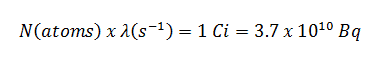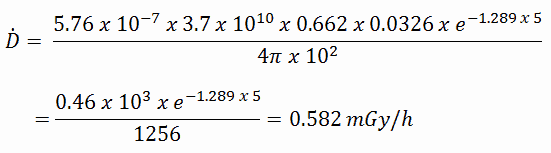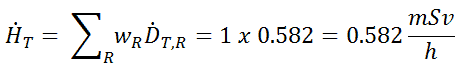 Im Strahlenschutz ist das Sievert eine abgeleitete Einheit aus Äquivalentdosis und effektiver Dosis. Das Sievert repräsentiert den äquivalenten biologischen Effekt der Ablagerung eines Joules Gammastrahlenenergie in einem Kilogramm menschlichem Gewebe. Die Einheit Sievert ist für den Strahlenschutz von Bedeutung und wurde nach dem schwedischen Wissenschaftler Rolf Sievert benannt, der einen Großteil der frühen Arbeiten zur Dosimetrie in der Strahlentherapie durchgeführt hat.
Im Strahlenschutz ist das Sievert eine abgeleitete Einheit aus Äquivalentdosis und effektiver Dosis. Das Sievert repräsentiert den äquivalenten biologischen Effekt der Ablagerung eines Joules Gammastrahlenenergie in einem Kilogramm menschlichem Gewebe. Die Einheit Sievert ist für den Strahlenschutz von Bedeutung und wurde nach dem schwedischen Wissenschaftler Rolf Sievert benannt, der einen Großteil der frühen Arbeiten zur Dosimetrie in der Strahlentherapie durchgeführt hat.
Wie geschrieben wurde, wird das Sievert für Strahlendosismengen wie Äquivalentdosis und effektive Dosis verwendet. Die Äquivalentdosis (Symbol H T ) ist eine für einzelne Organe berechnete Dosismenge (Index T – Gewebe). Die äquivalente Dosis basiert auf der absorbierten Dosis eines Organs, angepasst an die Wirksamkeit der Strahlungsart . Äquivalentdosis ist das Symbol H gegeben T . Die SI – Einheit von H T ist die Sievert (Sv) oder aber rem (roentgen equivalent man) ist immer noch häufig verwendet ( 1 Sv = 100 rem ).
Sievert und Gray
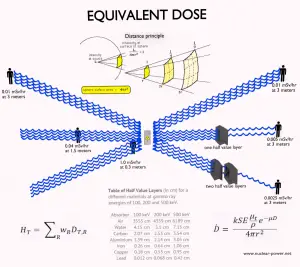
Zum Strahlenschutz wird die Energiedosis über ein Organ oder Gewebe T gemittelt und dieser Energiedosismittelwert für die Strahlungsqualität mit dem Strahlungsgewichtungsfaktor w R für die Art und Energie der auf das Organ einfallenden Strahlung gewichtet Körper. Der Strahlungsgewichtungsfaktor ist ein dimensionsloser Faktor zur Bestimmung der Äquivalentdosis aus der über ein Gewebe oder Organ gemittelten Energiedosis und basiert auf der Art der absorbierten Strahlung. Die resultierende gewichtete Dosis wurde als Organ- oder Gewebeäquivalentdosis bezeichnet:
Eine äquivalente Dosis von einem Sievert darstellt , dass die Menge der Strahlungsdosis , die äquivalent ist, in Bezug auf den angegebenen biologischen Schäden , zu einem Gray von Röntgenstrahlen oder Gammastrahlen . Eine Dosis von einem Sv, die durch Gammastrahlung verursacht wird, entspricht einer Energiedeposition von einem Joule pro Kilogramm Gewebe. Das heißt, ein Sieb entspricht einem Gray von Gammastrahlen, die in einem bestimmten Gewebe abgelagert sind. Andererseits kann ein ähnlicher biologischer Schaden (ein Sievert) nur durch 1/20 der Alphastrahlung (aufgrund des hohen w R der Alphastrahlung) verursacht werden. Daher ist das Sievert keine physikalische Dosiseinheit. Beispielsweise führt eine absorbierte Dosis von 1 Gy durch Alpha-Partikel zu einer äquivalenten Dosis von 20 Sv. Dies mag paradox erscheinen. Dies impliziert, dass die Energie des einfallenden Strahlungsfeldes in Joule um den Faktor 20 angestiegen ist, wodurch die Gesetze der Energieerhaltung verletzt wurden . Dies ist jedoch nicht der Fall. Sievert wird aus der aufgenommenen Dosis der physikalischen Größe abgeleitet, berücksichtigt aber auch die biologische Wirksamkeit der Strahlung, die von der Strahlungsart und der Energie abhängt. Der Strahlungsgewichtungsfaktor bewirkt, dass das Sievert keine physikalische Einheit sein kann.
Ein Sieb ist eine große Menge der Äquivalentdosis. Eine Person, die eine Ganzkörperdosis von 1 Sv absorbiert hat, hat 1 Joule Energie in jedem kg Körpergewebe absorbiert (im Falle von Gammastrahlen).
In Industrie und Medizin gemessene äquivalente Dosen weisen gewöhnlich niedrigere Dosen als ein Sieb auf, und die folgenden Vielfachen werden häufig verwendet:
1 mSv (Millisievert) = 1E-3 Sv
1 uSv (Mikrosievert) = 1E-6 Sv
Die Umrechnungen von den SI-Einheiten in andere Einheiten lauten wie folgt:
- 1 Sv = 100 rem
- 1 mSv = 100 mrem
Strahlungsgewichtungsfaktoren – ICRP
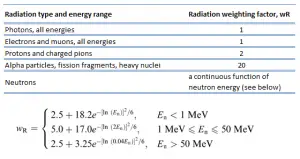
Für Photonen- und Elektronenstrahlung hat der Strahlungsgewichtungsfaktor unabhängig von der Energie der Strahlung den Wert 1 und für Alphastrahlung den Wert 20. Für Neutronenstrahlung ist der Wert energieabhängig und beträgt 5 bis 20.

2007 veröffentlichte ICRP eine neue Reihe von Strahlungsgewichtungsfaktoren (ICRP Publ. 103: Die Empfehlungen 2007 der Internationalen Strahlenschutzkommission). Diese Faktoren sind unten angegeben.
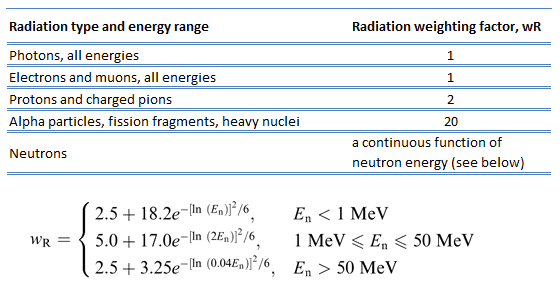
Wie in der Tabelle gezeigt, gilt aw R von 1 für alle Strahlungen mit niedrigem LET, dh Röntgen- und Gammastrahlen aller Energien sowie Elektronen und Myonen. Eine glatte Kurve, die als Annäherung betrachtet wird, wurde an die w R -Werte als Funktion der einfallenden Neutronenenergie angepasst . Beachten Sie, dass E n ist die Neutronenenergie in MeV.
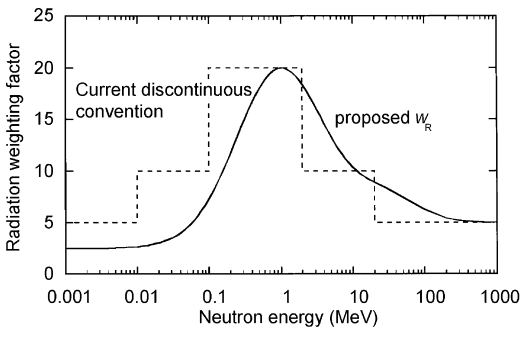
So führt beispielsweise eine von Alpha-Partikeln absorbierte Dosis von 1 Gy zu einer äquivalenten Dosis von 20 Sv, und es wird geschätzt, dass eine äquivalente Strahlungsdosis den gleichen biologischen Effekt hat wie eine gleiche absorbierte Dosis von Gammastrahlen bei einem Gewichtungsfaktor von 1.
Siehe auch: Qualitätsfaktor
Beispiele für Dosen in Sieverts
Wir müssen beachten, dass Strahlung überall um uns herum ist. In, um und über der Welt, in der wir leben. Es ist eine natürliche Energiekraft, die uns umgibt. Es ist ein Teil unserer natürlichen Welt, der seit der Geburt unseres Planeten hier ist. In den folgenden Punkten versuchen wir, enorme Bereiche der Strahlenexposition auszudrücken, die aus verschiedenen Quellen erhalten werden können.
- 0,05 µSv – Schlafen neben jemandem
- 0,09 µSv – Ein Jahr lang in einem Umkreis von 30 Meilen um ein Kernkraftwerk leben
- 0,1 µSv – Eine Banane essen
- 0,3 µSv – Ein Jahr lang in einem Umkreis von 50 Meilen um ein Kohlekraftwerk leben
- 10 µSv – Durchschnittliche Tagesdosis aus natürlichem Hintergrund
- 20 µSv – Röntgenaufnahme der Brust
- 40 µSv – Ein 5-stündiger Flugzeugflug
- 600 µSv – Mammographie
- 1 000 µSv – Dosisgrenze für einzelne Mitglieder der Öffentlichkeit, effektive Gesamtdosis pro Jahr
- 3 650 µSv – Durchschnittliche jährliche Dosis aus natürlichem Hintergrund
- 5 800 µSv – Brust-CT-Scan
- 10 000 µSv – Durchschnittliche jährliche Dosis aus natürlichem Hintergrund in Ramsar, Iran
- 20 000 µSv – Einzel-Ganzkörper-CT
- 175 000 µSv – Jährliche Dosis natürlicher Strahlung an einem Monazitstrand in der Nähe von Guarapari, Brasilien.
- 5 000 000 µSv – Dosis, die einen Menschen mit einem 50% igen Risiko innerhalb von 30 Tagen tötet (LD50 / 30), wenn die Dosis über einen sehr kurzen Zeitraum verabreicht wird .
Wie zu sehen ist, sind niedrige Dosen im Alltag üblich. Die vorherigen Beispiele können helfen, relative Größen zu veranschaulichen. Unter dem Gesichtspunkt der biologischen Konsequenzen ist es sehr wichtig, zwischen Dosen zu unterscheiden, die über kurze und längere Zeiträume erhalten werden . Eine „ akute Dosis “ tritt über einen kurzen und begrenzten Zeitraum auf, während eine „ chronische Dosis “ auftritt”Ist eine Dosis, die über einen längeren Zeitraum anhält, damit sie besser durch eine Dosisleistung beschrieben werden kann. Hohe Dosen neigen dazu, Zellen abzutöten, während niedrige Dosen dazu neigen, sie zu beschädigen oder zu verändern. Niedrige Dosen, die über lange Zeiträume verteilt sind, verursachen für kein Körperorgan ein unmittelbares Problem. Die Auswirkungen niedriger Strahlendosen treten auf der Ebene der Zelle auf, und die Ergebnisse werden möglicherweise über viele Jahre hinweg nicht beobachtet.
Berechnung der abgeschirmten Dosisleistung in Sieverts
Angenommen, die punktisotrope Quelle enthält 1,0 Ci von 137 Cs und hat eine Halbwertszeit von 30,2 Jahren . Es ist zu beachten, dass die Beziehung zwischen der Halbwertszeit und der Menge eines Radionuklids, die erforderlich ist, um eine Aktivität von einem Curie zu ergeben , unten gezeigt ist. Diese Materialmenge kann mit λ berechnet werden, der Zerfallskonstante bestimmter Nuklide:
Etwa 94,6 Prozent zerfallen durch Beta-Emission zu einem metastabilen Kernisomer von Barium: Barium-137m. Der Hauptphotonenpeak von Ba-137m beträgt 662 keV . Nehmen Sie für diese Berechnung an, dass alle Zerfälle diesen Kanal durchlaufen.
Berechnen Sie die primäre Photonendosisrate in Gray pro Stunde (Gy.h -1 ) an der Außenfläche eines 5 cm dicken Bleischilds . Dann berechnet die Äquivalentdosisleistung . Angenommen, dieses externe Strahlungsfeld durchdringt den gesamten Körper gleichmäßig . Die Primärphotonendosisrate vernachlässigt alle Sekundärteilchen. Angenommen, der effektive Abstand der Quelle vom Dosispunkt beträgt 10 cm . Wir werden auch annehmen, dass der Dosispunkt Weichgewebe ist und vernünftigerweise durch Wasser simuliert werden kann, und wir verwenden den Massenenergieabsorptionskoeffizienten für Wasser.
Siehe auch: Gammastrahlendämpfung
Siehe auch: Abschirmung von Gammastrahlen
Lösung:
Die Primärphotonendosisrate wird exponentiell abgeschwächt , und die Dosisrate von Primärphotonen unter Berücksichtigung der Abschirmung ist gegeben durch:
Wie zu sehen ist, berücksichtigen wir den Aufbau von Sekundärstrahlung nicht. Wenn Sekundärteilchen erzeugt werden oder wenn die Primärstrahlung ihre Energie oder Richtung ändert, ist die effektive Dämpfung viel geringer. Diese Annahme unterschätzt im Allgemeinen die wahre Dosisleistung, insbesondere für dicke Schilde und wenn der Dosispunkt nahe an der Schildoberfläche liegt, aber diese Annahme vereinfacht alle Berechnungen. In diesem Fall ist die tatsächliche Dosisleistung (mit dem Aufbau von Sekundärstrahlung) mehr als doppelt so hoch.
Um die absorbierte Dosisleistung zu berechnen , müssen wir in der Formel Folgendes verwenden:
- k = 5,76 · 10 & supmin; & sup7;
- S = 3,7 × 10 10 s –1
- E = 0,662 MeV
- μ t / ρ = 0,0326 cm 2 / g (Werte sind bei NIST erhältlich)
- μ = 1,289 cm -1 (Werte sind bei NIST erhältlich)
- D = 5 cm
- r = 10 cm
Ergebnis:
Die resultierende absorbierte Dosisrate in Gray pro Stunde beträgt dann:
Da der Strahlungsgewichtungsfaktor für Gammastrahlen gleich eins ist und wir das einheitliche Strahlungsfeld angenommen haben, können wir die äquivalente Dosisrate direkt aus der absorbierten Dosisrate berechnen als:
Wenn wir den Aufbau von Sekundärstrahlung berücksichtigen wollen, müssen wir den Aufbaufaktor einbeziehen. Die erweiterte Formel für die Dosisleistung lautet dann:
……………………………………………………………………………………………………………………………….
Dieser Artikel basiert auf der maschinellen Übersetzung des englischen Originalartikels. Weitere Informationen finden Sie im Artikel auf Englisch. Sie können uns helfen. Wenn Sie die Übersetzung korrigieren möchten, senden Sie diese bitte an: [email protected] oder füllen Sie das Online-Übersetzungsformular aus. Wir bedanken uns für Ihre Hilfe und werden die Übersetzung so schnell wie möglich aktualisieren. Danke.