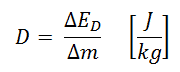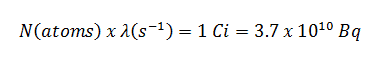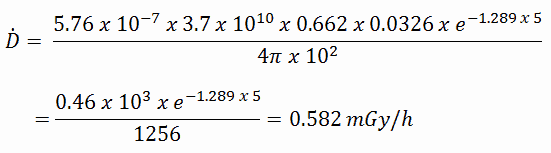Die Energiedosis ist definiert als die Energiemenge, die durch ionisierende Strahlung in einer Substanz abgegeben wird. Energiedosis wird das Symbol gegeben D . Die Energiedosis wird normalerweise in einer Einheit gemessen, die als Gray (Gy) bezeichnet wird und vom SI-System abgeleitet ist. Gelegentlich wird auch die Nicht-SI-Einheit rad verwendet, überwiegend in den USA.
Einheiten der Energiedosis:
- Gray . Eine Dosis von einem Gray entspricht einer Energieeinheit (Joule), die in einem Kilogramm eines Stoffes gespeichert ist.
- RAD . Eine Dosis von einem Rad entspricht der Ablagerung von einhundert Erg Energie in einem Gramm eines beliebigen Materials.
Gray – Einheit der Energiedosis
Eine Dosis von einem Gray entspricht einer Energieeinheit (Joule), die in einem Kilogramm eines Stoffes gespeichert ist. Diese Einheit wurde zu Ehren von Louis Harold Gray benannt , der einer der großen Pioniere der Strahlenbiologie war. Ein Gray ist eine große Menge der Energiedosis. Eine Person, die eine Ganzkörperdosis von 1 Gy aufgenommen hat, hat pro kg Körpergewebe ein Joule Energie aufgenommen.
Energiedosis, die in der Industrie gemessen werden (außer in der Nuklearmedizin), weisen normalerweise niedrigere Dosen als ein Gray auf, und die folgenden Vielfachen werden häufig verwendet:
1 mGy (Milligray) = 1E-3 Gy
1 µGy (Mikrogray) = 1E-6 Gy
Die Umrechnungen von SI-Einheiten in andere Einheiten lauten wie folgt:
- 1 Gy = 100 rad
- 1 mGy = 100 mrad
Das Gray und das Rad sind physikalische Einheiten. Sie beschreiben die physikalische Wirkung der einfallenden Strahlung (dh die pro kg abgelagerte Energiemenge), sagen jedoch nichts über die biologischen Folgen einer solchen Energiedeposition in lebendem Gewebe aus.
Beispiele für Energiedosis in Gray
Wir müssen beachten, dass Strahlung überall um uns herum ist. In, um und über der Welt, in der wir leben. Es ist eine natürliche Energiekraft, die uns umgibt. Es ist ein Teil unserer natürlichen Welt, der seit der Geburt unseres Planeten hier ist. In den folgenden Punkten versuchen wir, enorme Bereiche der Strahlenexposition auszudrücken, die aus verschiedenen Quellen erhalten werden können.
- 0,05 µGy – Schlafen neben jemandem
- 0,09 µGy – Ein Jahr lang in einem Umkreis von 30 Meilen um ein Kernkraftwerk leben
- 0,1 µGy – Eine Banane essen
- 0,3 µGy – Ein Jahr lang in einem Umkreis von 50 Meilen um ein Kohlekraftwerk leben
- 10 µGy – Durchschnittliche Tagesdosis aus natürlichem Hintergrund
- 20 µGy – Röntgenaufnahme der Brust
- 40 µGy – Ein 5-stündiger Flugzeugflug
- 600 µGy – Mammographie
- 1 000 µGy – Dosisgrenze für einzelne Mitglieder der Öffentlichkeit, effektive Gesamtdosis pro Jahr
- 3 650 µGy – Durchschnittliche jährliche Dosis aus natürlichem Hintergrund
- 5 800 µGy – Brust-CT-Scan
- 10 000 µGy – Durchschnittliche jährliche Dosis aus natürlichem Hintergrund in Ramsar, Iran
- 20 000 µGy – Einzel-Ganzkörper-CT
- 175 000 µGy – Jährliche Dosis natürlicher Strahlung an einem Monazitstrand in der Nähe von Guarapari, Brasilien.
- 5 000 000 µGy – Dosis, die einen Menschen mit einem 50% igen Risiko innerhalb von 30 Tagen tötet (LD50 / 30), wenn die Dosis über einen sehr kurzen Zeitraum verabreicht wird .
Wie zu sehen ist, sind niedrige Dosen im Alltag üblich. Die vorherigen Beispiele können helfen, relative Größen zu veranschaulichen. Unter dem Gesichtspunkt der biologischen Konsequenzen ist es sehr wichtig, zwischen Dosen zu unterscheiden, die über kurze und längere Zeiträume erhalten werden . Eine „ akute Dosis “ tritt über einen kurzen und begrenzten Zeitraum auf, während eine „ chronische Dosis “ auftritt”Ist eine Dosis, die über einen längeren Zeitraum anhält, damit sie besser durch eine Dosisleistung beschrieben werden kann. Hohe Dosen neigen dazu, Zellen abzutöten, während niedrige Dosen dazu neigen, sie zu beschädigen oder zu verändern. Niedrige Dosen, die über lange Zeiträume verteilt sind, verursachen für kein Körperorgan ein unmittelbares Problem. Die Auswirkungen niedriger Strahlendosen treten auf der Ebene der Zelle auf, und die Ergebnisse werden möglicherweise über viele Jahre hinweg nicht beobachtet.
Berechnung der abgeschirmten Dosisrate in Gray
Angenommen, die punktisotrope Quelle enthält 1,0 Ci von 137 Cs und hat eine Halbwertszeit von 30,2 Jahren . Es ist zu beachten, dass die Beziehung zwischen der Halbwertszeit und der Menge eines Radionuklids, die erforderlich ist, um eine Aktivität von einem Curie zu ergeben , unten gezeigt ist. Diese Materialmenge kann mit λ berechnet werden, der Zerfallskonstante bestimmter Nuklide:
Etwa 94,6 Prozent zerfallen durch Beta-Emission zu einem metastabilen Kernisomer von Barium: Barium-137m. Der Hauptphotonenpeak von Ba-137m beträgt 662 keV . Nehmen Sie für diese Berechnung an, dass alle Zerfälle diesen Kanal durchlaufen.
Berechnen Sie die primäre Photonendosisrate in Gray pro Stunde (Gy.h -1 ) an der Außenfläche eines 5 cm dicken Bleischilds . Die Primärphotonendosisrate vernachlässigt alle Sekundärteilchen. Angenommen, der effektive Abstand der Quelle vom Dosispunkt beträgt 10 cm . Wir werden auch annehmen, dass der Dosispunkt Weichgewebe ist und vernünftigerweise durch Wasser simuliert werden kann, und wir verwenden den Massenenergieabsorptionskoeffizienten für Wasser.
Siehe auch: Gammastrahlendämpfung
Siehe auch: Abschirmung von Gammastrahlen
Lösung:
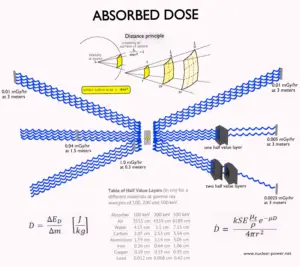
Die Primärphotonendosisrate wird exponentiell abgeschwächt , und die Dosisrate von Primärphotonen unter Berücksichtigung der Abschirmung ist gegeben durch:
Wie zu sehen ist, berücksichtigen wir den Aufbau von Sekundärstrahlung nicht. Wenn Sekundärteilchen erzeugt werden oder wenn die Primärstrahlung ihre Energie oder Richtung ändert, ist die effektive Dämpfung viel geringer. Diese Annahme unterschätzt im Allgemeinen die wahre Dosisleistung, insbesondere für dicke Abschirmungen und wenn der Dosispunkt nahe an der Abschirmoberfläche liegt, aber diese Annahme vereinfacht alle Berechnungen. In diesem Fall ist die tatsächliche Dosisleistung (mit dem Aufbau von Sekundärstrahlung) mehr als doppelt so hoch.
Um die Energiedosisleistung zu berechnen , müssen wir in der Formel Folgendes verwenden:
- k = 5,76 · 10 & supmin; & sup7;
- S = 3,7 × 10 10 s –1
- E = 0,662 MeV
- μ t / ρ = 0,0326 cm 2 / g (Werte sind bei NIST erhältlich)
- μ = 1,289 cm -1 (Werte sind bei NIST erhältlich)
- D = 5 cm
- r = 10 cm
Ergebnis:
Die resultierende Energiedosisrate in Gray pro Stunde beträgt dann:
Wenn wir den Aufbau von Sekundärstrahlung berücksichtigen wollen, müssen wir den Aufbaufaktor einbeziehen. Die erweiterte Formel für die Dosisleistung lautet dann:
