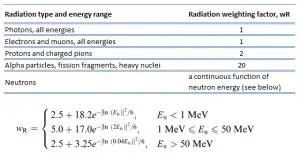
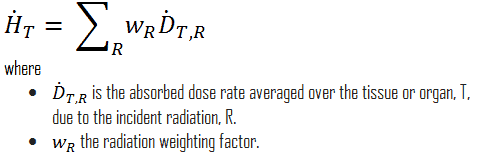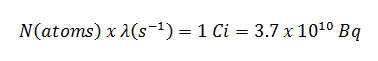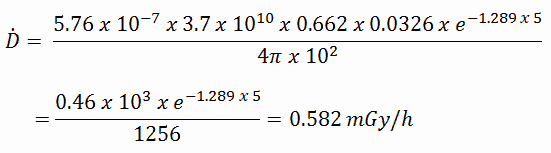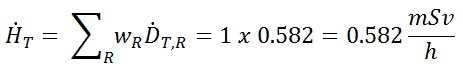What is Equivalent Dose - Formula - Equation

Equivalent Dose Formula – Equation. This article summarizes key formulas and equations, that can be used for equivalent dose calculations. Radiation Dosimetry

Equivalent dose (symbol H_T) is a dose quantity calculated for individual organs (index T – tissue). Equivalent dose is based on the absorbed dose to an organ, adjusted to account for the effectiveness of the type of radiation. Equivalent dose is given the symbol H_T. The SI unit of H_T is the sievert (Sv) or but rem (roentgen equivalent man) is still commonly used (1 Sv = 100 rem). The weighted dose was designated as the organ- or tissue equivalent dose:

A dose of one Sv caused by gamma radiation is equivalent to an energy deposition of one joule in a kilogram of a tissue. That means one sievert is equivalent to one gray of gamma rays deposited in certain tissue. On the other hand, similar biological damage (one sievert) can be caused only by 1/20 gray of alpha radiation.

One sievert is a large amount of equivalent dose. A person who has absorbed a whole body dose of 1 Sv has absorbed one joule of energy in each kg of body tissue (in case of gamma rays).

Equivalent doses measured in industry and medicine often have usually lower doses than one sievert, and the following multiples are often used:

1 mSv (millisievert) = 1E-3 Sv

1 µSv (microsievert) = 1E-6 Sv

Conversions from the SI units to other units are as follows:

1 Sv = 100 rem
1 mSv = 100 mrem

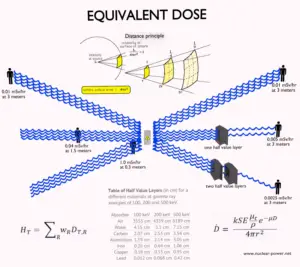
Equivalent Dose Rate

The equivalent dose rate is the rate at which an equivalent dose is received. It is a measure of radiation dose intensity (or strength). The equivalent dose rate is therefore defined as:

In conventional units, it is measured in mSv/sec, Sv/hr, mrem/sec or rem/hr. Since the amount of radiation exposure depends directly (linearly) on the time people spend near the source of radiation, the absorbed dose is equal to the strength of the radiation field (dose rate) multiplied by the length of time spent in that field. The example above indicates a person could expect to receive a dose of 25 millirems by staying in a 50 millirems/hour field for thirty minutes.

Calculation of Shielded Dose Rate

Assume the point isotropic source which contains 1.0 Ci of ¹³⁷Cs, which has a half-life of 30.2 years. Note that the relationship between half-life and the amount of a radionuclide required to give an activity of one curie is shown below. This amount of material can be calculated using λ, which is the decay constant of certain nuclide:

About 94.6 percent decays by beta emission to a metastable nuclear isomer of barium: barium-137m. The main photon peak of Ba-137m is 662 keV. For this calculation, assume that all decays go through this channel.

Calculate the primary photon dose rate, in gray per hour (Gy.h^-1), at the outer surface of a 5 cm thick lead shield. Then calculate the equivalent dose rate. Assume that this external radiation field penetrate uniformly through the whole body. Primary photon dose rate neglects all secondary particles. Assume that the effective distance of the source from the dose point is 10 cm. We shall also assume that the dose point is soft tissue and it can reasonably be simulated by water and we use the mass energy absorption coefficient for water.

See also: Shielding of Gamma Rays

Solution:

The primary photon dose rate is attenuated exponentially, and the dose rate from primary photons, taking account of the shield, is given by:

As can be seen, we do not account for the buildup of secondary radiation. If secondary particles are produced or if the primary radiation changes its energy or direction, then the effective attenuation will be much less. This assumption generally underestimates the true dose rate, especially for thick shields and when the dose point is close to the shield surface, but this assumption simplifies all calculations. For this case the true dose rate (with the buildup of secondary radiation) will be more than two times higher.

To calculate the absorbed dose rate, we have to use in the formula:

k = 5.76 x 10^-7
S = 3.7 x 10¹⁰ s^-1
E = 0.662 MeV
μ_t/ρ = 0.0326 cm²/g (values are available at NIST)
μ = 1.289 cm^-1 (values are available at NIST)
D = 5 cm
r = 10 cm

Result:

The resulting absorbed dose rate in grays per hour is then:

Since the radiation weighting factor for gamma rays is equal to one and we have assumed the uniform radiation field, we can directly calculate the equivalent dose rate from the absorbed dose rate as:

If we want to account for the buildup of secondary radiation, then we have to include the buildup factor. The extended formula for the dose rate is then:

——–

References:

Radiation Protection:

Knoll, Glenn F., Radiation Detection and Measurement 4th Edition, Wiley, 8/2010. ISBN-13: 978-0470131480.
Stabin, Michael G., Radiation Protection and Dosimetry: An Introduction to Health Physics, Springer, 10/2010. ISBN-13: 978-1441923912.
Martin, James E., Physics for Radiation Protection 3rd Edition, Wiley-VCH, 4/2013. ISBN-13: 978-3527411764.
U.S.NRC, NUCLEAR REACTOR CONCEPTS
U.S. Department of Energy, Nuclear Physics and Reactor Theory. DOE Fundamentals Handbook, Volume 1 and 2. January 1993.

Nuclear and Reactor Physics:

J. R. Lamarsh, Introduction to Nuclear Reactor Theory, 2nd ed., Addison-Wesley, Reading, MA (1983).
J. R. Lamarsh, A. J. Baratta, Introduction to Nuclear Engineering, 3d ed., Prentice-Hall, 2001, ISBN: 0-201-82498-1.
W. M. Stacey, Nuclear Reactor Physics, John Wiley & Sons, 2001, ISBN: 0- 471-39127-1.
Glasstone, Sesonske. Nuclear Reactor Engineering: Reactor Systems Engineering, Springer; 4th edition, 1994, ISBN: 978-0412985317
W.S.C. Williams. Nuclear and Particle Physics. Clarendon Press; 1 edition, 1991, ISBN: 978-0198520467
G.R.Keepin. Physics of Nuclear Kinetics. Addison-Wesley Pub. Co; 1st edition, 1965
Robert Reed Burn, Introduction to Nuclear Reactor Operation, 1988.
U.S. Department of Energy, Nuclear Physics and Reactor Theory. DOE Fundamentals Handbook, Volume 1 and 2. January 1993.
Paul Reuss, Neutron Physics. EDP Sciences, 2008. ISBN: 978-2759800414.