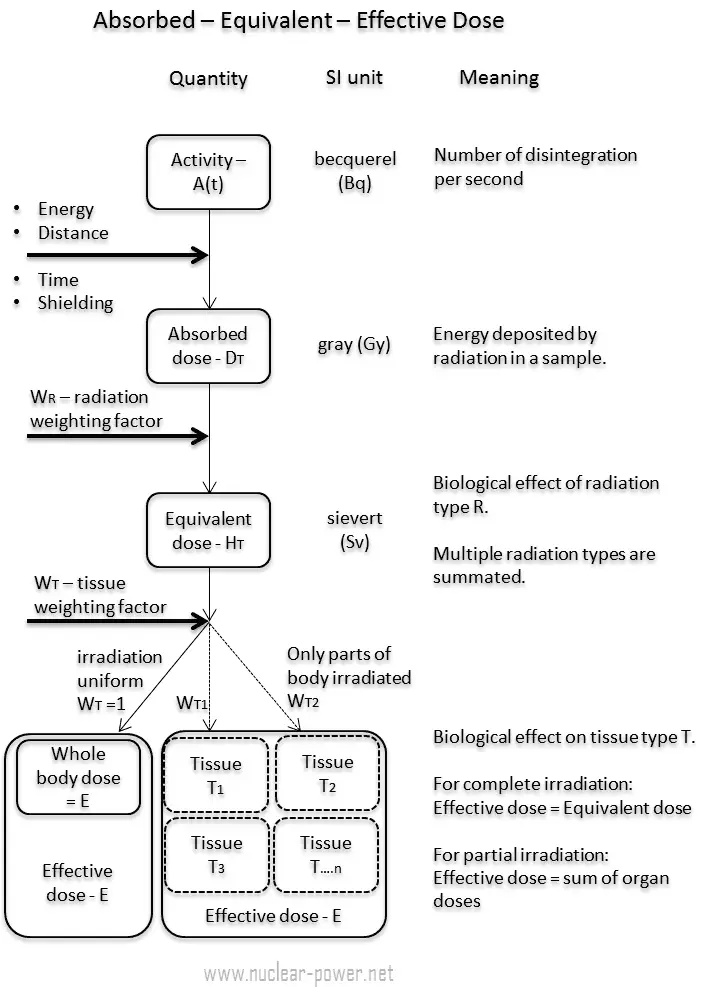
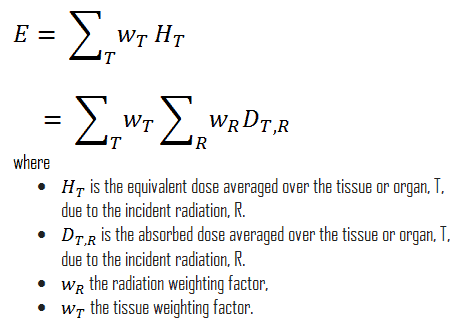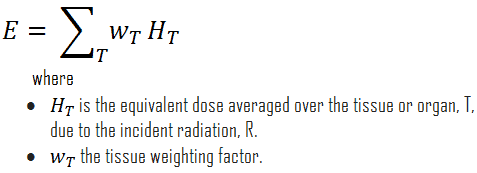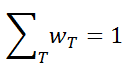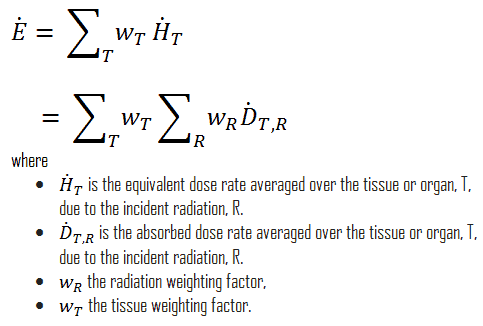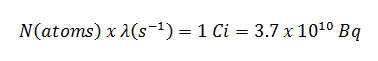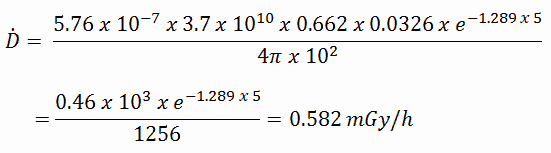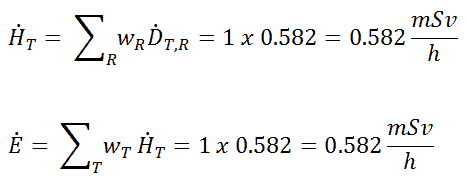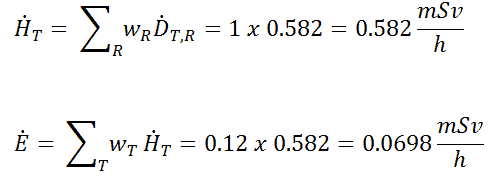In radiation protection, the effective dose is a dose quantity defined as the sum of the tissue-equivalent doses weighted by the ICRP organ (tissue) weighting factors, wT, which takes into account the varying sensitivity of different organs and tissues to radiation. Effective dose is given the symbol E. The SI unit of E is the sievert (Sv) or but rem (roentgen equivalent man) is still commonly used (1 Sv = 100 rem). Unit of sievert was named after the Swedish scientist Rolf Sievert, who did a lot of the early work on dosimetry in radiation therapy.
As was written in previous chapter, equivalent dose, HT, is used for assessing stochastic health risk due to external radiation fields that penetrate uniformly through the whole body. However it needs further corrections when the field is applied only to part(s) of the body, or non-uniformly to measure the overall stochastic health risk to the body. To enable this a further dose quantity called effective dose must be used. Effective dose allows to determine the biological consequences of partial irradiation (non-uniform). It is due to the fact, various body tissues react to ionising radiation in different ways. Therefore the ICRP has assigned sensitivity factors to specified tissues and organs so that the effect of partial irradiation can be calculated if the irradiated regions are known.
In Publication 60, the ICRP defined the effective dose as the doubly weighted sum of absorbed dose in all the organs and tissues of the body. Dose limits are set in terms of effective dose and apply to the individual for radiological protection purposes, including the assessment of risk in general terms. Mathematically, the effective dose can be expressed as:
Both equivalent dose and effective dose are quantities for use in radiological protection, including the assessment of risks in general terms. They provide a basis for estimating the probability of stochastic effects only for absorbed doses well below the thresholds for deterministic effects.
Units of effective dose:
- Sievert. The sievert is a derived unit of equivalent dose and effective dose and for represents the equivalent biological effect of the deposit of a joule of gamma rays energy in a kilogram of human tissue.
- REM. The rem (an abbreviation for Roentgen Equivalent Man) is the non-SI unit of equivalent dose and effective dose dose, which is used predominantly in the USA. It is a term for dose equivalence and equals the biological damage that would be caused by one rad of dose.
One sievert is a large amount of effective dose. A person who has absorbed a whole body dose of 1 Sv has absorbed one joule of energy in each kg of body tissue (in case of gamma rays).
Effective doses in industry and medicine often have usually lower doses than one sievert, and the following multiples are often used:
1 mSv (millisievert) = 1E-3 Sv
1 µSv (microsievert) = 1E-6 Sv
Conversions from the SI units to other units are as follows:
- 1 Sv = 100 rem
- 1 mSv = 100 mrem
Tissue Weighting Factors
The tissue weighting factor, wT, is the factor by which the equivalent dose in a tissue or organ T is weighted to represent the relative contribution of that tissue or organ to the total health detriment resulting from uniform irradiation of the body (ICRP 1991b). It represents a measure of the risk of stochastic effects that might result from exposure of that specific tissue. The tissue weighting factors take into account the varying sensitivity of different organs and tissues to radiation.
The tissue weighting factors are listed in various ICRP (International Commission on Radiological Protection) publications. According to the actual determination of the ICRP the risk factors are in the following table (from ICRP publication 103 (ICRP 2007)).
Special Reference: ICRP, 2007. The 2007 Recommendations of the International Commission on Radiological Protection. ICRP Publication 103. Ann. ICRP 37 (2-4).
For this purpose, the body has been divided into 15 different organs – each with a weighting factor wT. If only part of the body is irradiated, then only those regions are used to calculate the effective dose. The tissue weighting factors summate to 1.0, so that if an entire body is radiated with uniformly penetrating external radiation, the effective dose for the entire body is equal to the equivalent dose for the entire body.
If a person is irradiated only partially, the dose will depend strongly on the tissue, which was irradiated. For example, a 10 mSv gamma dose to the whole body and a 50 mSv dose to the thyroid is the same, in terms of risk, as a whole-body dose of 10 + 0.04 x 50 = 12 mSv.
Examples of Doses in Sieverts
We must note that radiation is all around us. In, around, and above the world we live in. It is a natural energy force that surrounds us. It is a part of our natural world that has been here since the birth of our planet. In the following points we try to express enormous ranges of radiation exposure, which can be obtained from various sources.
- 0.05 µSv – Sleeping next to someone
- 0.09 µSv – Living within 30 miles of a nuclear power plant for a year
- 0.1 µSv – Eating one banana
- 0.3 µSv – Living within 50 miles of a coal power plant for a year
- 10 µSv – Average daily dose received from natural background
- 20 µSv – Chest X-ray
- 40 µSv – A 5-hour airplane flight
- 600 µSv – mammogram
- 1 000 µSv – Dose limit for individual members of the public, total effective dose per annum
- 3 650 µSv – Average yearly dose received from natural background
- 5 800 µSv – Chest CT scan
- 10 000 µSv – Average yearly dose received from natural background in Ramsar, Iran
- 20 000 µSv – single full-body CT scan
- 175 000 µSv – Annual dose from natural radiation on a monazite beach near Guarapari, Brazil.
- 5 000 000 µSv – Dose that kills a human with a 50% risk within 30 days (LD50/30), if the dose is received over a very short duration.
As can be seen, low-level doses are common for everyday life. The previous examples can help illustrate relative magnitudes. From biological consequences point of view, it is very important to distinguish between doses received over short and extended periods. An “acute dose” is one that occurs over a short and finite period of time, while a “chronic dose” is a dose that continues for an extended period of time so that it is better described by a dose rate. High doses tend to kill cells, while low doses tend to damage or change them. Low doses spread out over long periods of time don’t cause an immediate problem to any body organ. The effects of low doses of radiation occur at the level of the cell, and the results may not be observed for many years.
Effective Dose Rate
The effective dose rate is the rate at which an effective dose is received. It is a measure of radiation dose intensity (or strength). The effective dose rate is therefore defined as:
In conventional units, it is measured in mSv/sec, Sv/hr, mrem/sec or rem/hr. Since the amount of radiation exposure depends directly (linearly) on the time people spend near the source of radiation, the effective dose is equal to the strength of the radiation field (dose rate) multiplied by the length of time spent in that field. The example above indicates a person could expect to receive a dose of 25 millirems by staying in a 50 millirems/hour field for thirty minutes.
Calculation of Shielded Dose Rate
Assume the point isotropic source which contains 1.0 Ci of 137Cs, which has a half-life of 30.2 years. Note that the relationship between half-life and the amount of a radionuclide required to give an activity of one curie is shown below. This amount of material can be calculated using λ, which is the decay constant of certain nuclide:
About 94.6 percent decays by beta emission to a metastable nuclear isomer of barium: barium-137m. The main photon peak of Ba-137m is 662 keV. For this calculation, assume that all decays go through this channel.
Calculate the primary photon dose rate, in sieverts per hour (Sv.h-1), at the outer surface of a 5 cm thick lead shield. Then calculate the equivalent and effective dose rates for two cases.
- Assume that this external radiation field penetrates uniformly through the whole body. That means: Calculate the effective whole-body dose rate.
- Assume that this external radiation field penetrates only lungs and the other organs are completely shielded. That means: Calculate the effective dose rate.
Note that, primary photon dose rate neglects all secondary particles. Assume that the effective distance of the source from the dose point is 10 cm. We shall also assume that the dose point is soft tissue and it can reasonably be simulated by water and we use the mass energy absorption coefficient for water.
See also: Gamma Ray Attenuation
See also: Shielding of Gamma Rays
Solution:
The primary photon dose rate is attenuated exponentially, and the dose rate from primary photons, taking account of the shield, is given by:
As can be seen, we do not account for the buildup of secondary radiation. If secondary particles are produced or if the primary radiation changes its energy or direction, then the effective attenuation will be much less. This assumption generally underestimates the true dose rate, especially for thick shields and when the dose point is close to the shield surface, but this assumption simplifies all calculations. For this case the true dose rate (with the buildup of secondary radiation) will be more than two times higher.
To calculate the absorbed dose rate, we have to use in the formula:
- k = 5.76 x 10-7
- S = 3.7 x 1010 s-1
- E = 0.662 MeV
- μt/ρ = 0.0326 cm2/g (values are available at NIST)
- μ = 1.289 cm-1 (values are available at NIST)
- D = 5 cm
- r = 10 cm
Result:
The resulting absorbed dose rate in grays per hour is then:
1) Uniform irradiation
Since the radiation weighting factor for gamma rays is equal to one and we have assumed the uniform radiation field (the tissue weighting factor is also equal to unity), we can directly calculate the equivalent dose rate and the effective dose rate (E = HT) from the absorbed dose rate as:
2) Partial irradiation
In this case we assume a partial irradiation of lungs only. Thus, we have to use the tissue weighting factor, which is equal to wT = 0.12. The radiation weighting factor for gamma rays is equal to one. As a result, we can calculate the effective dose rate as:
Note that, if one part of the body (e.g.,the lungs) receives a radiation dose, it represents a risk for a particularly damaging effect (e.g., lung cancer). If the same dose is given to another organ it represents a different risk factor.
If we want to account for the buildup of secondary radiation, then we have to include the buildup factor. The extended formula for the dose rate is then:
——–
We hope, this article, Effective Dose, helps you. If so, give us a like in the sidebar. Main purpose of this website is to help the public to learn some interesting and important information about radiation and dosimeters.
