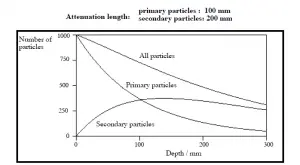
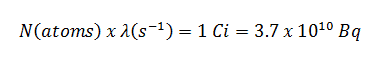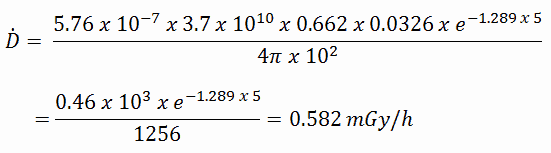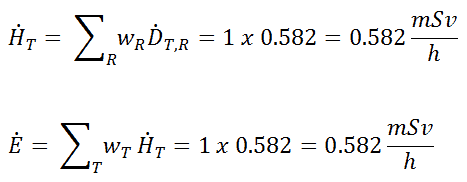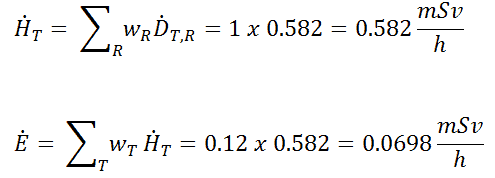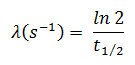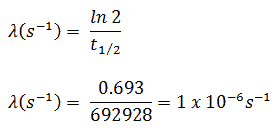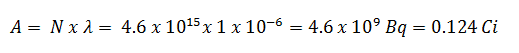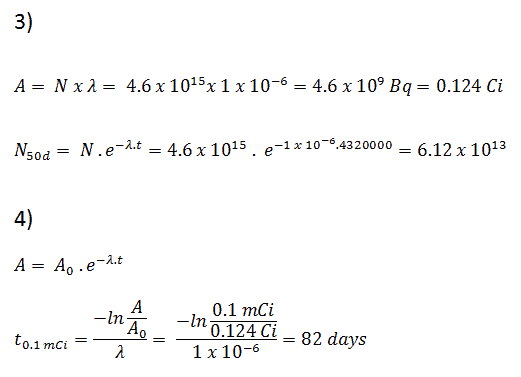- Limitando el tiempo. La cantidad de exposición a la radiación depende directamente (linealmente) del tiempo que las personas pasan cerca de la fuente de radiación. La dosis puede reducirse limitando el tiempo de exposición .
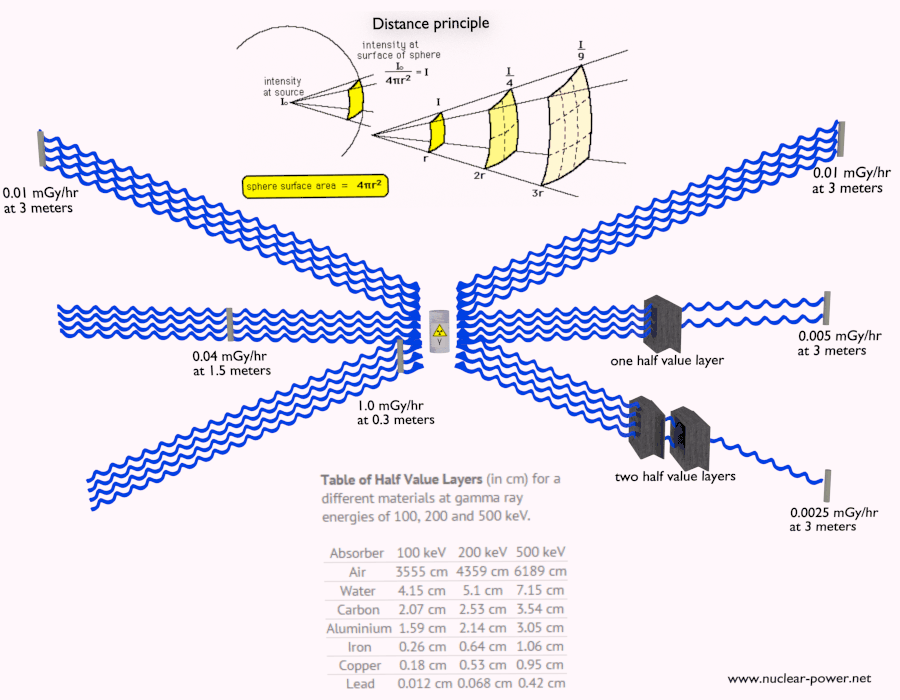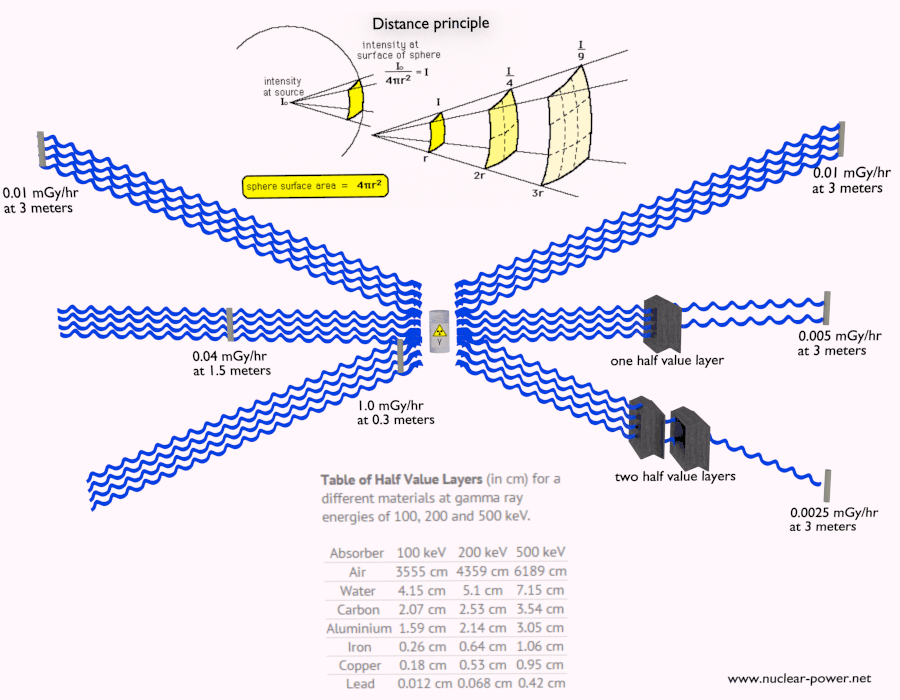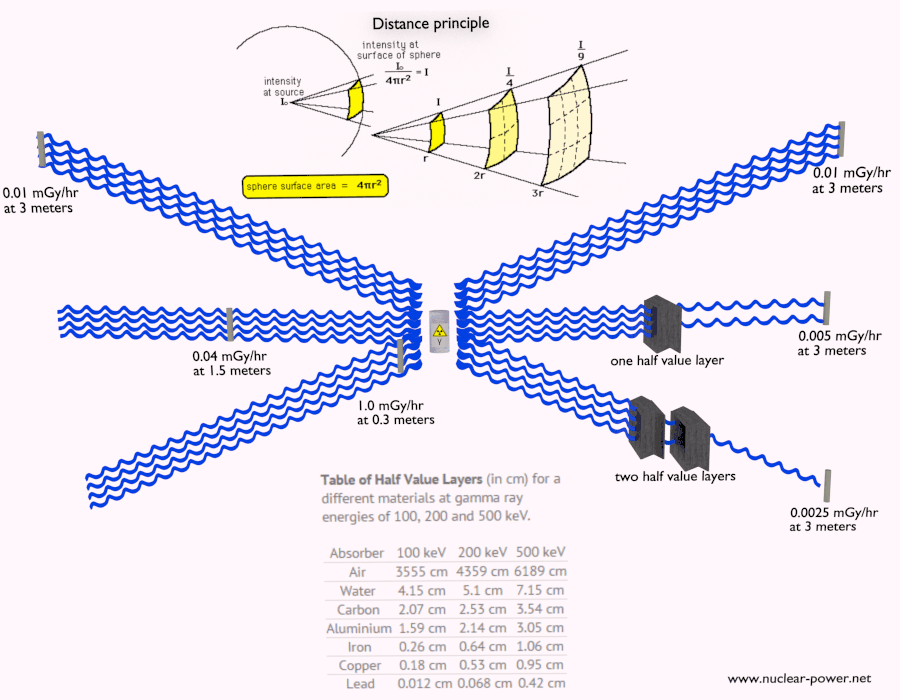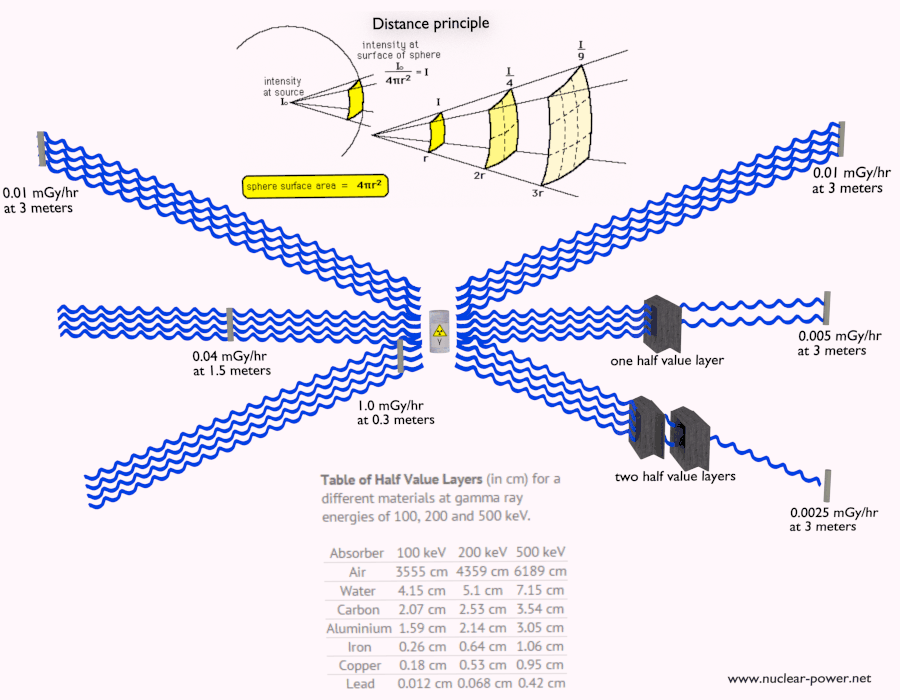
- Distancia. La cantidad de exposición a la radiación depende de la distancia desde la fuente de radiación. De manera similar al calor de un incendio, si está demasiado cerca, la intensidad de la radiación de calor es alta y puede quemarse. Si está a la distancia correcta, puede resistir allí sin ningún problema y, además, es cómodo. Si está demasiado lejos de la fuente de calor, la insuficiencia de calor también puede dañarlo. Esta analogía, en cierto sentido, puede aplicarse a la radiación también de fuentes de radiación.
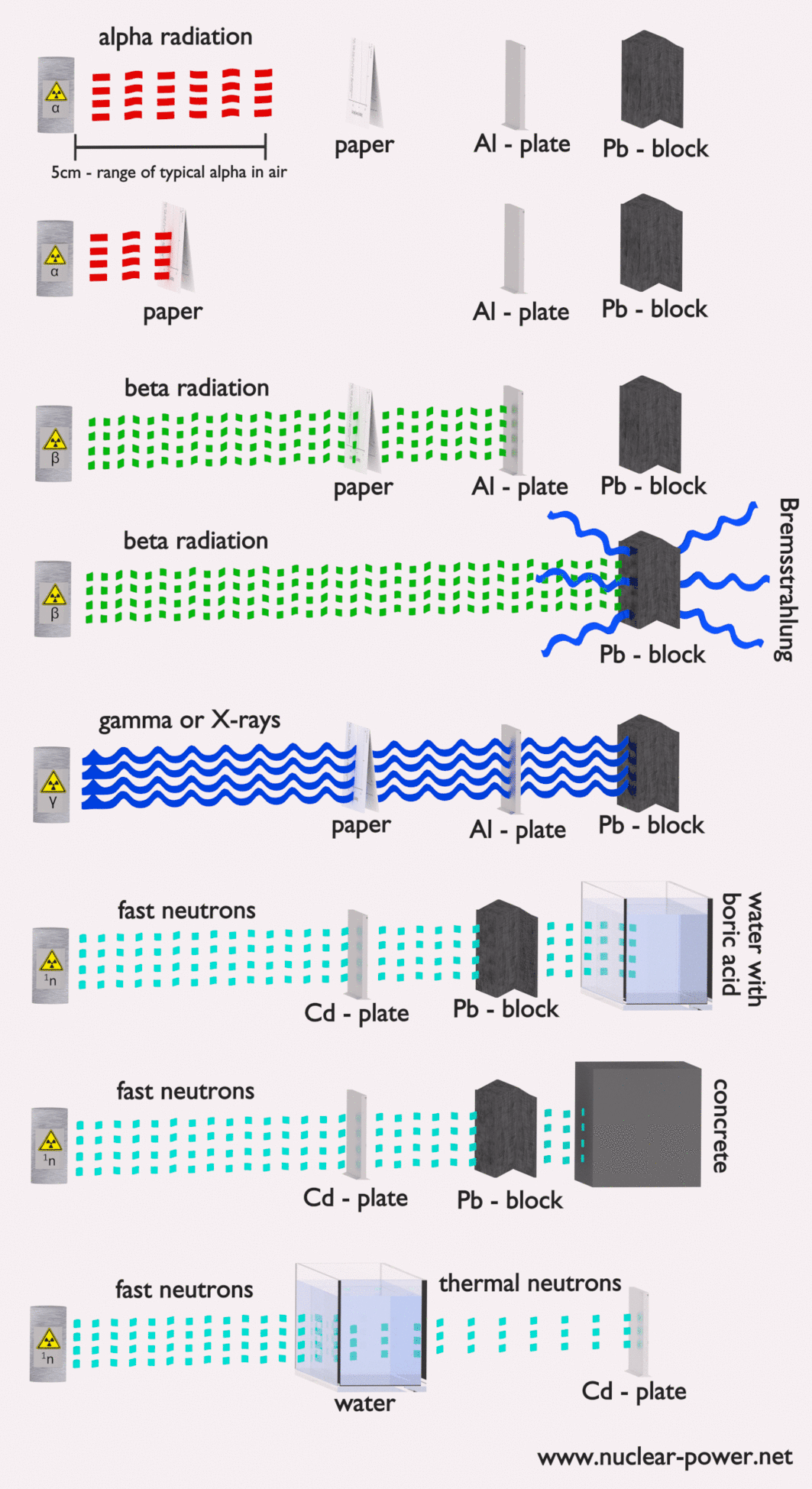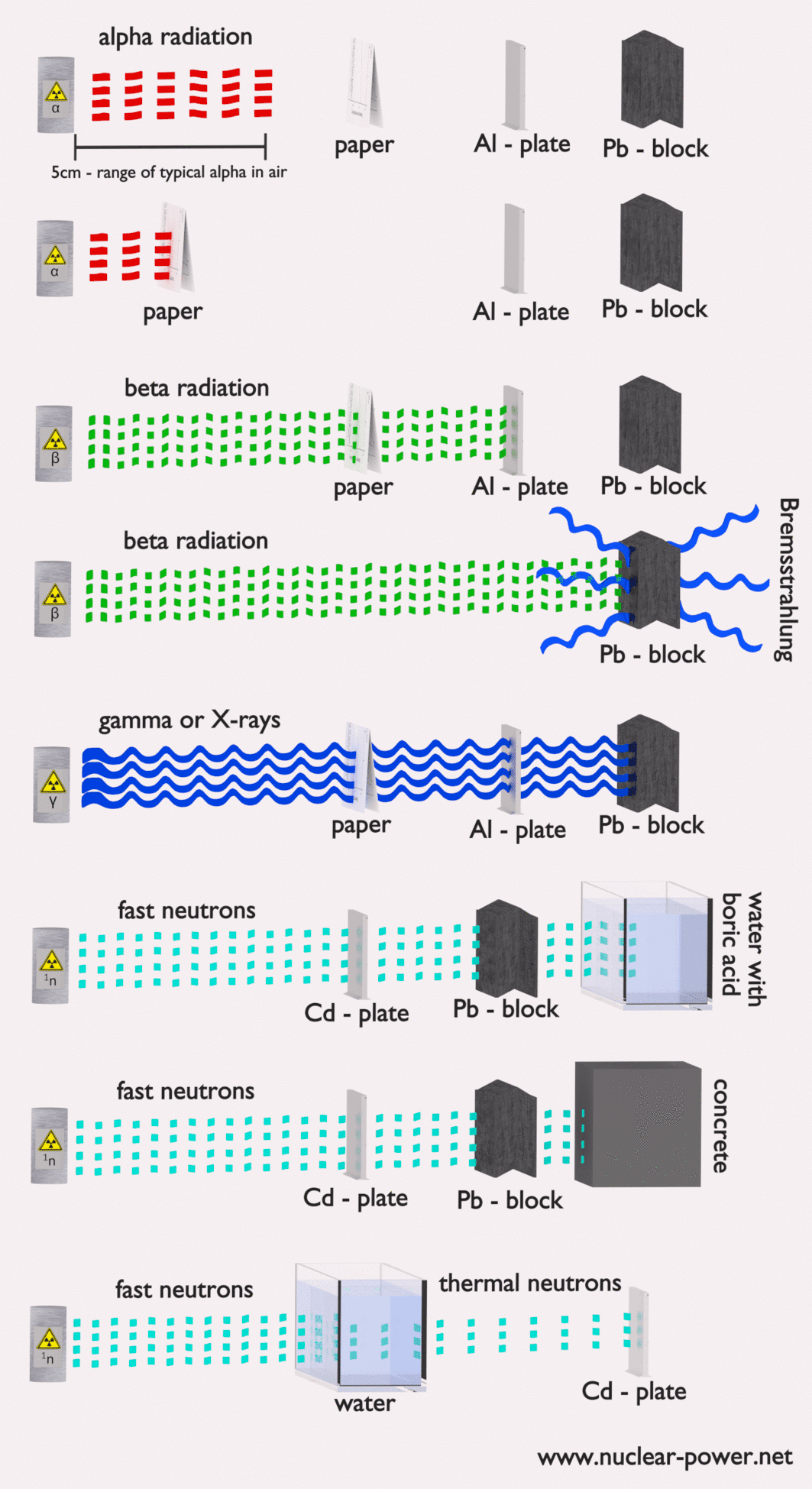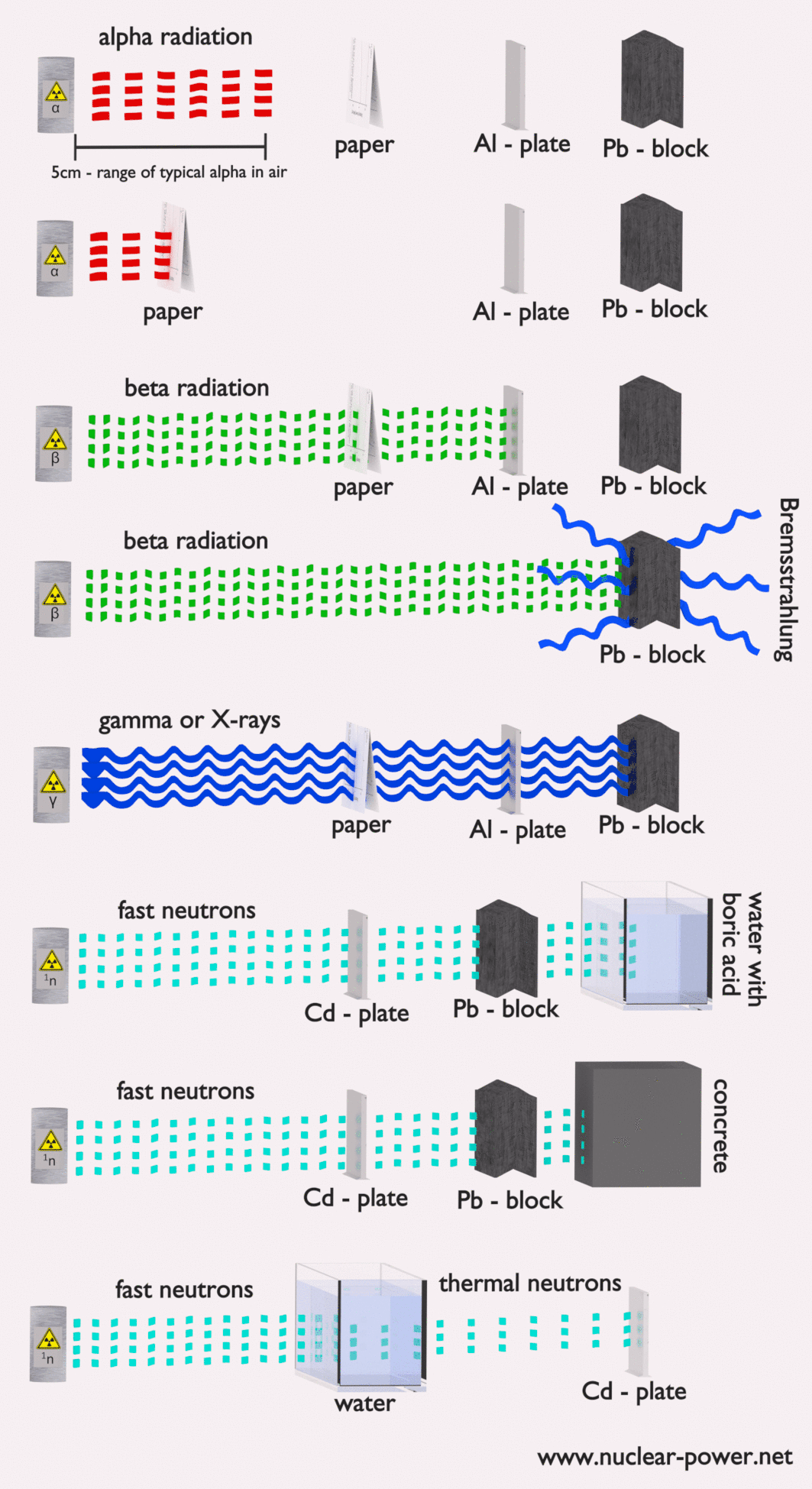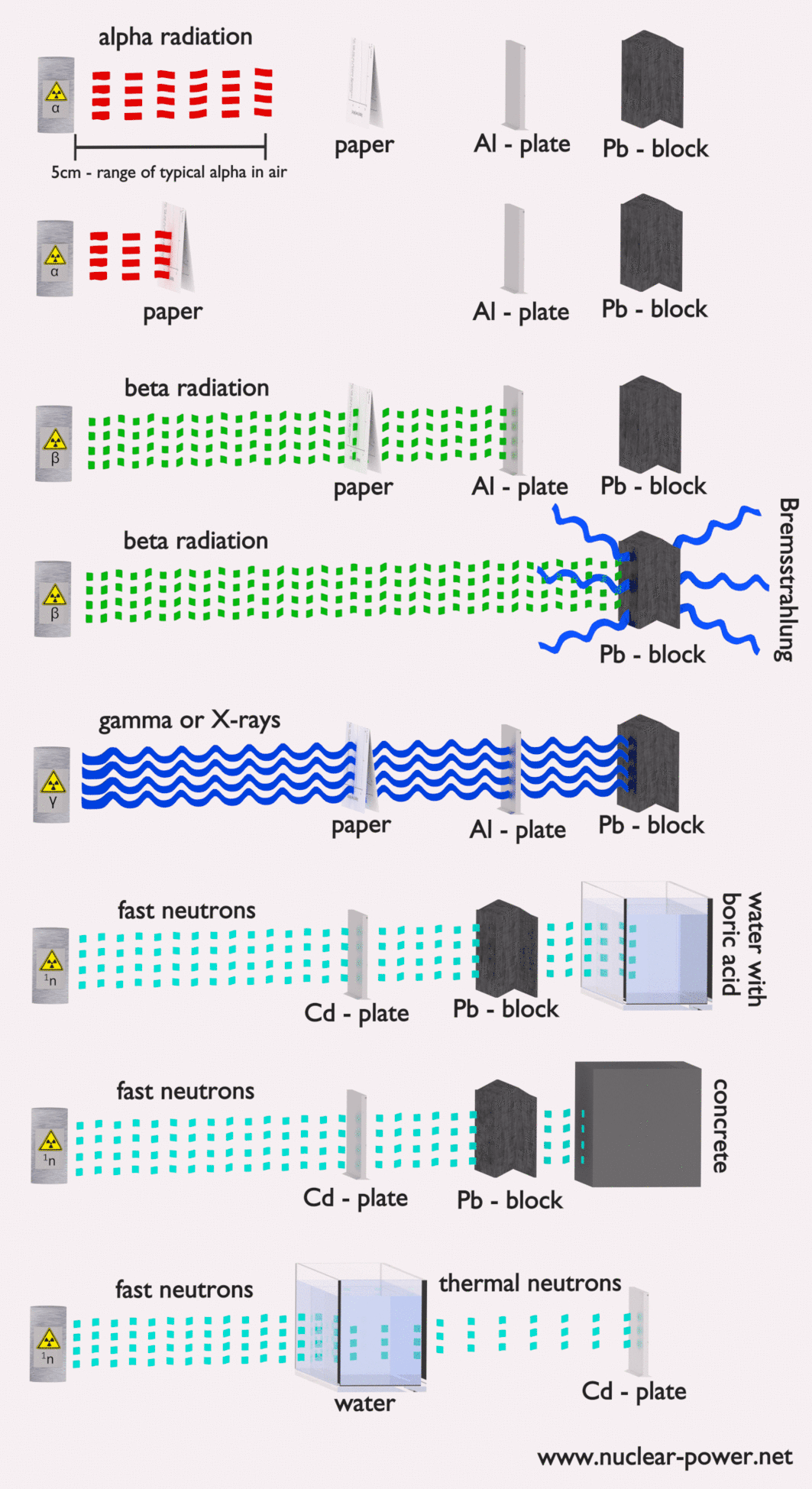
- Blindaje Finalmente, si la fuente es demasiado intensa y el tiempo o la distancia no proporcionan suficiente protección contra la radiación, se debe usar el blindaje. El blindaje contra la radiación generalmente consiste en barreras de plomo, concreto o agua. Hay muchos materiales que se pueden usar para proteger contra la radiación, pero hay muchas situaciones en la protección contra la radiación. Depende en gran medida del tipo de radiación que se va a proteger, su energía y muchos otros parámetros. Por ejemplo, incluso el uranio empobrecido puede usarse como una buena protección contra la radiación gamma, pero, por otro lado, el uranio es un blindaje absolutamente inapropiado de la radiación de neutrones .
- Tipo de radiación ionizante a proteger
- Espectro de energía de la radiación ionizante
- Duración de la exposición
- Distancia desde la fuente de la radiación ionizante
- Requisitos sobre la atenuación de la radiación ionizante: principios ALARA o ALARP
- Diseño grado de libertad
- Otros requisitos físicos (por ejemplo, transparencia en caso de pantallas de vidrio con plomo)
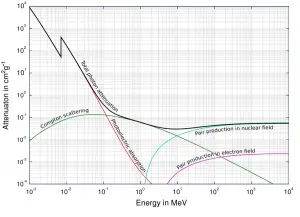
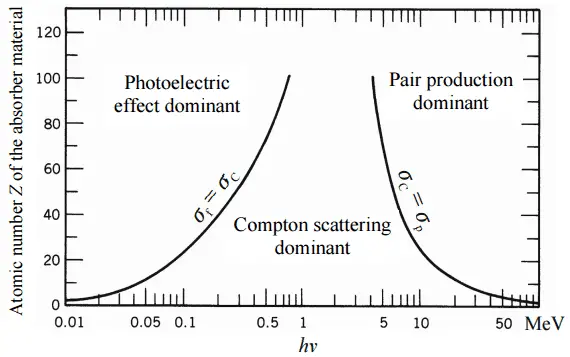
Ver también: interacción de la radiación con la materia
Ver también: Calculadora Rad Pro
Blindaje de la radiación en centrales nucleares
Generalmente en la industria nuclear, el blindaje contra la radiación tiene muchos propósitos. En las centrales nucleares, el objetivo principal es reducir la exposición a la radiación de personas y personal cerca de fuentes de radiación. En las centrales nucleares, la principal fuente de radiación es, de manera concluyente, el reactor nuclear y el núcleo del reactor . Los reactores nucleares se encuentran en general en potentes fuentes de espectro completo de tipos de radiación ionizante . El blindaje utilizado para este propósito se llama blindaje biológico .
Pero este no es el único propósito del blindaje contra la radiación. Los escudos también se usan en algunos reactores para reducir la intensidad de los rayos gamma o neutrones incidentes en el recipiente del reactor. Esta protección contra la radiación protege el recipiente del reactor y sus partes internas (por ejemplo, el cilindro de soporte del núcleo ) del calentamiento excesivo debido a la absorción de rayos gamma moderación rápida de neutrones . Tales escudos generalmente se denominan escudos térmicos .
Ver también: reflector de neutrones
Por lo general, se utiliza un poco de protección contra la radiación extraña para proteger el material del recipiente a presión del reactor (especialmente en las centrales eléctricas PWR ). Los materiales estructurales de los recipientes a presión y los componentes internos del reactor están dañados especialmente por neutrones rápidos . Los neutrones rápidos crean defectos estructurales, que en consecuencia conducen a la fragilidad del material del recipiente a presión . Para minimizar el flujo de neutrones en la pared del vaso, también se puede modificar la estrategia de carga del núcleo. En la estrategia de carga de combustible “hacia afuera”, se colocan nuevos conjuntos de combustible en la periferia del núcleo. Esta configuración provoca una alta fluencia de neutrones en la pared del vaso. Por lo tanto, la estrategia de carga de combustible «dentro-fuera» (con patrones de carga de baja fuga – L3P) se ha adoptado en muchas centrales nucleares. A diferencia de la estrategia de «entrada y salida», los núcleos de baja fuga tienen conjuntos de combustible nuevo en la segunda fila, no en la periferia del núcleo. La periferia contiene combustible con mayor consumo de combustible y menor potencia relativa y sirve como un escudo de radiación muy sofisticado.
En las centrales nucleares, el problema central es protegerse contra los rayos gamma y los neutrones , porque los rangos de partículas cargadas (como las partículas beta y las partículas alfa) en la materia son muy cortos. Por otro lado, debemos ocuparnos del blindaje de todos los tipos de radiación, porque cada reactor nuclear es una fuente importante de todos los tipos de radiación ionizante.
Cálculo de la tasa de dosis blindada en Sieverts de la superficie contaminada
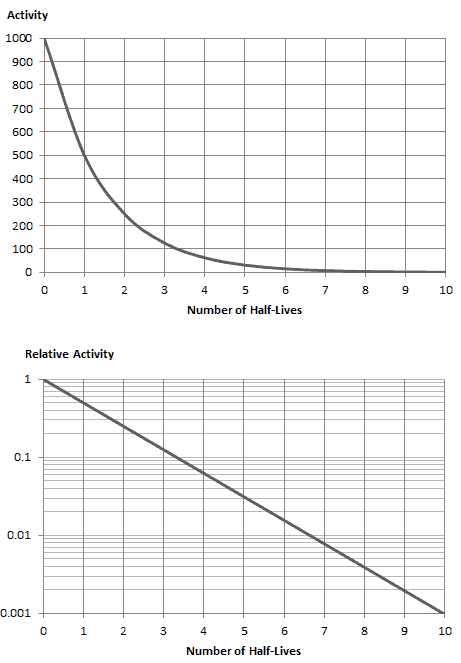
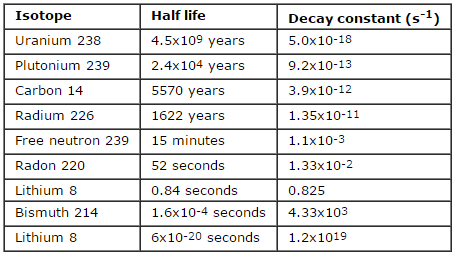
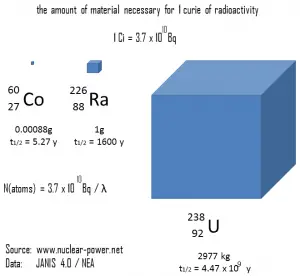
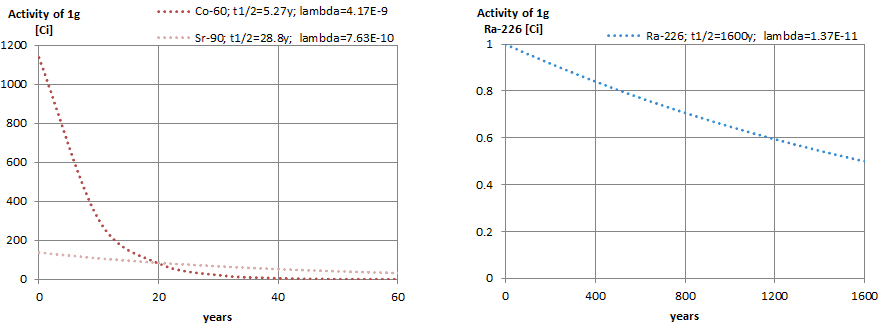
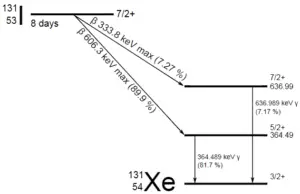
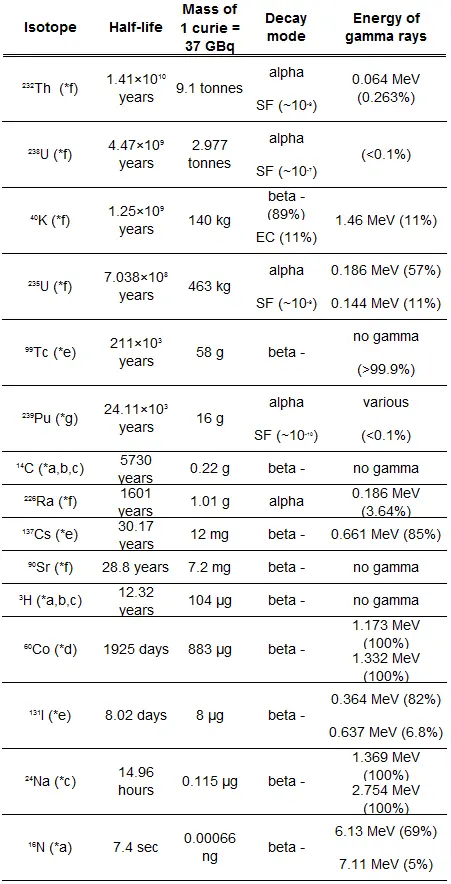
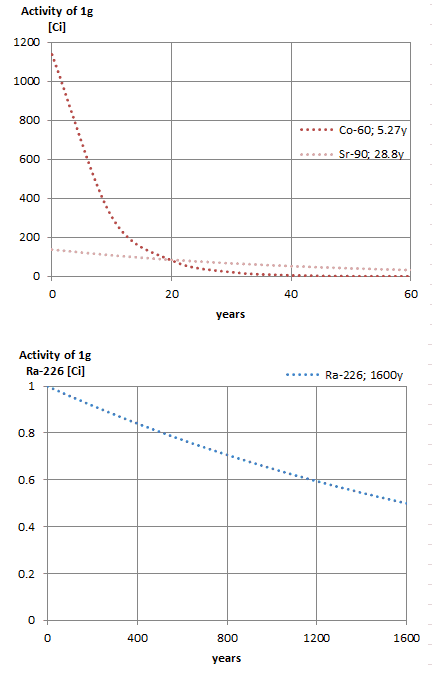
Suponga una superficie que está contaminada por 1.0 Ci de 137 Cs . Suponga que este contaminante puede ser aproximado por la fuente isotrópica puntual que contiene 1.0 Ci de 137 Cs , que tiene una vida media de 30.2 años . Tenga en cuenta que a continuación se muestra la relación entre la vida media y la cantidad de radionúclido requerida para dar una actividad de un curie . Esta cantidad de material se puede calcular usando λ, que es la constante de descomposición de ciertos nucleidos:
Alrededor del 94,6 por ciento se desintegra por emisión beta a un isómero nuclear de bario metaestable : bario-137m. El pico principal de fotones de Ba-137m es 662 keV . Para este cálculo, suponga que todas las desintegraciones pasan por este canal.
Calcule la tasa de dosis primaria de fotones , en sieverts por hora (Sv.h -1 ), en la superficie externa de un blindaje de plomo de 5 cm de espesor. Luego calcule las tasas de dosis equivalentes y efectivas para dos casos.
- Suponga que este campo de radiación externo penetra de manera uniforme en todo el cuerpo. Eso significa: Calcular la tasa de dosis efectiva de todo el cuerpo .
- Suponga que este campo de radiación externo penetra solo en los pulmones y los otros órganos están completamente protegidos. Eso significa: calcular la tasa de dosis efectiva .
Tenga en cuenta que, la tasa de dosis de fotones primarios descuida todas las partículas secundarias. Suponga que la distancia efectiva de la fuente desde el punto de dosis es de 10 cm . También supondremos que el punto de dosis es tejido blando y que puede ser simulado razonablemente por el agua y usamos el coeficiente de absorción de energía de masa para el agua.
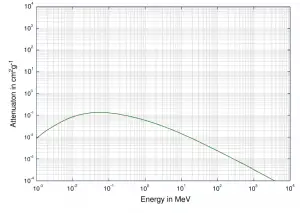
Ver también: atenuación de rayos gamma
Ver también: Blindaje de rayos gamma
Solución:
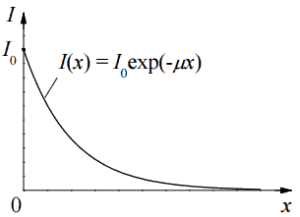
La tasa de dosis de fotones primarios se atenúa exponencialmente , y la tasa de dosis de fotones primarios, teniendo en cuenta el escudo, viene dada por:
Como se puede ver, no tenemos en cuenta la acumulación de radiación secundaria. Si se producen partículas secundarias o si la radiación primaria cambia su energía o dirección, entonces la atenuación efectiva será mucho menor. Esta suposición generalmente subestima la tasa de dosis real, especialmente para protecciones gruesas y cuando el punto de dosis está cerca de la superficie de la protección, pero esta suposición simplifica todos los cálculos. Para este caso, la tasa de dosis real (con la acumulación de radiación secundaria) será más de dos veces mayor.
Para calcular la tasa de dosis absorbida , tenemos que usar en la fórmula:
- k = 5,76 x 10 -7
- S = 3.7 x 10 10 s -1
- E = 0.662 MeV
- μ t / ρ = 0.0326 cm 2 / g (los valores están disponibles en NIST)
- μ = 1.289 cm -1 (los valores están disponibles en NIST)
- D = 5 cm
- r = 10 cm
Resultado:
La tasa de dosis absorbida resultante en grises por hora es entonces:
1) irradiación uniforme
Dado que el factor de ponderación de la radiación para los rayos gamma es igual a uno y hemos asumido el campo de radiación uniforme (el factor de ponderación del tejido también es igual a la unidad), podemos calcular directamente la tasa de dosis equivalente y la tasa de dosis efectiva (E = H T ) de la tasa de dosis absorbida como:
2) irradiación parcial
En este caso, suponemos una irradiación parcial de los pulmones solamente. Por lo tanto, tenemos que usar el factor de ponderación del tejido , que es igual a w T = 0.12 . El factor de ponderación de la radiación para los rayos gamma es igual a uno. Como resultado, podemos calcular la tasa de dosis efectiva como:
Tenga en cuenta que, si una parte del cuerpo (p. Ej., Los pulmones) recibe una dosis de radiación, representa un riesgo de un efecto particularmente perjudicial (p. Ej., Cáncer de pulmón). Si se administra la misma dosis a otro órgano, representa un factor de riesgo diferente.
Si queremos dar cuenta de la acumulación de radiación secundaria, entonces tenemos que incluir el factor de acumulación. La fórmula extendida para la tasa de dosis es entonces:
Factores de acumulación de blindaje contra rayos gamma
El factor de acumulación es un factor de corrección que considera la influencia de la radiación dispersa más cualquier partícula secundaria en el medio durante los cálculos de protección. Si queremos dar cuenta de la acumulación de radiación secundaria, entonces tenemos que incluir el factor de acumulación . El factor de acumulación es entonces un factor multiplicativo que da cuenta de la respuesta a los fotones no colidados para incluir la contribución de los fotones dispersos. Por lo tanto, el factor de acumulación se puede obtener como una relación de la dosis total a la respuesta para la dosis no contaminada.
La fórmula extendida para el cálculo de la tasa de dosis es:
El ANSI / ANS-6.4.3-1991 Coeficientes de atenuación de rayos gamma y factores de acumulación para el estándar de materiales de ingeniería, contiene coeficientes de atenuación de rayos gamma derivados y factores de acumulación para materiales y elementos de ingeniería seleccionados para usar en cálculos de blindaje (ANSI / ANS-6.1 .1, 1991).
……………………………………………………………………………………………………………………………….
Este artículo se basa en la traducción automática del artículo original en inglés. Para más información vea el artículo en inglés. Puedes ayudarnos. Si desea corregir la traducción, envíela a: [email protected] o complete el formulario de traducción en línea. Agradecemos su ayuda, actualizaremos la traducción lo antes posible. Gracias.