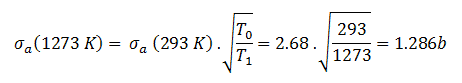Wechselwirkungen von Neutronen mit Materie
Neutronen sind neutrale Teilchen, deshalb bewegen sie sich in geraden Linien und weichen nur dann von ihrem Weg ab, wenn sie tatsächlich mit einem Kern kollidieren, um in eine neue Richtung gestreut oder absorbiert zu werden. Weder die Elektronen, die einen Kern umgeben (Atomelektronenwolke), noch das elektrische Feld, das durch einen positiv geladenen Kern verursacht wird, beeinflussen den Flug eines Neutrons. Kurz gesagt, Neutronen kollidieren mit Kernen , nicht mit Atomen. Ein sehr beschreibendes Merkmal der Transmission von Neutronen durch Schüttgut ist die mittlere freie Weglänge ( λ – Lambda ), dh die mittlere Entfernung, die ein Neutron zwischen Wechselwirkungen zurücklegt. Es kann aus folgender Gleichung berechnet werden:
λ = 1 / Σ
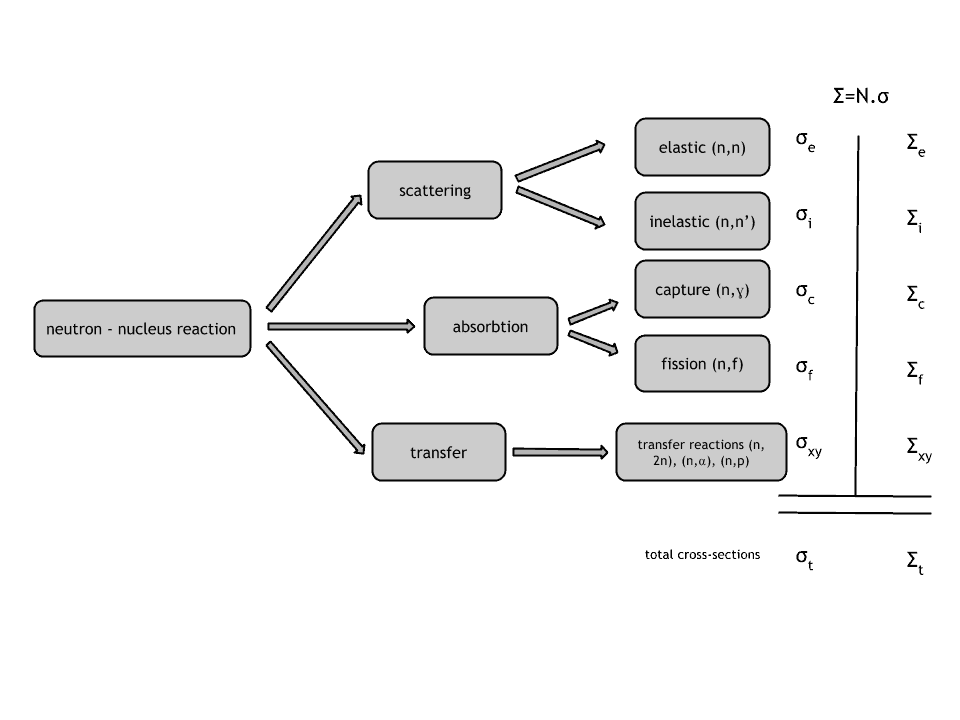
Neutronen können auf eine der folgenden Arten mit Kernen interagieren:
Arten von Neutronen-Kernreaktionen
Neutronenquerschnitt
Das Ausmaß, in dem Neutronen mit Kernen interagieren, wird anhand von Größen beschrieben, die als Querschnitte bekannt sind . Querschnitte werden verwendet, um die Wahrscheinlichkeit einer bestimmten Wechselwirkung zwischen einem einfallenden Neutron und einem Zielkern auszudrücken . Es ist zu beachten, dass diese Wahrscheinlichkeit nicht von den tatsächlichen Zieldimensionen abhängt. In Verbindung mit dem Neutronenfluss ermöglicht es die Berechnung der Reaktionsgeschwindigkeit, um beispielsweise die Wärmeleistung eines Kernkraftwerks abzuleiten. Die Standardeinheit zur Messung des mikroskopischen Querschnitts ( σ-Sigma ) ist der Stall , der 10 bis 28 m 2 entspricht. Diese Einheit ist sehr klein, daher werden üblicherweise Scheunen (abgekürzt als „b“) verwendet. Der mikroskopische Querschnitt kann als der effektive „Zielbereich“ interpretiert werden, in dem ein Kern mit einem einfallenden Neutron interagiert .
Ein makroskopischer Querschnitt ergibt sich aus dem Mikroskop und der Materialdichte:
Σ = σ.N.
Hier wird σ, das Einheiten von m 2 hat , als mikroskopischer Querschnitt bezeichnet. Da die Einheiten von N (Kerndichte) Kerne / m 3 sind , hat der makroskopische Querschnitt Σ Einheiten von m –1 , ist also tatsächlich ein falscher Name, da es sich nicht um eine korrekte Querschnittseinheit handelt.
Neutronenquerschnitte sind ein Schlüsselparameter für Kernbrennstoffe. Neutronenquerschnitte müssen für frische Brennelemente normalerweise in zweidimensionalen Modellen des Brenngitters berechnet werden.
Der Neutronenquerschnitt ist variabel und hängt ab von:
- Zielkern (Wasserstoff, Bor, Uran usw.) Jedes Isotop hat seine eigenen Querschnitte.
- Art der Reaktion (Einfang, Spaltung usw.). Die Querschnitte sind für jede Kernreaktion unterschiedlich.
- Neutronenenergie (thermisches Neutron, Resonanzneutron, schnelles Neutron). Für ein bestimmtes Ziel und einen bestimmten Reaktionstyp hängt der Querschnitt stark von der Neutronenenergie ab. Im allgemeinen Fall ist der Querschnitt bei niedrigen Energien gewöhnlich viel größer als bei hohen Energien. Aus diesem Grund verwenden die meisten Kernreaktoren einen Neutronenmoderator, um die Energie des Neutrons zu reduzieren und damit die Wahrscheinlichkeit der Spaltung zu erhöhen, die für die Energieerzeugung und die Aufrechterhaltung der Kettenreaktion unerlässlich ist.
- Zielenergie (Temperatur des Zielmaterials – Doppler-Verbreiterung) Diese Abhängigkeit ist nicht so signifikant, aber die Zielenergie beeinflusst die inhärente Sicherheit von Kernreaktoren aufgrund einer Doppler-Verbreiterung der Resonanzen stark.
Siehe auch: JANIS (Java-basierte Nuklearinformationssoftware)
Siehe auch: Neutronenquerschnitt
Gesetz 1 / v
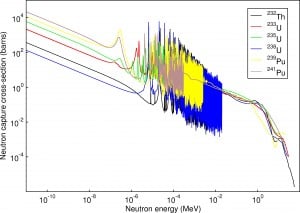
Quelle: JANIS 4.0
Bei thermischen Neutronen ( im 1 / v-Bereich ) nehmen die Absorptionsquerschnitte mit abnehmender Geschwindigkeit (kinetische Energie) des Neutrons zu. Daher kann das 1 / v-Gesetz verwendet werden, um die Verschiebung des Absorptionsquerschnitts zu bestimmen, wenn sich das Neutron im Gleichgewicht mit einem umgebenden Medium befindet. Dieses Phänomen ist darauf zurückzuführen, dass die Kernkraft zwischen dem Zielkern und dem Neutron eine längere Zeit zur Wechselwirkung hat.
Dieses Gesetz ist nur für den Absorptionsquerschnitt und nur im 1 / v-Bereich anwendbar.
Beispiel für Querschnitte im 1 / v-Bereich:
Der Absorptionsquerschnitt für 238U bei 20 ° C = 293 K (~ 0,0253 eV) beträgt:
.
Der Absorptionsquerschnitt für 238U bei 1000 ° C = 1273 K ist gleich:
Diese Querschnittsverringerung wird nur aufgrund der Temperaturverschiebung des umgebenden Mediums verursacht.
Resonanz-Neutroneneinfang
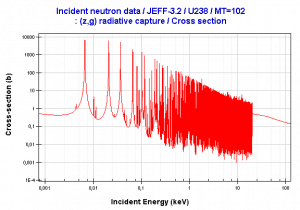
Quelle: JANIS-Programm
Der Absorptionsquerschnitt hängt häufig stark von der Neutronenenergie ab. Beachten Sie, dass die Kernspaltung Neutronen mit einer mittleren Energie von 2 MeV (200 TJ / kg, dh 20.000 km / s) erzeugt. Das Neutron kann grob in drei Energiebereiche unterteilt werden:
- Schnelles Neutron. (10 MeV – 1 keV)
- Resonanzneutron (1keV – 1eV)
- Thermisches Neutron. (1 eV – 0,025 eV)
Die Resonanzneutronen werden wegen ihres besonderen Verhaltens als Resonanz bezeichnet. Bei Resonanzenergien kann der Querschnitt Spitzen erreichen, die mehr als 100x höher sind als der Basiswert des Querschnitts. Bei diesen Energien übersteigt der Neutroneneinfang die Spaltwahrscheinlichkeit erheblich. Daher ist es (für thermische Reaktoren) sehr wichtig , diesen Energiebereich schnell zu überwinden und den Reaktor mit thermischen Neutronen zu betreiben, was zu einer Erhöhung der Spaltwahrscheinlichkeit führt.
Doppler-Verbreiterung
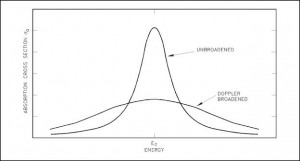
Eine Doppler-Verbreiterung der Resonanzen ist ein sehr wichtiges Phänomen, das die Reaktorstabilität verbessert . Der sofortige Temperaturkoeffizient der meisten thermischen Reaktoren ist aufgrund eines nuklearen Doppler-Effekts negativ . Obwohl der Absorptionsquerschnitt wesentlich von der einfallenden Neutronenenergie abhängt, hängt die Form der Querschnittskurve auch von der Zieltemperatur ab.
Kerne befinden sich in Atomen, die sich aufgrund ihrer Wärmeenergie selbst ständig bewegen . Infolge dieser thermischen Bewegungen scheinen Neutronen, die auf ein Ziel treffen, den Kernen im Ziel eine kontinuierliche Energieverteilung zu haben. Dies wirkt sich wiederum auf die beobachtete Resonanzform aus. Die Resonanz wird kürzer und breiter als in Ruhe der Kerne.
Obwohl sich die Form einer Resonanz mit der Temperatur ändert, bleibt die Gesamtfläche unter der Resonanz im Wesentlichen konstant. Dies bedeutet jedoch keine konstante Neutronenabsorption . Trotz der konstanten Resonanzfläche nimmt ein Resonanzintegral , das die Absorption bestimmt, mit zunehmender Zieltemperatur zu. Dies verringert natürlich den Koeffizienten k (negative Reaktivität wird eingefügt).
Typische Materialquerschnitte im Reaktor
Die folgende Tabelle zeigt die Neutronenquerschnitte der häufigsten Isotope des Reaktorkerns.
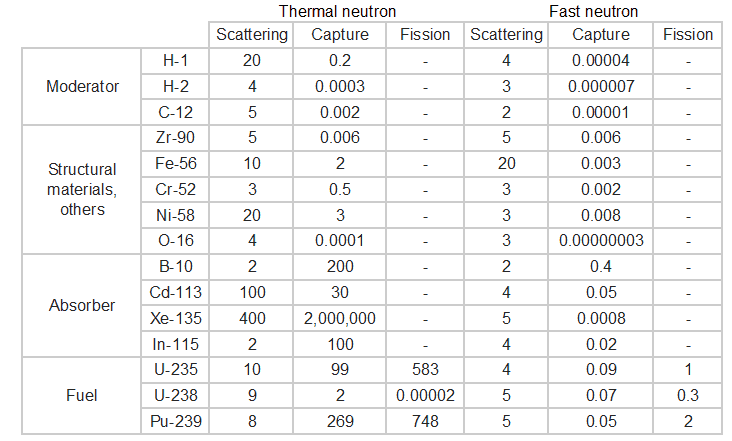
……………………………………………………………………………………………………………………………….
Dieser Artikel basiert auf der maschinellen Übersetzung des englischen Originalartikels. Weitere Informationen finden Sie im Artikel auf Englisch. Sie können uns helfen. Wenn Sie die Übersetzung korrigieren möchten, senden Sie diese bitte an: [email protected] oder füllen Sie das Online-Übersetzungsformular aus. Wir bedanken uns für Ihre Hilfe und werden die Übersetzung so schnell wie möglich aktualisieren. Danke.