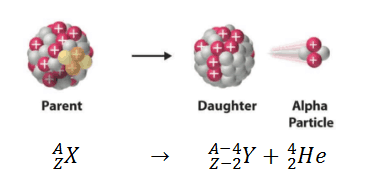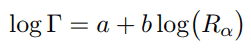Was ist die Theorie des Alpha-Zerfalls – Quantentunneln – Definition

Theorie des Alpha-Zerfalls – Quantentunneln

Alpha-Zerfall  (oder α-Zerfall und auch Alpha-Radioaktivität ) bezeichnet den Zerfall eines Elternkerns zu einer Tochter durch die Emission des Kerns eines Heliumatoms. Dieser Übergang kann charakterisiert werden als:

Wie aus der Abbildung ersichtlich ist, werden Alpha-Partikel beim Alpha-Zerfall emittiert.

Unter der Vielzahl von Kanälen, in denen ein Kern zerfällt, war der Alpha-Zerfall einer der am meisten untersuchten. Der Alpha-Zerfallskanal in schweren und superschweren Kernen lieferte Informationen über die grundlegenden Eigenschaften von Kernen, die weit von der Stabilität entfernt sind, wie z. B. ihre Grundzustandsenergien und die Struktur ihres Kernniveaus.

Der Alpha-Zerfall ist ein Quantentunnelungsprozess . Um emittiert zu werden, muss das Alpha-Teilchen eine Potentialbarriere durchdringen. Dies ähnelt dem Clusterzerfall , bei dem ein Atomkern einen kleinen „Cluster“ von Neutronen und Protonen (z . B. ¹² C) emittiert .

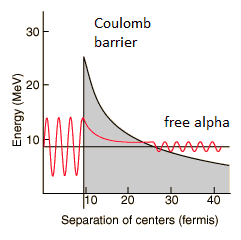
Die Höhe der Coulomb-Barriere für Kerne von A «200 beträgt etwa 20-25 MeV . Die beim Kernzerfall emittierten Alpha-Teilchen haben typische Energien von etwa 5 MeV. Einerseits wird ein ankommendes 5-MeV-Alpha-Teilchen von einem schweren Kern gestreut, und es kann die Coulomb-Barriere nicht durchdringen und kommt dem Kern so nahe, dass es durch die starke Kraft interagieren kann. Andererseits kann ein 5-MeV-Alpha-Teilchen, das in einem Kernpotentialtopf gebunden ist, dieselbe Coulomb-Barriere tunneln.

Bis 1928 hatte George Gamow (und unabhängig von Ronald Gurney und Edward Condon ) die Theorie des Alpha-Zerfalls durch Quantentunneln gelöst. Sie nahmen an, dass das Alpha-Teilchen und der Tochterkern vor seiner Dissoziation im Elternkern existieren, nämlich beim Zerfall der quasistationären Zustände (QS). Ein quasistationärer Zustand ist definiert als ein langlebiger Zustand, der schließlich zerfällt. Anfänglich oszilliert der Alpha-Cluster im Potential des Tochterkerns, wobei das Coulomb-Potential deren Trennung verhindert. Das Alpha-Teilchen wird vom Kern in einer Potentialwanne gefangen. Klassisch ist es verboten zu entkommen, aber nach den (damals) neu entdeckten Prinzipien der Quantenmechanik besteht eine winzige (aber nicht null) Wahrscheinlichkeit, dass es durch die Barriere „tunnelt“ und auf der anderen Seite erscheint, um dem Kern zu entkommen . Gamow, Condon und Gurney berechneten unter Verwendung des Tunnelmechanismus die Penetrierbarkeit des Tunnel-α-Partikels durch die Coulomb-Barriere. Ermittlung der Lebensdauern einiger α-emittierender Kerne. Der Haupterfolg dieses Modells war die Reproduktion des semi-empirischen Geiger-Nuttall-Gesetzes, das die Lebensdauern der α-Emitter in Bezug auf die Energien der freigesetzten α-Teilchen ausdrückt. Es ist zu beachten, dass andere übliche Zerfallsformen (z. B. Beta-Zerfall) durch das Zusammenspiel von Kernkraft und elektromagnetischer Kraft bestimmt werden.

Spezielle Referenz: WSC Williams. Kern- und Teilchenphysik. Clarendon Press; 1 edition, 1991, ISBN: 978-0198520467.

Geiger-Nuttall-Gesetz

Das Geiger-Nuttall-Gesetz ist ein semi-empirisches Gesetz, das die Lebensdauer (Halbwertszeit) des Alpha-Emitters in Form der Energie des freigesetzten Alpha-Teilchens ausdrückt. Mit anderen Worten heißt es, dass kurzlebige Isotope mehr energetische Alphateilchen emittieren als langlebige. Diese Regel wurde 1911 von Hans Geiger und John Mitchell Nuttall vor der Entwicklung der theoretischen Formulierung formuliert. Das Geiger-Nuttall-Gesetz kann mathematisch ausgedrückt werden als:

Dabei sind a und b empirische Konstanten, die sich aus logarithmischen Darstellungen experimenteller Daten ergeben. R _α stellt den linearen Bereich des Alphateilchens dar und ist somit ein direktes Maß für die kinetische Energie des Alphateilchens. Die Breite der Resonanz (Γ) ist im Allgemeinen mit der mittleren Lebensdauer (τ) des angeregten Kerns durch die Beziehung verbunden: Γ = ℏ / τ