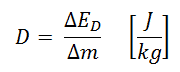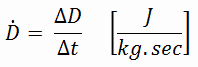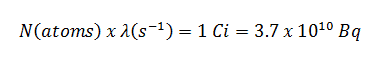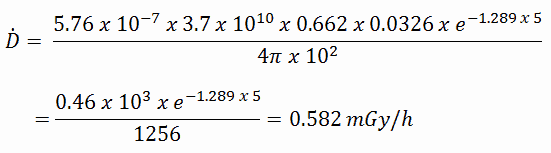Energiedosis – Gleichung
Die Energiedosis ist definiert als die Energiemenge, die durch ionisierende Strahlung in einer Substanz abgegeben wird. Energiedosis wird das Symbol gegeben D . Die Energiedosis wird normalerweise in einer Einheit gemessen, die als Gray (Gy) bezeichnet wird und vom SI-System abgeleitet ist. Gelegentlich wird auch sterben Nicht-SI-Einheit rad verwendet, überwiegend in den USA.
Einheiten der Energiedosis:
- Grau . Eine Dosis von einem Grau entspricht einer Energieeinheit (Joule), sterben in einem Kilogramm eines Stoffes gespeichert ist.
- RAD . Eine Dosis von einem Rad entspricht der Ablagerung von einhundert Erg Energie in einem Gramm eines beliebigen Materials.
Absorbierte Dosisleistung – Gleichung
Die Energiedosisrate ist die Rate, mit der eine Energiedosis empfangen WIRD. Es ist eine Maß für die Strahlungsdosisintensität (oder -stärke). Die Energiedosisleistung ist daher definiert als:
In Einheiten wird er in mrad/s , rad/h, mGy/s oder Gy/h bisher gemessen. Da sterben Höhe der Strahlenexposition direkt (linear) von der Zeit aus, sterben Menschen in der Nähe der Strahlungsquelle verbringen, sterben entspricht der reduzierten Dosis der Stärke des Strahlungsfeldes (Dosisleistung) multipliziert mit der Zeitdauer, sterben in diesem Feld verbracht wird. Das obige Beispiel zeigt, dass eine Person eine Dosis von 25 Millirems erwarten kann, wenn sie 30 Minuten lang in einem Feld von 50 Millirems / Stunde bleibt.
Absorbierte Dosisleistungsberechnung
Angenommen, die punktisotrope Quelle enthält 1,0 Ci von 137 Cs und hat eine Halbwertszeit von 30,2 Jahren . Es ist zu beachten, dass die Beziehung zwischen der Halbwertszeit und der Menge eines Radionuklids erforderlich ist, um eine Aktivität von Einem Curie zu ergeben . Diese Materialmenge kann mit λ berechnet werden, was die Zerfallskonstante eines bestimmten Nuklids ist:
Etwa 94,6 Prozent zerfallen durch Beta-Emission zu einem metastabilen Kernisomer von Barium: Barium-137m. Der Hauptphotonenpeak von Ba-137m beträgt 662 keV . Für this Berechnung WIRD angenommen, dass alle Zerfälle diesen Kanal durchlaufen.
Bestimmen Sie die primäre Photonendosisrate in Grau pro Stunde (Gy.h- 1 ) an der Außenfläche eines 5 cm dicken Bleischilds. Die Primärphotonendosisrate vernachlässigt alle Sekundärteilchen. Angenommen, der effektive Abstand der Quelle vom Dosispunkt beträgt 10 cm . Wir werden auch annehmen, dass der Dosispunkt Weichgewebe ist und vernünftigerweise durch Wasser simuliert Werden can, und wir verwenden den Massenenergieabsorptionskoeffizienten für Wasser.
Siehe auch: Gammastrahlendämpfung
Siehe auch: Abschirmung von Gammastrahlen
Lösung:
Die Primärphotonendosisrate WIRD exponentiell abgeschwächt , und sterben Dosisrate von Primärphotonen unter Berücksichtigung der Abschirmung ist gegeben durch:
Wie zu sehen ist, berücksichtigen wir den Aufbau von Sekundärstrahlung nicht. Wenn Sekundärteilchen erzeugt werden oder wenn sterben Primärstrahlung ihre Energie oder Richtung ändert, ist die effektive Dämpfung viel geringer. This Annahme unterschätzt im Allgemeinen sterben wahre Dosisleistung, insbesondere für dicke Schilde und WENN der Dosispunkt nahe an der Schildoberfläche liegt, aber this Annahme vereinfacht alle Berechnungen. In diesem Fall ist die tatsächliche Dosisleistung (mit dem Aufbau von Sekundärstrahlung) mehr als doppelt so hoch.
Um die übrige Dosisleistung zu berechnen , Wann müssen wir in der Formel Folgendes verwenden:
- k = 5,76 · 10 & supmin; & sup7;
- S = 3,7 × 10 10 s –1
- E = 0,662 MeV
- μ t / ρ = 0,0326 cm 2 / g (Werte sind bei NIST erhältlich)
- μ = 1,289 cm -1 (Werte sind beim NIST erhältlich)
- D = 5 cm
- r = 10 cm
Ergebnis:
Die resultierende Energiedosisleistung in Grays pro Stunde beträgt dann:
Wenn wir den Aufbau von Sekundärstrahlung berücksichtigen wollen, müssen wir den Aufbaufaktor einbeziehen. Die erweiterte Formel für die Dosisleistung lautet dann:
——–