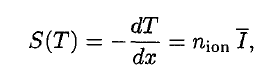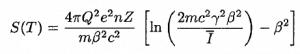Radiation Dosimetry

In radiation protection, the committed dose is a dose quantity that measures the stochastic health risk due to an intake of radioactive material into the human body. Commited dose is given the symbol E(t), where t is the integration time in years following the intake. The SI unit of E(t) is the sievert (Sv) or but rem (roentgen equivalent man) is still commonly used (1 Sv = 100 rem). Unit of sievert was named after the Swedish scientist Rolf Sievert, who did a lot of the early work on dosimetry in radiation therapy.

Committed dose allows to determine the biological consequences of irradiation caused by radioactive material, that  is inside our body. A committed dose of 1 Sv from an internal source represents the same effective risk as the same amount of effective dose of 1 Sv applied uniformly to the whole body from an external source.

As an example, let assume an intake of radioactive tritium. For tritium, the annual limit intake (ALI) is 1 x 10⁹ Bq. If you take in 1 x 10⁹ Bq of tritium, you will receive a whole-body dose of 20 mSv. Note that, the biological half-life about 10 days, while the radioactive half-life is about 12 years. Instead of years, it takes a couple of months until the tritium has been pretty well eliminated. The committed effective dose, E(t), is therefore 20 mSv. It does not depend whether a person intakes this amount of activity in a short time or in a long time. In every case, this person gets the same whole-body dose of 20 mSv.

The ICRP defines two dose quantities for individual committed dose.

Committed Effective Dose

According to the ICRP, the committed effective dose, E(t) is defined as:

“The sum of the products of the committed organ or tissue equivalent doses and the appropriate tissue weighting factors (w_T), where t is the integration time in years following the intake. The commitment period is taken to be 50 years for adults, and to age 70 years for children.”

Committed Equivalent Dose

According to the ICRP, the committed equivalent dose, H_T(t) is defined as:

“The time integral of the equivalent dose rate in a particular tissue or organ that will be received by an individual following intake of radioactive material into the body by a Reference Person, where t is the integration time in years.”

Special Reference: ICRP, 2007. The 2007 Recommendations of the International Commission on Radiological Protection. ICRP Publication 103. Ann. ICRP 37 (2-4).

Internal Dose Uptake

If the source of radiation is inside our body, we say, it is internal exposure. The intake of radioactive material can occur through various pathways such as ingestion of radioactive contamination in food or liquids, inhalation of radioactive gases, or through intact or wounded skin. Most radionuclides will give you much more radiation dose if they can somehow enter your body, than they would if they remained outside.

But when a radioactive compound enters the body, the activity will decrease with time, due both to radioactive decay and to biological clearance. The decrease varies from one radioactive compound to another. For this purpose, the biological half-life is defined in radiation protection.

The biological half-life is the time taken for the amount of a particular element in the body to decrease to half of its initial value due to elimination by biological processes alone, when the rate of removal is roughly exponential. The biological half-life depends on the rate at which the body normally uses a particular compound of an element. Radioactive isotopes that were ingested or taken in through other pathways will gradually be removed from the body via bowels, kidneys, respiration and perspiration. This means that a radioactive substance can be expelled before it has had the chance to decay.

As a result, the biological half-life significantly influences the effective half-life and the overall dose from internal contamination. If a radioactive compound with radioactive half-life (t_1/2) is cleared from the body with a biological half-life t_b, the effective half-life (t_e) is given by the expression:

As can be seen, the biological mechanisms always decreases the overall dose from internal contamination.  Moreover, if t_1/2 is large in comparison to t_b, the effective half-life is approximately the same as t_b.

For example, tritium has the biological half-life about 10 days, while the radioactive half-life is about 12 years. On the other hand, radionuclides with very short radioactive half-lives have also very short effective half-lives. These radionuclides will deliver, for all practical purposes, the total radiation dose within the first few days or weeks after intake.

For tritium, the annual limit intake (ALI) is 1 x 10⁹ Bq. If you take in 1 x 10⁹ Bq of tritium, you will receive a whole-body dose of 20 mSv. The committed effective dose, E(t), is therefore 20 mSv. It does not depend whether a person intakes this amount of activity in a short time or in a long time. In every case, this person gets the same whole-body dose of 20 mSv.

See also:

Effective Dose

See above:See also:

Gamma Ray  

See also:

Discovery of Gamma Rays

Characteristics of Gamma Rays / Radiation

• Gamma rays are high-energy photons (about 10 000 times as much energy as the visible photons),
• The same photons as the photons forming the visible range of the electromagnetic spectrum – light.
• Photons (gamma rays and X-rays) can ionize atoms directly (despite they are electrically neutral) through the Photoelectric effect and the Compton effect, but secondary (indirect) ionization is much more significant.
• Gamma rays ionize matter primarily via indirect ionization.
• Although a large number of possible interactions are known, there are three key interaction mechanisms  with matter.
  • Photoelectric effect
  • Compton scattering
  • Pair production
• Gamma rays travel at the speed of light and they can travel thousands of meters in air before spending their energy.
• Since the gamma radiation is very penetrating matter, it must be shielded by very dense materials, such as lead or uranium.
• The distinction between X-rays and gamma rays is not so simple and has changed in recent decades.  According to the currently valid definition, X-rays are emitted by electrons outside the nucleus, while gamma rays are emitted by the nucleus.
• Gamma rays frequently accompany the emission of alpha and beta radiation.

See also:

Discovery of Gamma Rays

See also:

Gamma Ray

See also:

Photoelectric Effect

Description of Gamma Radiation

Gamma rays, also known as gamma radiation, refers to electromagnetic radiation (no rest mass, no charge) of a very high energies. Gamma rays are high-energy photons with very short wavelengths and thus very high frequency. Since the gamma rays are in substance only a very high-energy photons, they are very penetrating matter and are thus biologically hazardous. Gamma rays can travel thousands of feet in air and can easily pass through the human body.Gamma rays are emitted by unstable nuclei in their transition from a high energy state to a lower state known as gamma decay. In most practical laboratory sources, the excited nuclear states are created in the decay of a parent radionuclide, therefore a gamma decay typically accompanies other forms of decay, such as alpha or beta decay.Radiation and also gamma rays are all around us. In, around, and above the world we live in. It is a part of our natural world that has been here since the birth of our planet. Natural sources of gamma rays on Earth are inter alia gamma rays from naturally occurring radionuclides, particularly potassium-40.  Potassium-40 is a radioactive isotope of potassium which has a very long half-life of 1.251×10⁹ years (comparable to the age of Earth). This isotope can be found in soil, water also in meat and bananas. This is not the only example of natural source of gamma rays.

See also: Discovery of Gamma Rays

Characteristics of Gamma Rays / Radiation

Key features of gamma rays are summarized in following few points:

• Gamma rays are high-energy photons (about 10 000 times as much energy as the visible photons), the same photons as the photons forming the visible range of the electromagnetic spectrum – light.
• Photons (gamma rays and X-rays) can ionize atoms directly (despite they are electrically neutral) through the Photoelectric effect and the Compton effect, but secondary (indirect) ionization is much more significant.
• Gamma rays ionize matter primarily via indirect ionization.
• Although a large number of possible interactions are known, there are three key interaction mechanisms  with matter.
  • Photoelectric effect
  • Compton scattering
  • Pair production
• Gamma rays travel at the speed of light and they can travel thousands of meters in air before spending their energy.
• Since the gamma radiation is very penetrating matter, it must be shielded by very dense materials, such as lead or uranium.
• The distinction between X-rays and gamma rays is not so simple and has changed in recent decades.  According to the currently valid definition, X-rays are emitted by electrons outside the nucleus, while gamma rays are emitted by the nucleus.
• Gamma rays frequently accompany the emission of alpha and beta radiation.

Image: The relative importance of various processes of gamma radiation interactions with matter.

 

Photoelectric Effect

• The photoelectric effect dominates at low-energies of gamma rays.
• The photoelectric effect leads to the emission of photoelectrons from matter when light (photons) shines upon them.
• The maximum energy an electron can receive in any one interaction is hν.
• Electrons are only emitted by the photoelectric effect if photon reaches or exceeds a threshold energy.
• A free electron (e.g. from atomic cloud) cannot absorb entire energy of the incident photon. This is a result of the need to conserve both momentum and energy.
• The cross-section for the emission of n=1 (K-shell) photoelectrons is higher than that of n=2 (L-shell) photoelectrons. This is a result of the need to conserve momentum and energy.

See also: Albert Einstein and the Photoelectric Effect

Definition of Photoelectric effect

In the photoelectric effect, a photon undergoes an interaction with an electron which is bound in an atom. In this interaction the incident photon completely disappears and an energetic photoelectron is ejected by the atom from one of its bound shells. The kinetic energy of the ejected photoelectron (E_e) is equal to the incident photon energy (hν) minus the binding energy of the photoelectron in its original shell (E_b).

E_e=hν-E_b

Therefore photoelectrons are only emitted by the photoelectric effect if photon reaches or exceeds a threshold energy – the binding energy of the electron – the work function of the material. For gamma rays with energies of more than hundreds keV, the photoelectron carries off the majority of the incident photon energy – hν.

Following a photoelectric interaction, an ionized absorber atom is created with a vacancy in one of its bound shells. This vacancy is will be quickly filled by an electron from a shell with a lower binding energy (other shells) or through capture of a free electron from the material. The rearrangement of electrons from other shells creates another vacancy, which, in turn, is filled by an electron from an even lower binding energy shell. Therefore a cascade of more characteristic X-rays can be also generated. The probability of characteristic x-ray emission decreases as the atomic number of the absorber decreases. Sometimes , the emission of an Auger electron occurs.

 

Cross-Sections of Photoelectric Effect

At small values of gamma ray energy the photoelectric effect dominates. The mechanism is also enhaced for materials of high atomic number Z. It is not simple to derive analytic expression for the probability of photoelectric absorption of gamma ray per atom over all ranges of gamma ray energies. The probability of photoelectric absorption per unit mass is approximately proportional to:

τ_{(photoelectric)} = constant x Z^N/E^3.5

where Z is the atomic number, the exponent n varies between 4 and 5. E is the energy of the incident photon. The proportionality to higher powers of the atomic number Z is the main reason for using of high Z materials, such as lead or depleted uranium in gamma ray shields.

Although the probability of the photoelectric absorption of gamma photon decreases, in general, with increasing photon energy, there are sharp discontinuities in the cross-section curve. These are called “absoption edges” and they correspond to the binding energies of electrons from atom’s bound shells. For photons with the energy just above the edge, the photon energy is just sufficient to undergo the photoelectric interaction with electron from  bound shell, let say K-shell. The probability of such interaction is just above this edge much greater than that of photons of energy slightly below this edge. For gamma photons below this edge the interaction with electron from K-shell in energetically impossible and therefore the probability drops abruptly. These edges occur also at binding energies of electrons from other shells (L, M, N …..).

Compton Scattering

Key characteristics of Compton Scattering

• Compton scattering dominates at intermediate energies.
• It is the scattering of photons by atomic electrons  
• Photons undergo a wavelength shift called the Compton shift.
• The energy transferred to the recoil electron can vary from zero to a large fraction of the incident gamma ray energy

Definition of Compton Scattering

Compton scattering is the inelastic or nonclassical scattering of a photon (which may be an X-ray or gamma ray photon) by a charged particle, usually an electron. In Compton scattering, the incident gamma ray photon is deflected through an angle Θ with respect to its original direction. This deflection results in a decrease in energy (decrease in photon’s frequency) of the photon and is called the Compton effect. The photon transfers a portion of its energy to the recoil electron. The energy transferred to the recoil electron can vary from zero to a large fraction of the incident gamma ray energy, because all angles of scattering are possible. The Compton scattering was observed by A. H.Compton in 1923 at Washington University in St. Louis. Compton earned the Nobel Prize in Physics in 1927 for this new understanding about the particle-nature of photons.

Compton Scattering Formula

The Compton formula was published in 1923 in the Physical Review. Compton explained that the X-ray shift is caused by particle-like momentum of photons. Compton scattering formula is the mathematical relationship between the shift in wavelength and the scattering angle of the X-rays. In the case of Compton scattering the photon of frequency f collides with an electron at rest. Upon collision, the photon bounces off electron, giving up some of its initial energy (given by Planck’s formula E=hf), While the electron gains momentum (mass x velocity), the photon cannot lower its velocity. As a result of momentum conservetion law, the photon must lower its momentum given by:

So the decrease in photon’s momentum must be translated into decrease in frequency (increase in wavelength Δλ = λ’ – λ). The shift of the wavelength increased with scattering angle according to the Compton formula:

where

λ is the initial wavelength of photon

λ’ is the wavelength after scattering,

h is the Planck constant = 6.626 x 10^-34 J.s

m_e is the electron rest mass (0.511 MeV)

c is the speed of light

Θ is the scattering angle.

The minimum change in wavelength (λ′ − λ) for the photon occurs when Θ = 0° (cos(Θ)=1) and is at least zero. The maximum change in wavelength (λ′ − λ) for the photon occurs when Θ = 180° (cos(Θ)=-1). In this case the photon transfers to the electron as much momentum as possible.The maximum change in wavelength can be derived from Compton formula:

The quantity h/m_ec is known as the Compton wavelength of the electron and is equal to 2.43×10⁻¹² m.

Compton Scattering – Cross-Sections

The probability of Compton scattering per one interaction with an atom increases linearly with atomic number Z, because it depends on the number of electrons, which are available for scattering in the target atom. The angular distribution of photons scattered from a single free electron is described by the Klein-Nishina formula:

where ε = E₀/m_ec² and r₀ is the “classical radius of the electron” equal to about 2.8 x 10^-13 cm. The formula gives the probability of scattering a photon into the solid angle element dΩ = 2π sin Θ dΘ when the incident energy is E₀.

 

Compton Edge

In spectrophotometry, the Compton edge is a feature of the spectrograph that results from the Compton scattering in the scintillator or detector. This feature is due to photons that undergo Compton scattering with a scattering angle of 180° and then escape the detector. When a gamma ray scatters off the detector and escapes, only a fraction of its initial energy can be deposited in the sensitive layer of the detector. It depends on the scattering angle of the photon, how much energy will be deposited in the detector. This leads to a spectrum of energies. The Compton edge energy corresponds to full backscattered photon.

Inverse Compton Scattering

Inverse Compton scattering is the scattering of low energy photons to high energies by relativistic electrons. Relativistic electrons can boost energy of low energy photons by a potentially enormous amount (even gamma rays can be produced). This phenomenon is very important in astrophysics.

 

Alpha particles

Interaction of Alpha Particles with Matter

Since the electromagnetic interaction extends over some distance, it is not necessary for an alpha particles to make a direct collision with an atom. They can transfer energy simply by passing close by. Alpha particles interact with matter primarily through coulomb forces between their positive charge and the negative charge of the electrons from atomic orbitals. In general, the alpha particles (like other charged particles) transfer energy mostly by:

• Excitation. The charged particle can transfer energy to the atom, raising electrons to a higher energy levels.
• Ionization. Ionization can occur, when the charged particle have enough energy to remove an electron. This results in a creation of ion pairs in surrounding matter.

Creation of pairs requires energy, which is lost from the kinetic energy of the alpha particle causing it to decelerate. The positive ions and free electrons created by the passage of the alpha particle will then reunite, releasing energy in the form of heat (e.g. vibrational energy or rotational energy of atoms). There are considerable differences in the ways of energy loss and scattering between the passage of light charged particles such as positrons and electrons and heavy charged particles such as fission fragments, alpha particles, muons. Most of these differences are based on the different dynamics of the collision process. In general, when a heavy particle collides with a much lighter particle (electrons in the atomic orbitals), the laws of energy and momentum conservation predict that only a small fraction of the massive particle’s energy can be transferred to the less massive particle. The actual amount of transferred energy depends on how closely the charged particles passes through the atom and it depends also on restrictions from quantisation of energy levels.

See also: Interaction of Heavy Charged Particles with Matter

Stopping Power – Bethe Formula

A convenient variable that describes the ionization properties of surrounding medium is the stopping power. The linear stopping power of material is defined as the ratio of the differential energy loss for the particle within the material to the corresponding differential path length:

,where T is the kinetic energy of the charged particle, n_ion is the number of electron-ion pairs formed per unit path length, and I denotes the average energy needed to ionize an atom in the medium. For charged particles, S increases as the particle velocity decreases. The classical expression that describes the specific energy loss is known as the Bethe  formula. The non-relativistic formula was found by Hans Bethe in 1930. The relativistic version (see below) was found also by  Hans Bethe in 1932.

In this expression, m is the rest mass of the electron, β equals to v/c, what expresses the particle’s velocity relative to the speed of light, γ is the Lorentz factor of the particle, Q equals to its charge, Z is the atomic number of the medium and n is the atoms density in the volume. For nonrelativistic particles (heavy charged particles are mostly nonrelativistic), dT/dx is dependent on 1/v². This is can be explained by the greater time the charged particle spends in the negative field of the electron, when the velocity is low.

The stopping power of most materials is very high for heavy charged particles and these particles have very short ranges. For example, the range of a 5 MeV alpha particle is approximately only 0,002 cm in aluminium alloy. Most alpha particles can be stopped by an ordinary sheet of paper or living tissue. Therefore the shielding of alpha particles does not pose a difficult problem, but on the other hand alpha radioactive nuclides can lead to serious health hazards when they are ingested or inhaled (internal contamination).

Bragg Curve

The Bragg curve is typical for alpha particles and for other heavy charged particles and describes energy loss of ionizing radiation during travel through matter. For this curve is typical the Bragg peak, which is the result of 1/v² dependency of the stopping power. This peak occurs because the cross section of interaction increases immediately before the particle come to rest. For most of the track, the charge remains unchanged and the specific energy loss increases according to the 1/v². Near the end of the track, the charge can be reduced through electron pickup and the curve can fall off.

The Bragg curve also differs somewhat due to the effect of straggling. For a given material the range will be the nearly the same for all particles of the same kind with the same initial energy. Because the details of the microscopic interactions undergone by any specific particle vary randomly, a small variation in the range can be observed. This variation is called straggling and it is caused by the statistical nature of the energy loss process which consists of a large number of individual collisions.

This phenomenon, which is described by the Bragg curve, is exploited in particle therapy of cancer, because this allows to concentrate the stopping energy on the tumor while minimizing the effect on the surrounding healthy tissue.

See also:

Neutron

See also:

Fundamental Particles

See also:

Beta Particle

What is Neutron

A neutron is one of the subatomic particles that make up matter. In the universe, neutrons are abundant, making up more than half of all visible matter. It has no electric charge and a rest mass equal to 1.67493 × 10−27 kg—marginally greater than that of the proton but nearly 1839 times greater than that of the electron. The neutron has a mean square radius of about 0.8×10−15 m, or 0.8 fm, and it is a spin-½ fermion.

The neutrons exist in the nuclei of typical atoms, along with their positively charged counterparts, the protons. Neutrons and protons, commonly called nucleons, are bound together in the atomic nucleus, where they account for 99.9 percent of the atom’s mass. Research in high-energy particle physics in the 20th century revealed that neither the neutron nor the proton is not the smallest building block of matter. Protons and neutrons have also their structure. Inside the protons and neutrons, we find true elementary particles called quarks. Within the nucleus, protons and neutrons are bound together through the strong force, a fundamental interaction that governs the behaviour of the quarks that make up the individual protons and neutrons.

A nuclear stability is determined by the competition between two fundamental interactions. Protons and neutrons are attracted each other via strong force. On the other hand protons repel each other via the electric force due to their positive charge. Therefore neutrons within the nucleus act somewhat like nuclear glue, neutrons attract each other and protons , which helps offset the electrical repulsion between protons. There are only certain combinations of neutrons and protons, which forms stable nuclei. For example, the most common nuclide of the common chemical element lead (Pb) has 82 protons and 126 neutrons.

Because of the strength of the nuclear force at short distances, the nuclear binding energy (the energy required to disassemble a nucleus of an atom into its component parts) of nucleons is more than seven orders of magnitude larger than the electromagnetic energy binding electrons in atoms. Nuclear reactions (such as nuclear fission or nuclear fusion) therefore have an energy density that is more than 10 000 000x that of chemical reactions.
Knowledge of the behaviour and properties of neutrons is essential to the production of nuclear power. Shortly after the neutron was discovered in 1932, it was quickly realized that neutrons might act to form a nuclear chain reaction. When nuclear fission was discovered in 1938, it became clear that, if a fission reaction produced free neutrons, each of these neutrons might cause further fission reaction in a cascade known as a chain reaction. Knowledge of cross-sections (the key parameter representing probability of interaction between a neutron and a nucleus) became crutial for design of reactor cores and the first nuclear weapon (Trinity, 1945).

Structure of the Neutron

Neutrons and protons are classified as hadrons, subatomic particles that are subject to the strong force and as baryons since they are composed of three quarks. The neutron is a composite particle made of two down quarks with charge −⅓  e and one up quark with charge +⅔ e. Since the neutron has no net electric charge, it is not affected by eletric forces, but the neutron does have a slight distribution of electric charge within it. This results in non-zero magnetic moment (dipole moment) of the neutron. Therefore the neutron interacts also via electromagnetic interaction, but much weaker than the proton.

The mass of the neutron is 939.565 MeV/c², whereas the mass of the three quarks is only about 12 MeV/c² (only about 1% of the mass-energy of the neutron). Like the proton, most of mass (energy) of the neutron is in the form of the strong nuclear force energy (gluons). The quarks of the neutron are held together by gluons, the exchange particles for the strong nuclear force. Gluons carry the color charge of the strong nuclear force.

See also: Structure of the Neutron

Properties of the Neutron

Key properties of neutrons are summarized below:

• Mean square radius of a neutron is ~ 0.8 x 10^-15m (0.8 fermi)
• The mass of the neutron is 939.565 MeV/c²
• Neutrons are ½ spin particles – fermionic statistics
• Neutrons are neutral particles – no net electric charge.
• Neutrons have non-zero magnetic moment.
• Free neutrons (outside a nucleus) are unstable and decay via beta decay. The decay of the neutron involves the weak interaction and is associated with a quark transformation (a down quark is converted to an up quark).
• Mean lifetime of a free neutron is 882 seconds (i.e. half-life is 611 seconds ).
• A natural neutron background of free neutrons exists everywhere on Earth and it is caused by muons produced in the atmosphere, where high energy cosmic rays collide with particles of Earth’s atmosphere.
• Neutrons cannot directly cause ionization. Neutrons ionize matter only indirectly.
• Neutrons can travel hundreds of feet in air without any interaction. Neutron radiation is highly penetrating.
• Neutrons trigger the nuclear fission.
• The fission process produces free neutrons (2 or 3).
• Thermal or cold neutrons have the wavelengths similar to atomic spacings. They can be used in neutron diffraction experiments to determine the atomic and/or magnetic structure of a material.

See also: Properties of the Neutron

 

Detection of Neutrons

Since the neutrons are electrically neutral particles, they are mainly subject to strong nuclear forces but not to electric forces. Therefore neutrons are not directly ionizing and they have usually to be converted into charged particles before they can be detected. Generally every type of neutron detector must be equipped with converter (to convert neutron radiation to common detectable radiation) and one of the conventional radiation detectors (scintillation detector, gaseous detector, semiconductor detector, etc.).

Neutron converters

Two basic types of neutron interactions with matter are for this purpose available:

• Elastic scattering. The free neutron can be scattered by a nucleus, transferring some of its kinetic energy to the nucleus. If the neutron has enough energy to scatter off nuclei the recoiling nucleus ionizes the material surrounding the converter. In fact, only hydrogen and helium nuclei are light enough for practical application. Charge produced in this way can be collected by the conventional detector to produce a detected signal. Neutrons can transfer more energy to light nuclei. This method is appropriate for detecting fast neutrons (fast neutrons do not have high cross-section for absorption) allowing detection of fast neutrons without a moderator.
• Neutron absorption. This is a common method allowing detection of neutrons of entire energy spectrum. This method is is based on variety of absorption reactions (radiative capture, nuclear fission, rearrangement reactions, etc.). The neutron is here absorbed by target material (converter) emitting secondary particles such as protons, alpha particles, beta particles, photons (gamma rays) or fission fragments. Some reactions are threshold reactions (requiring a minimum energy of neutrons), but most of reactions occurs at epithermal and thermal energies. That means the moderation of fast neutrons is required leading in poor energy information of the neutrons. Most common nuclei for the neutron converter material are:
  • ¹⁰B(n,α). Where the neutron capture cross-section for thermal neutrons is σ = 3820 barns and the natural boron has abundance of ¹⁰B 19,8%.
  • ³He(n,p). Where the neutron capture cross-section for thermal neutrons is σ = 5350 barns and the natural helium has abundance of ³He 0.014%.
  • ⁶Li(n,α). Where the neutron capture cross-section for thermal neutrons is σ = 925 barns and the natural lithium has abundance of ⁶Li 7,4%.
  • ¹¹³Cd(n,ɣ). Where the neutron capture cross-section for thermal neutrons is σ = 20820 barns and the natural cadmium has abundance of ¹¹³Cd 12,2%.
  • ²³⁵U(n,fission). Where the fission cross-section for thermal neutrons is σ = 585 barns and the natural uranium has abundance of ²³⁵U 0.711%. Uranium as a converter produces fission fragments which are heavy charged particles. This have significant advantage. The heavy charged particles (fission fragments) create a high output signal, because the fragments deposit a large amount of energy in a detector sensitive volume. This allows an easy discrimination of the background radiation (e.i. gamma radiation). This important feature can be used for example in a nuclear reactor power measurement, where the neutron field is accompanied  by a significant gamma background.

See also: Detection of Neutrons

Neutron Sources

A neutron source is any device that emits neutrons. Neutron sources have many applications, they can be used in research, engineering, medicine, petroleum exploration, biology, chemistry and nuclear power. A neutron source is characterized by a number of factors:

• Significance of the source
• Intensity. The rate of neutrons emitted by the source.
• Energy distribution of emitted neutrons.
• Angular distribution of emitted neutrons.
• Mode of emission. Continuous or pulsed operation.

Classification by significance of the source

• Large (Significant) neutron sources
  • Nuclear Reactors. There are nuclei that can undergo fission on their own spontaneously, but only certain nuclei, like uranium-235, uranium-233 and plutonium-239, can sustain a fission chain reaction. This is because these nuclei release neutrons when they break apart, and these neutrons can induce fission of other nuclei. Uranium-235 which exists as 0.7% of naturally occurring uranium undergoes nuclear fission with thermal neutrons with the production of, on average, 2.4 fast neutrons and the release of ~ 180 MeV of energy per fission. Free neutrons released by each fission play very important role as a trigger of the reaction, but they can be also used fo another purpose. For example: One neutron is required to trigger a further fission. Part of free neutrons (let say 0.5 neutrons/fission) is absorbed in other material, but an excess of neutrons (0.9 neutrons/fission) is able to leave the surface of the reactor core and can be used as a neutron source.

• • Fusion Systems. Nuclear fusion is a nuclear reaction in which two or more atomic nuclei (e.g. D+T) collide at a very high energy and fuse together. Thy byproduct of DT fusion is a free neutron (see picture), therefore also nuclear fusion reaction has the potential to produces large quantities of neutrons.
  • Spallation Sources. A spallation source is a high-flux neutron source in which protons that have been accelerated to high energies hit a heavy target material, causing the emission of neutrons. The reaction occurs above a certain energy threshold for the incident particle, which is typically 5 – 15 MeV.

• Medium neutron sources
  • Bremssstrahlung from Electron Accelerators / Photofission. Energetic electrons when slowed down rapidly in a heavy target emit intense gamma radiation during the deceleration process. This is known as Bremsstrahlung or braking radiation. The interaction of the gamma radiation with the target produces neutrons via the (γ,n) reaction, or the (γ,fission) reaction when a fissile target is used. e-→Pb → γ→ Pb →(γ,n) and (γ,fission). The Bremsstrahlung γ energy exceeds the binding energy of the “last” neutron in the target. A source strength of 10¹³ neutrons/second produced in short (i.e. < 5 μs) pulses can be readily realised.
  • Dense plasme focus. The dense plasma focus (DPF) is a device that is known as an efficient source of neutrons from fusion reactions. Mechanism of dense plasma focus (DPF) is based on nuclear fusion of short-lived plasma of deuterium and/or tritium. This device produces a short-lived plasma by electromagnetic compression and acceleration that is called a pinch. This plasma is during the pinch hot and dense enough to cause nuclear fusion and the emission of neutrons.
  • Light ion accelerators. Neutrons can be also produced by particle accelerators using targets of deuterium, tritium, lithium, beryllium, and other low-Z materials. In this case the target must be bombarded with accelerated hydrogen (H), deuterium (D), or tritium (T) nuclei.

• Small neutron sources
  • Neutron Generators. Neutrons are produced in the fusion of deuterium and tritium in the following exothermic reaction. ²D + ³T → ⁴He + n + 17.6 MeV.  The neutron is produced with a kinetic energy of 14.1 MeV. This can be achieved on a small scale in the laboratory with a modest 100 kV accelerator for deuterium atoms bombarding a tritium target. Continuous neutron sources of ~10¹¹ neutrons/second can be achieved relatively simply.
  • Radioisotope source – (α,n) reactions. In certain light isotopes the ‘last’ neutron in the nucleus is weakly bound and is released when the compound nucleus formed following α-particle bombardment decays. The bombardment of beryllium by α-particles leads to the production of neutrons by the following exothermic reaction: ⁴He + ⁹Be→¹²C + n + 5.7 MeV. This reaction yields a weak source of neutrons with an energy spectrum resembling that from a fission source and is used nowadays in portable neutron sources. Radium, plutonium or americium can be used as an α-emitter.
  • Radioisotope source – (γ,n) reactions. (γ,n) reactions can also be used for the same purpose. In this type of source, because of the greater range of the γ-ray, the two physical  components of the source can be separated making it possible to ‘switch off’ the reaction if so required by removing the radioactive source from the beryllium. (γ,n) sources produce a monoenergetic neutrons unlike (α,n) sources.  The (γ,n) source uses antimony-124 as the gamma emitter in the following endothermic reaction.

¹²⁴Sb→¹²⁴Te + β− + γ

γ + ⁹Be→⁸Be + n – 1.66 MeV

• • Radioisotope source – spontaneous fission. Certain isotopes undergo spontaneous fission with emission of neutrons. The most commonly used spontaneous fission source is the radioactive isotope californium-252. Cf-252 and all other spontaneous fission neutron sources are produced by irradiating uranium or another transuranic element in a nuclear reactor, where neutrons are absorbed in the starting material and its subsequent reaction products, transmuting the starting material into the SF isotope.

See also: Neutron Sources

See also: Source Neutrons

,where T is the kinetic energy of the charged particle, n_ion is the number of electron-ion pairs formed per unit path length, and I denotes the average energy needed to ionize an atom in the medium. For charged particles, S increases as the particle velocity decreases. The classical expression that describes the specific energy loss is known as the Bethe  formula. The non-relativistic formula was found by Hans Bethe in 1930. The relativistic version (see below) was found also by  Hans Bethe in 1932.

In this expression, m is the rest mass of the electron, β equals to v/c, what expresses the particle’s velocity relative to the speed of light, γ is the Lorentz factor of the particle, Q equals to its charge, Z is the atomic number of the medium and n is the atoms density in the volume. For nonrelativistic particles (heavy charged particles are mostly nonrelativistic), dT/dx is dependent on 1/v². This is can be explained by the greater time the charged particle spends in the negative field of the electron, when the velocity is low.

The stopping power of most materials is very high for heavy charged particles and these particles have very short ranges. For example, the range of a 5 MeV alpha particle is approximately only 0,002 cm in aluminium alloy. Most alpha particles can be stopped by an ordinary sheet of paper or living tissue. Therefore the shielding of alpha particles does not pose a difficult problem, but on the other hand alpha radioactive nuclides can lead to serious health hazards when they are ingested or inhaled (internal contamination).

Specifics of Fission Fragments

The fission fragments three two key features (somewhat different from alpha particles or protons), which influence their energy loss during its travel through matter.

• High initial energy. Results in a large effective charge.
• Large effective charge. The fission fragments start out with lack of many electrons, therefore their specific loss is greater than alpha’s specific loss, for example.
•  Immediate electron pickup. Results in changes of (-dE/dx) during the travel.

These features results  in the continuous decrease in the effective charge carried by the fission fragment as the fragment comes to rest and continuous decrease in -dE/dx. The resulting decrease in -dE/dx (from the electron pickup) is larger than the increase that accompanies a reduction in velocity. The range of typical fission fragment can be approximately half that of a 5 MeV alpha particle.

See also:

Interaction of Heavy Charged Particles with Matter

See also:

The Bragg curve is typical for heavy charged particles and describes energy loss of ionizing radiation during travel through matter. For this curve is typical the Bragg peak, which is the result of 1/v² dependency of the stopping power. This peak occurs because the cross section of interaction increases immediately before the particle come to rest. For most of the track, the charge remains unchanged and the specific energy loss increases according to the 1/v². Near the end of the track, the charge can be reduced through electron pickup and the curve can fall off.

The Bragg curve also differs somewhat due to the effect of straggling. For a given material the range will be the nearly the same for all particles of the same kind with the same initial energy. Because the details of the microscopic interactions undergone by any specific particle vary randomly, a small variation in the range can be observed. This variation is called straggling and it is caused by the statistical nature of the energy loss process which consists of a large number of individual collisions.

This phenomenon, which is described by the Bragg curve, is exploited in particle therapy of cancer, because this allows to concentrate the stopping energy on the tumor while minimizing the effect on the surrounding healthy tissue.

See also:

Stopping Power – Bethe Formula

See also:

Interaction of Heavy Charged Particles with Matter

See also:

Description Beta Particles

Beta particles are high-energy, high-speed electrons or positrons emitted by certain fission fragments or by certain primordial radioactive nuclei such as potassium-40. The beta particles are a form of ionizing radiation also known as beta rays. The production of beta particles is termed beta decay. There are two forms of beta decay, the electron decay (β− decay) and the positron decay (β+ decay). In a nuclear reactor occurs especially the β− decay, because the common feature of the fission products is an excess of neutrons (see Nuclear Stability). An unstable fission fragment with the excess of neutrons undergoes β− decay, where the neutron is converted into a proton, an electron, and an electron antineutrino.

Spectrum of beta particles

In the process of beta decay, either an electron or a positron is emitted. This emission is accompanied by the emission of antineutrino (β- decay) or neutrino (β+ decay), which shares energy and momentum of the decay. The beta emission has a characteristic spectrum. This characteristic spectrum is caused by the fact that either a neutrino or an antineutrino is emitted with emission of beta particle. The shape of this energy curve depends on what fraction of the reaction energy (Q value-the amount of energy released by the reaction) is carried by the massive particle. Beta particles can therefore be emitted with any kinetic energy ranging from 0 to Q. By 1934, Enrico Fermi had developed a Fermi theory of beta decay, which predicted the shape of this energy curve.

Nature of Interaction of Beta Radiation with Matter

Summary of types of interactions:

• Inelastic collisions with atomic electrons (Excitation and Ionization)
• Elastic scattering off nuclei
• Bremsstrahlung.
• Cherenkov radiation.
• Annihilation (only positrons)

Nature of an interaction of a beta radiation with matter is different from the alpha radiation, despite the fact that beta particles are also charged particles. In comparison with alpha particles, beta particles have much lower mass and they reach mostly relativistic energies. Their mass is equal to the mass of the orbital electrons with which they are interacting and unlike the alpha particle a much larger fraction of its kinetic energy can be lost in a single interaction. Since the beta particles mostly reach relativistic energies, the nonrelativistic Bethe formula cannot be used. For high energy electrons an similar expression has also been derived by Bethe to describe the specific energy loss due to excitation and ionization (the “collisional losses”).

Moreover, beta particles can interact via electron-nuclear interaction (elastic scattering off nuclei), which can significantly change the direction of beta particle. Therefore their path is not so straightforward. The beta particles follow a very zig-zag path through absorbing material, this resulting path of particle is longer than the linear penetration (range) into the material.

Beta particles also differ from other heavy charged particles in the fraction of energy lost by radiative process known as the bremsstrahlung. From classical theory, when a charged particle is accelerated or decelerated, it must radiate energy and the deceleration radiation is known as the bremsstrahlung (“braking radiation”).

There is another mechanism by which beta particles loss energy via production of electromagnetic radiation. When the beta particle moves faster than the speed of light (phase velocity) in the material it generates a shock wave of electromagnetic radiation known as the Cherenkov radiation.

Positrons interact similarly with matter when they are energetic. But when the positron comes to rest, it interacts with a negatively charged electron, resulting in the annihilation of the electron-positron pair.

Bremsstrahlung

The bremsstrahlung  is electromagnetic radiation produced by the acceleration or deceleration of a charged particle when deflected by magnetic fields (an electron by magnetic field of particle accelerator) or another charged particle (an electron by an atomic nucleus). The name bremsstrahlung comes from the German. The literal translation is ‘braking radiation’. From classical theory, when a charged particle is accelerated or decelerated, it must radiate energy.

The bremsstrahlung is one of possible interactions of light charged particles with matter (especially with high atomic numbers).

The two commonest occurrences of bremsstrahlung are by:

• Deceleration of charged particle. When charged particles enter a material they are decelerated by the electric field of the atomic nuclei and atomic electrons.
• Acceleration of charged particle. When ultra-relativistic charged particles move through magnetic fields they are forced to move along a curved path. Since their direction of motion is continually changing, they are also accelerating and so emit bremsstrahlung, in this case it is referred to as synchrotron radiation.

Since the bremsstrahlung is much stronger for lighter particles, this effect is much more important for beta particles than for protons, alpha particles, and heavy charged nuclei (fission fragments). This effect can be neglected at particle energies below about 1 MeV, because the energy loss due to bremsstrahlung is very small. Radiation loss starts to become important only at particle energies well above the minimum ionization energy. At relativistic energies the ratio of loss rate by bremsstrahlung to loss rate by ionization is approximately proportional to the product of the particle’s kinetic energy and the atomic number of the absorber.

The cross section of bremsstrahlung depends on mostly these terms:

So the ratio of stopping powers of bremsstrahlung and ionization losses is:

,where E is the particle’s (electron’s) kinetic energy, Z is the mean atomic number of the material and E’ is a proportionality constant; E’ ≈ 800 MeV. The kinetic energy at which energy loss by bremsstrahlung is equal to the energy loss by ionization and excitation (collisional losses) is called the critical energy. Another paremeter is the radiation length, defined as the distance over which the incident electron’s energy is reduced by a factor 1/e (0.37) due to radiation losses alone. Following table give some typical values:

Cherenkov Radiation

The cherenkov radiation is electromagnetic radiation emitted when a charged particle (such as an electron) moves through a dielectric medium faster than the phase velocity of light in that medium. It is similar to the bow wave produced by a boat travelling faster than the speed of water waves. Cherenkov radiation occurs only if the particle’s speed is higher than the phase velocity of light in the material. Even at high energies the energy lost by Cherenkov radiation is much less than that by the other mechanisms (collisions, bremsstrahlung). It is named after Soviet physicist Pavel Alekseyevich Cherenkov, who shared the Nobel Prize in physics in 1958 with Ilya Frank and Igor Tamm for the discovery of Cherenkov radiation, made in 1934.

Cherenkov radiation can be used to detect high-energy charged particles (especially beta particles). In nuclear reactors or in a spent nuclear fuel pool, beta particles (high-energy electrons) are released as the fission fragments decay. The glow is visible also after the chain reaction stops (in the reactor). The cherenkov radiation can characterize the remaining radioactivity of spent nuclear fuel, therefore it can be used for measuring of fuel burnup.

Positron Interactions

The coulomb forces that constitute the major mechanism of energy loss for electrons are present for either positive or negative charge on the particle and constitute the major mechanism of energy loss also for positrons. Whatever the interaction involves a repulsive or attractive force between the incident particle and orbital electron (or atomic nucleus), the impulse and energy transfer for particles of equal mass are about the same. Therefore positrons interact similarly with matter when they are energetic. The track of positrons in material is similar to the track of electrons. Even their specific energy loss and range are about the same for equal initial energies.

At the end of their path, positrons differ significantly from electrons. When a positron (antimatter particle) comes to rest, it interacts with an electron (matter particle), resulting in the annihilation of the both particles and the complete conversion of their rest mass to pure energy (according to the E=mc² formula) in the form of two oppositely directed 0.511 MeV gamma rays (photons).

Positron Annihilation

Electron–positron annihilation occurs when a negatively charged electron and a positively charged positron collide.When a low-energy electron annihilates a low-energy positron (antiparticle of electron), they can only produce two or more photons (gamma rays). The production of only one photon is forbidden because of conservation of linear momentum and total energy. The production of another particle is also forbidden because of both particles (electron-positron) together do not carry enough mass-energy to produce heavier particles. When an electron and a positron collide, they annihilate resulting in the complete conversion of their rest mass to pure energy (according to the E=mc² formula) in the form of two oppositely directed 0.511 MeV gamma rays (photons).

e⁻ + e⁺ → γ + γ (2x 0.511 MeV)

This process must satisfy a number of conservation laws, including:

• Conservation of electric charge. The net charge before and after is zero.
• Conservation of linear momentum and total energy. T
• Conservation of angular momentum.

See also:

Interaction of Heavy Charged Particles with Matter

See also:

Interaction of Radiation with Matter

See also:

Interaction of Gamma Radiation with Matter

Description Beta Particles

Beta particles are high-energy, high-speed electrons or positrons emitted by certain fission fragments or by certain primordial radioactive nuclei such as potassium-40. The beta particles are a form of ionizing radiation also known as beta rays. The production of beta particles is termed beta decay. There are two forms of beta decay, the electron decay (β− decay) and the positron decay (β+ decay). In a nuclear reactor occurs especially the β− decay, because the common feature of the fission products is an excess of neutrons (see Nuclear Stability). An unstable fission fragment with the excess of neutrons undergoes β− decay, where the neutron is converted into a proton, an electron, and an electron antineutrino.

Shielding of Beta Particles – Electrons

Beta radiation ionizes matter weaker than alpha radiation. On the other hand the ranges of beta particles are longer and depends strongly on initial kinetic energy of particle. Some have enough energy to be of concern regarding external exposure. A 1 MeV beta particle can travel approximately 3.5 meters in air. Such beta particles can penetrate into the body and deposit dose to internal structures near the surface. Therefore greater shielding than in case of alpha radiation is required.

Materials with low atomic number Z are appropriate as beta particle shields. With high Z materials the bremsstrahlung (secondary radiation – X-rays) is associated. This radiation is created during slowing down of beta particles while they travel in a very dense medium. Heavy clothing, thick cardboard or thin aluminium plate will provide protection from beta radiation and prevents of production of the bremsstrahlung.

See also calculator: Beta activity to dose rate 

Shielding of Beta Particles – Positrons

The coulomb forces that constitute the major mechanism of energy loss for electrons are present for either positive or negative charge on the particle and constitute the major mechanism of energy loss also for positrons. Whatever the interaction involves a repulsive or attractive force between the incident particle and orbital electron (or atomic nucleus), the impulse and energy transfer for particles of equal mass are about the same. Therefore positrons interact similarly with matter when they are energetic. The track of positrons in material is similar to the track of electrons. Even their specific energy loss and range are about the same for equal initial energies.

At the end of their path, positrons differ significantly from electrons. When a positron (antimatter particle) comes to rest, it interacts with an electron (matter particle), resulting in the annihilation of the both particles and the complete conversion of their rest mass to pure energy (according to the E=mc² formula) in the form of two oppositely directed 0.511 MeV gamma rays (photons).

Therefore any positron shield have to include also a gamma ray shield. In order to minimize the bremsstrahlung a multi-layered radiation shield is appropriate. Material for the first layer must fulfill the requirements for negative beta radiation shielding. First layer of such shield may be for example a thin aluminium plate (to shield positrons), while the second layer of such shield may be a dense material such as lead or depleted uranium.

See also:

Alpha Particle

See also:

Fundamental Particles

See also: