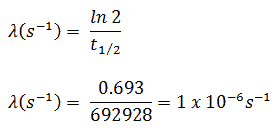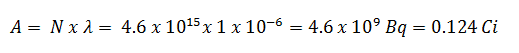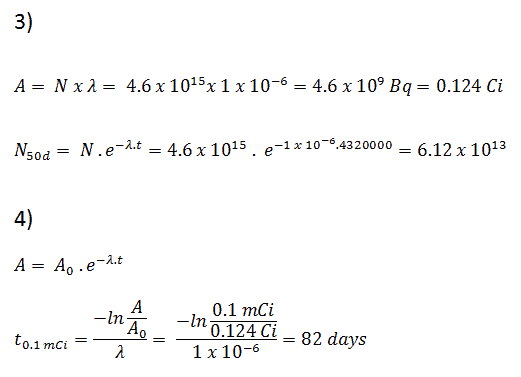 La ley de desintegración radiactiva es una ley universal que describe el comportamiento estadístico de una gran cantidad de nucleidos.
La ley de desintegración radiactiva es una ley universal que describe el comportamiento estadístico de una gran cantidad de nucleidos.
Como se escribió, la desintegración radiactiva es un proceso aleatorio a nivel de átomos individuales, ya que, según la teoría cuántica, es imposible predecir cuándo se desintegrará un átomo en particular. En otras palabras, el núcleo de un radionúclido no tiene «memoria». Un núcleo no «envejece» con el paso del tiempo. Por lo tanto, la probabilidad de que se rompa no aumenta con el tiempo, sino que se mantiene constante sin importar cuánto tiempo haya existido el núcleo. Durante su desintegración impredecible, este núcleo inestable se descompone espontáneamente y al azar para formar un núcleo diferente (o un estado de energía diferente: desintegración gamma), emitiendo radiación en forma de particiones atómicas o rayos de alta energía.
Los cálculos de la desintegración de los núcleos radiactivos son relativamente sencillos, debido al hecho de que solo hay una ley fundamental que rige todo el proceso de desintegración.
La ley de desintegración radiactiva establece que la probabilidad por unidad de tiempo de que un núcleo decaiga es una constante, independiente del tiempo. Esta constante se llama la constante de desintegración y se denota por λ, «lambda». Esta probabilidad constante puede variar mucho entre los diferentes tipos de núcleos, lo que lleva a las diferentes tasas de desintegración observadas. La desintegración radiactiva de cierto número de átomos (masa) es exponencial en el tiempo.
Ley de desintegración radiactiva: N = Ne -λt
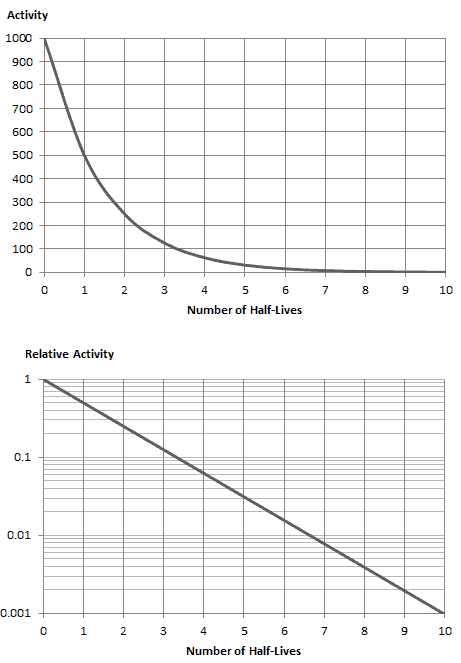
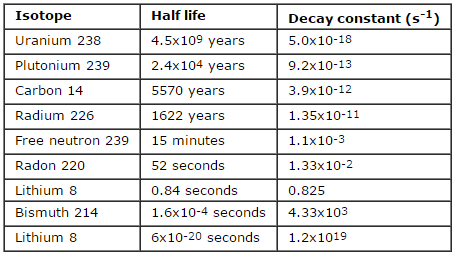
La tasa de desintegración nuclear también se mide en términos de vidas medias . La vida media es la cantidad de tiempo que le toma a un isótopo dado perder la mitad de su radioactividad. Si un radioisótopo tiene una vida media de 14 días, la mitad de sus átomos se habrán descompuesto en 14 días. En 14 días más, la mitad de la mitad restante se descompondrá, y así sucesivamente. Las vidas medias varían desde millonésimas de segundo para productos de fisión altamente radiactivos hasta miles de millones de años para materiales de larga duración (como el uranio natural). Darse cuenta delas vidas medias cortas van con grandes constantes de descomposición. El material radiactivo con una vida media corta es mucho más radiactivo (en el momento de la producción) pero obviamente perderá su radiactividad rápidamente. No importa qué tan larga o corta sea la vida media, después de que hayan pasado siete vidas medias, queda menos del 1 por ciento de la actividad inicial.
La ley de desintegración radiactiva se puede derivar también para cálculos de actividad o cálculos de masa de material radiactivo:
(Número de núcleos) N = Ne -λt (Actividad) A = Ae -λt (Masa) m = me -λt
, donde N (número de partículas) es el número total de partículas en la muestra, A (actividad total) es el número de desintegraciones por unidad de tiempo de una muestra radiactiva, m es la masa del material radiactivo restante.
Actividad – Actividad específica
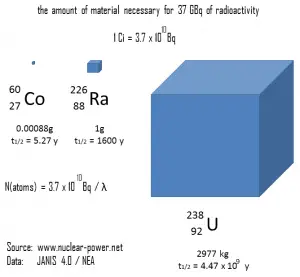 Una medida de radiactividad (actividad) se basa en el conteo de desintegraciones por segundo . La unidad de actividad del SI es el becquerel (Bq), igual a un segundo recíproco. La actividad depende solo del número de desintegraciones por segundo, no del tipo de desintegración, la energía de los productos de desintegración o los efectos biológicos de la radiación. Se puede utilizar para caracterizar la tasa de emisión de radiación ionizante. Actividad específicaes la actividad por cantidad de un radionúclido, por lo tanto, la actividad específica se define como la actividad por cantidad de átomos de un radionúclido particular. Por lo general, se administra en unidades de Bq / g, pero otra unidad de actividad de uso común es el curie (Ci) que permite la definición de actividad específica en Ci / g.
Una medida de radiactividad (actividad) se basa en el conteo de desintegraciones por segundo . La unidad de actividad del SI es el becquerel (Bq), igual a un segundo recíproco. La actividad depende solo del número de desintegraciones por segundo, no del tipo de desintegración, la energía de los productos de desintegración o los efectos biológicos de la radiación. Se puede utilizar para caracterizar la tasa de emisión de radiación ionizante. Actividad específicaes la actividad por cantidad de un radionúclido, por lo tanto, la actividad específica se define como la actividad por cantidad de átomos de un radionúclido particular. Por lo general, se administra en unidades de Bq / g, pero otra unidad de actividad de uso común es el curie (Ci) que permite la definición de actividad específica en Ci / g.
Las unidades de actividad (el curie y el becquerel) también se pueden usar para caracterizar una cantidad total de liberaciones controladas o accidentales de átomos radiactivos .
Unidades de actividad
- Bequerel . El becquerel es una unidad SI de radioactividad definida en 1974. Se nombra en honor a Henri Becquerel, un físico francés que descubrió la radioactividad en 1896. Un becquerel (1Bq) es igual a 1 desintegración por segundo .
- Curie . El curie es una unidad de radioactividad no SIdefinida en 1910. Originalmente se definió como equivalente al número de desintegraciones quesufrirá un gramo de radio-226 en un segundo . Actualmente, un curie se define como 1Ci = 3.7 x 10 10 desintegraciones por segundo .
- Rutherford . Rutherford (símbolo Rd ) también es una unidad no SI definida como la actividad de una cantidad de material radiactivo en el que se desintegra un millón de núcleos por segundo .
Decadencia constante y vida media
En los cálculos de radioactividad, se debe conocer uno de los dos parámetros ( constante de desintegración o vida media ), que caracterizan la tasa de desintegración. Existe una relación entre la vida media (t 1/2 ) y la constante de desintegración λ. La relación puede derivarse de la ley de descomposición estableciendo N = ½ N o . Esto da:
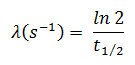 donde ln 2 (el logaritmo natural de 2) es igual a 0.693. Si se da la constante de desintegración (λ), es fácil calcular la vida media, y viceversa.
donde ln 2 (el logaritmo natural de 2) es igual a 0.693. Si se da la constante de desintegración (λ), es fácil calcular la vida media, y viceversa.
Ecuaciones de Bateman
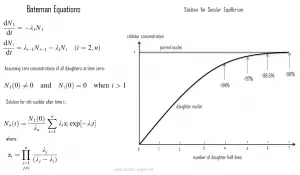 En física, las ecuaciones de Bateman son un conjunto de ecuaciones diferenciales de primer orden, que describen la evolución en el tiempo de las concentraciones de nucleidos en cadena de desintegración lineal o en serie. El modelo fue formulado por Ernest Rutherford en 1905 y la solución analítica para el caso de desintegración radiactiva en una cadena lineal fue provista por Harry Bateman en 1910. Este modelo también puede usarse en códigos de agotamiento nuclear para resolver problemas de desintegración y transmutación nuclear.
En física, las ecuaciones de Bateman son un conjunto de ecuaciones diferenciales de primer orden, que describen la evolución en el tiempo de las concentraciones de nucleidos en cadena de desintegración lineal o en serie. El modelo fue formulado por Ernest Rutherford en 1905 y la solución analítica para el caso de desintegración radiactiva en una cadena lineal fue provista por Harry Bateman en 1910. Este modelo también puede usarse en códigos de agotamiento nuclear para resolver problemas de desintegración y transmutación nuclear.
Por ejemplo, ORIGEN es un sistema de código de computadora para calcular la acumulación, descomposición y procesamiento de materiales radiactivos. ORIGEN utiliza un método exponencial matricial para resolver un gran sistema de ecuaciones diferenciales ordinarias acopladas, lineales y de primer orden (similar a las ecuaciones de Bateman ) con coeficientes constantes.
Las ecuaciones de Bateman para el caso de desintegración radiactiva de la serie n – nucleidos en cadena lineal que describe las concentraciones de nucleidos son las siguientes que se muestran en la figura.
Ejemplo: Ley de descomposición radiactiva
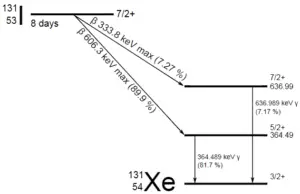 Una muestra de material contiene 1 microgramo de yodo-131. Tenga en cuenta que el yodo-131 desempeña un papel importante como isótopo radiactivo presente en los productos de fisión nuclear , y es un importante contribuyente a los riesgos para la salud cuando se libera a la atmósfera durante un accidente. El yodo 131 tiene una vida media de 8.02 días.
Una muestra de material contiene 1 microgramo de yodo-131. Tenga en cuenta que el yodo-131 desempeña un papel importante como isótopo radiactivo presente en los productos de fisión nuclear , y es un importante contribuyente a los riesgos para la salud cuando se libera a la atmósfera durante un accidente. El yodo 131 tiene una vida media de 8.02 días.
Calcular:
- El número de átomos de yodo-131 inicialmente presentes.
- La actividad del yodo-131 en curies.
- El número de átomos de yodo-131 que permanecerán en 50 días.
- El tiempo que le llevará a la actividad alcanzar 0.1 mCi.
Solución:
- El número de átomos de yodo-131 se puede determinar usando la masa isotópica como se muestra a continuación.
N I-131 = m I-131 . N A / M I-131
N I-131 = (1 μg) x (6.02 × 10 23 núcleos / mol) / (130.91 g / mol)
N I-131 = 4.6 x 10 15 núcleos
- La actividad del yodo-131 en los curies se puede determinar utilizando su constante de descomposición :
El yodo-131 tiene una vida media de 8.02 días (692928 segundos) y, por lo tanto, su constante de descomposición es:
Usando este valor para la constante de desintegración podemos determinar la actividad de la muestra:
3) y 4) El número de átomos de yodo-131 que permanecerán en 50 días (N 50d ) y el tiempo que le tomará a la actividad alcanzar 0.1 mCi puede calcularse usando la ley de descomposición:
Como se puede ver, después de 50 días, el número de átomos de yodo-131 y, por lo tanto, la actividad será aproximadamente 75 veces menor. Después de 82 días, la actividad será aproximadamente 1200 veces menor. Por lo tanto, el tiempo de diez vidas medias (factor 2 10 = 1024) se usa ampliamente para definir la actividad residual.
……………………………………………………………………………………………………………………………….
Este artículo se basa en la traducción automática del artículo original en inglés. Para más información vea el artículo en inglés. Puedes ayudarnos. Si desea corregir la traducción, envíela a: [email protected] o complete el formulario de traducción en línea. Agradecemos su ayuda, actualizaremos la traducción lo antes posible. Gracias.