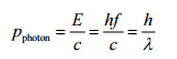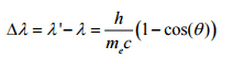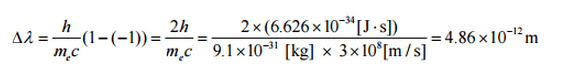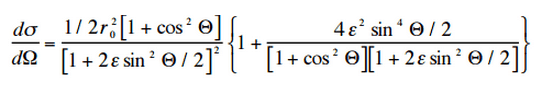Os raios gama , também conhecidos como radiação gama , se referem à radiação eletromagnética (sem massa em repouso, sem carga) de energias muito altas. Os raios gama são fótons de alta energia com comprimentos de onda muito curtos e, portanto, frequência muito alta. Como os raios gama são em substância apenas fótons de alta energia, eles são matéria muito penetrante e, portanto, biologicamente perigosos. Os raios gama podem viajar milhares de pés no ar e podem facilmente passar pelo corpo humano.
Os raios gama são emitidos por núcleos instáveis em sua transição de um estado de alta energia para um estado inferior, conhecido como decaimento gama. Na maioria das fontes práticas de laboratório, os estados nucleares excitados são criados no decaimento de um radionuclídeo pai, portanto, um decaimento gama geralmente acompanha outras formas de decaimento , como decaimento alfa ou beta.
Radiação e também raios gama estão ao nosso redor. Dentro, ao redor e acima do mundo em que vivemos. É uma parte do nosso mundo natural que está aqui desde o nascimento do nosso planeta. As fontes naturais de raios gama na Terra são, entre outros, raios gama de radionuclídeos que ocorrem naturalmente, particularmente o potássio-40. O potássio-40 é um isótopo radioativo de potássio que tem uma meia-vida muito longa de 1.251 × 10 9 anos (comparável à idade da Terra). Este isótopo pode ser encontrado no solo, água também na carne e banana. Este não é o único exemplo de fonte natural de raios gama.
Descoberta de raios gama
Os raios gama foram descobertos logo após a descoberta dos raios X. Em 1896, o cientista francês Henri Becquerel descobriu que os minerais de urânio poderiam expor uma placa fotográfica através de outro material. Becquerel presumiu que o urânio emitisse alguma luz invisível semelhante aos raios X, que foram descobertos recentemente pela WCRoentgen . Ele chamou de ” fosforescência metálica “. De fato, Henri Becquerel descobriu que a radiação gama é emitida pelo radioisótopo 226 Ra (rádio), que faz parte da série Uranium da cadeia de decaimento do urânio.
Primeiro, pensou-se que os raios gama eram partículas com massa, por exemplo, partículas beta extremamente energéticas. Essa opinião falhou, porque essa radiação não pode ser desviada por um campo magnético, o que indicava que eles não tinham carga. Em 1914, observou-se que os raios gama refletiam-se nas superfícies de cristal, provando que deveriam ser radiação eletromagnética , mas com maior energia (maior frequência e comprimentos de onda mais curtos).
Características dos Raios Gama / Radiação
- Os raios gama são fótons de alta energia (cerca de 10.000 vezes mais energia que os fótons visíveis), os mesmos fótons que os fótons que formam a faixa visível do espectro eletromagnético – a luz.
- Fótons (raios gama e raios X) podem ionizar átomos diretamente (apesar de serem eletricamente neutros) através do efeito Fotoelétrico e do efeito Compton, mas a ionização secundária (indireta) é muito mais significativa.
- Os raios gama ionizam a matéria principalmente via ionização indireta .
- Embora seja conhecido um grande número de possíveis interações, existem três mecanismos principais de interação com a matéria.
- Efeito fotoelétrico
- Efeito Compton
- Produção de pares
- Os raios gama viajam na velocidade da luz e podem viajar milhares de metros no ar antes de gastar sua energia.
- Como a radiação gama é uma matéria muito penetrante, ela deve ser protegida por materiais muito densos, como chumbo ou urânio.
- A distinção entre raios X e raios gama não é tão simples e mudou nas últimas décadas. De acordo com a definição atualmente válida, os raios X são emitidos por elétrons fora do núcleo, enquanto os raios gama são emitidos pelo núcleo .
- Os raios gama frequentemente acompanham a emissão de radiação alfa e beta .
Efeito fotoelétrico
- O efeito fotoelétrico domina com baixas energias dos raios gama .
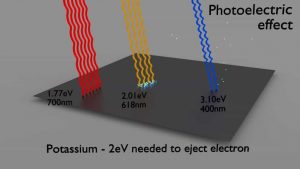
- O efeito fotoelétrico leva à emissão de fotoelétrons da matéria quando a luz ( fótons ) brilha sobre eles.
- A energia máxima que um elétron pode receber em qualquer interação é hν .
- Os elétrons são emitidos apenas pelo efeito fotoelétrico se o fóton atingir ou exceder um limiar de energia .
- Um elétron livre (por exemplo, da nuvem atômica) não pode absorver toda a energia do fóton incidente. Isso é resultado da necessidade de economizar impulso e energia.
- A seção transversal para a emissão de n = 1 fotoelétrons (casca K) é maior que a dos n = 2 fotoelétrons (casca L). Isso é resultado da necessidade de economizar impulso e energia.
Definição de efeito fotoelétrico
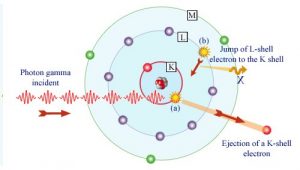
No efeito fotoelétrico, um fóton sofre uma interação com um elétron que está ligado em um átomo. Nesta interação, o fóton incidente desaparece completamente e um fotoelétron energético é ejetado pelo átomo de uma de suas conchas ligadas . A energia cinética do fotoelétron ejetado (E e ) é igual à energia incidente do fóton (hν) menos a energia de ligação do fotoelétron em seu invólucro original (E b ).
E e = hν-E b
Portanto, os fotoelétrons são emitidos apenas pelo efeito fotoelétrico se o fóton atingir ou exceder um limiar de energia – a energia de ligação do elétron – a função de trabalho do material. Para raios gama com energias superiores a centenas de keV, o fotoelétron retira a maior parte da energia incidente do fóton – hν.
Após uma interação fotoelétrica, um átomo absorvedor ionizado é criado com uma vaga em uma de suas conchas ligadas . Essa vaga será rapidamente preenchida por um elétron de uma concha com uma energia de ligação mais baixa (outras conchas) ou pela captura de um elétron livre do material. O rearranjo de elétrons de outras camadas cria outra vaga que, por sua vez, é preenchida por um elétron de uma camada de energia de ligação ainda mais baixa. Portanto, uma cascata de raios-X mais característicos também pode ser gerada. A probabilidade de emissão característica de raios-X diminui à medida que o número atômico do absorvedor diminui. Às vezes, a emissão de um elétron Auger ocorre.
Seções Cruzadas de Efeito Fotoelétrico
Em pequenos valores de energia de raios gama, o efeito fotoelétrico domina . O mecanismo também é aprimorado para materiais de alto número atômico Z. Não é simples derivar expressão analítica para a probabilidade de absorção fotoelétrica de raios gama por átomo em todas as faixas de energias de raios gama. A probabilidade de absorção fotoelétrica por unidade de massa é aproximadamente proporcional a:
τ (fotoelétrico) = constante x Z N / E 3.5
onde Z é o número atômico, o expoente n varia entre 4 e 5. E é a energia do fóton incidente. A proporcionalidade para potências mais altas do número atômico Z é a principal razão para o uso de materiais com alto teor de Z, como chumbo ou urânio empobrecido em escudos de raios gama.
Embora a probabilidade de absorção fotoelétrica do fóton gama diminua, em geral, com o aumento da energia do fóton, existem acentuadas descontinuidades na curva de seção transversal. Estes são chamados de “bordas de absoption”e eles correspondem às energias de ligação dos elétrons das conchas atadas dos átomos. Para fótons com a energia logo acima da borda, a energia do fóton é apenas suficiente para sofrer a interação fotoelétrica com o elétron da casca ligada, digamos K-shell. A probabilidade de tal interação está logo acima dessa borda muito maior do que a de fótons de energia ligeiramente abaixo dessa borda. Para os fótons gama abaixo dessa borda, a interação com o elétron da casca K é energeticamente impossível e, portanto, a probabilidade cai abruptamente. Essas arestas ocorrem também em energias de ligação de elétrons de outras camadas (L, M, N … ..).
Efeito Compton
Principais características do Compton Scattering
- A dispersão de Compton domina em energias intermediárias.
- É a dispersão de fótons por elétrons atômicos
- Os fótons passam por um deslocamento de comprimento de onda chamado deslocamento de Compton.
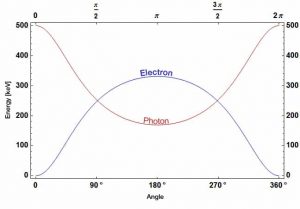
- A energia transferida para o elétron de recuo pode variar de zero a uma grande fração da energia incidente de raios gama
Definição de dispersão de Compton
A dispersão de Compton é a dispersão inelástica ou não clássica de um fóton (que pode ser um fóton de raios X ou gama ) por uma partícula carregada, geralmente um elétron. Na dispersão de Compton, o fóton de raios gama incidente é desviado através de um ângulo Θ em relação à sua direção original. Essa deflexão resulta em uma diminuição na energia (diminuição na frequência do fóton) do fóton e é chamado de efeito Compton . O fóton transfere uma parte de sua energia para o elétron de recuo . A energia transferida para o elétron de recuo pode variar de zero a uma grande fração da energia incidente de raios gama, porque todos os ângulos de dispersão são possíveis. A dispersão de Compton foi observada por AHCompton em 1923na Universidade de Washington em St. Louis. Compton ganhou o Prêmio Nobel de Física em 1927 por esse novo entendimento sobre a natureza das partículas dos fótons.
Fórmula de dispersão de Compton
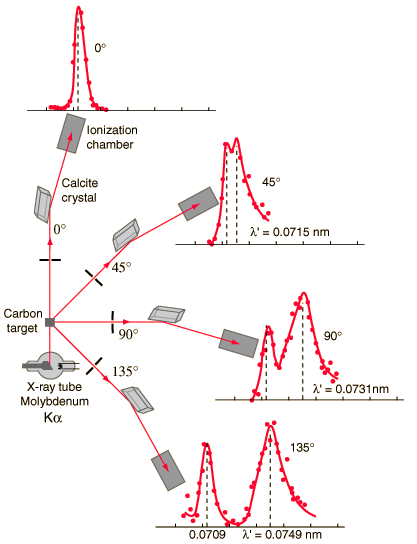
A fórmula de Compton foi publicada em 1923 na Physical Review. Compton explicou que o deslocamento dos raios X é causado pelo momento de partículas dos fótons. A fórmula de dispersão de Compton é a relação matemática entre a mudança no comprimento de onda e o ângulo de dispersão dos raios-X. No caso de espalhamento de Compton, o fóton de frequência f colide com um elétron em repouso. Após a colisão, o fóton ricocheteia o elétron, liberando parte de sua energia inicial (dada pela fórmula E = hf de Planck). Enquanto o elétron ganha impulso (massa x velocidade), o fóton não pode diminuir sua velocidade . Como resultado da lei de conservação do momento, o fóton deve diminuir seu momento dado por:
Portanto, a diminuição do momento do fóton deve ser traduzida em diminuição da frequência (aumento no comprimento de onda Δ λ = λ ‘- λ ). A mudança do comprimento de onda aumentou com o ângulo de dispersão de acordo com a fórmula de Compton :
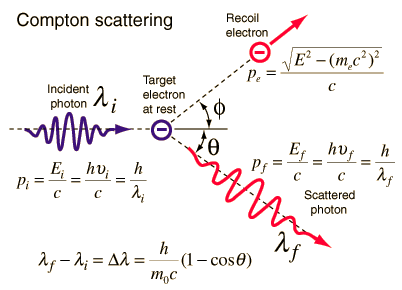
Fonte: hyperphysics.phy-astr.gsu.edu
Onde
λ é o comprimento de onda inicial do fóton
λ ‘ é o comprimento de onda após a dispersão,
h é a constante de Planck = 6,626 x 10 -34 Js
m e é a massa de repouso do elétron (0,511 MeV)
c é a velocidade da luz
Θ é o ângulo de dispersão.
A mudança mínima no comprimento de onda ( λ ′ – λ ) para o fóton ocorre quando Θ = 0 ° (cos (Θ) = 1) e é pelo menos zero. A variação máxima no comprimento de onda ( λ ′ – λ ) para o fóton ocorre quando Θ = 180 ° (cos (Θ) = – 1). Neste caso, o fóton transfere para o elétron o máximo de momento possível. A variação máxima no comprimento de onda pode ser derivada da fórmula de Compton:
A quantidade h / m e c é conhecida como comprimento de onda do elétron de Compton e é igual a 2,43 × 10 −12 m .
Dispersão de Compton – seções transversais
A probabilidade de espalhamento de Compton por interação com um átomo aumenta linearmente com o número atômico Z, porque depende do número de elétrons disponíveis para espalhamento no átomo alvo. A distribuição angular de fótons dispersos a partir de um único elétron livre é descrita pela fórmula de Klein-Nishina :
onde ε = E 0 / m e c 2 e r 0 é o “raio clássico do elétron” igual a cerca de 2,8 x 10 -13 cm. A fórmula fornece a probabilidade de espalhar um fóton no elemento de ângulo sólido dΩ = 2π sin Θ dΘ quando a energia incidente é E 0 .
Fonte: hyperphysics.phy-astr.gsu.edu/
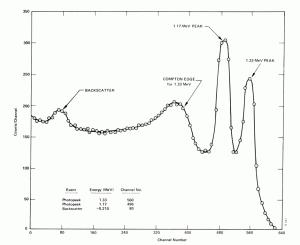
Compton Edge
Na espectrofotometria, a borda de Compton é uma característica do espectrógrafo que resulta da dispersão de Compton no cintilador ou detector. Esse recurso é devido aos fótons que sofrem dispersão de Compton com um ângulo de dispersão de 180 ° e escapam do detector. Quando um raio gama se espalha pelo detector e escapa, apenas uma fração de sua energia inicial pode ser depositada na camada sensível do detector. Depende do ângulo de dispersão do fóton, quanta energia será depositada no detector. Isso leva a um espectro de energias. A energia da borda de Compton corresponde ao fóton retroespalhado total .
Dispersão inversa de Compton
A dispersão inversa de Compton é a dispersão de fótons de baixa energia para altas energias por elétrons relativísticos. Os elétrons relativísticos podem aumentar a energia dos fótons de baixa energia em uma quantidade potencialmente enorme (até raios gama podem ser produzidos). Este fenômeno é muito importante na astrofísica.
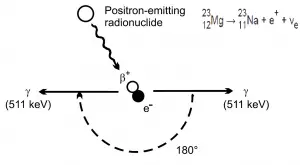
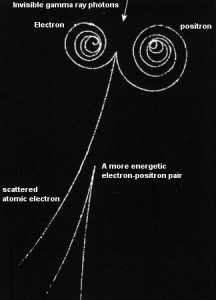
Produção de Par Positron-Elétron
Se a energia do fóton original for maior que 1,02MeV, qualquer energia acima de 1,02MeV estará de acordo com a lei de conservação dividida entre a energia cinética de movimento das duas partículas.
A presença de um campo elétrico de um átomo pesado , como chumbo ou urânio, é essencial para satisfazer a conservação do momento e da energia . A fim de satisfazer a conservação do momento e da energia, o núcleo atômico deve receber algum momento. Portanto, uma produção de par de fótons no espaço livre não pode ocorrer .
Além disso, o pósitron é a antipartícula do elétron; portanto, quando um pósitron pára, ele interage com outro elétron, resultando na aniquilação de ambas as partículas e na conversão completa de sua massa de repouso em energia pura (de acordo com o E = mc 2 fórmula) na forma de dois sentidos opostos 0,511 MeV raios gama (fotões). O fenômeno da produção de pares está, portanto, conectado à criação e destruição da matéria em uma única reação.
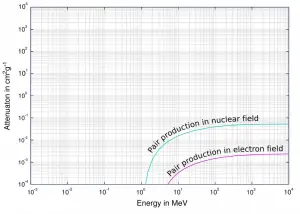
Produção de Par Positron-Elétron – Seção Transversal
A probabilidade de produção de pares, caracterizada pela seção transversal, é uma função muito complicada baseada na mecânica quântica . Em geral, a seção transversal aumenta aproximadamente com o quadrado do número atômico (σ p ~ Z 2 ) e aumenta com a energia do fóton, mas essa dependência é muito mais complexa.
Atenuação de raios gama
A seção transversal total da interação de raios gama com um átomo é igual à soma das três seções parciais mencionadas:
σ = σ f + σ C + σ p
- σ f – Efeito fotoelétrico
- σ C – espalhamento de Compton
- σ p – Produção em pares
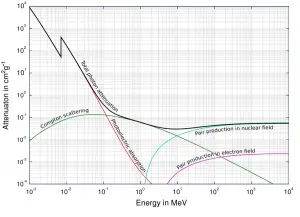
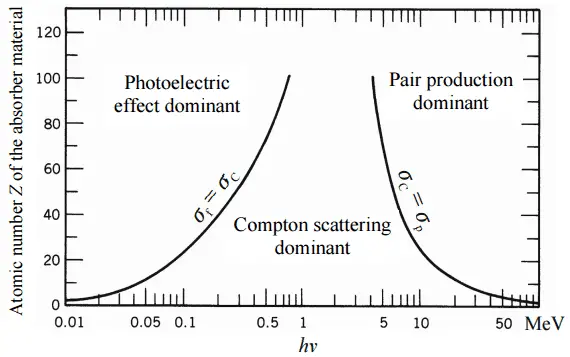
Dependendo da energia dos raios gama e do material absorvedor, uma das três seções parciais pode se tornar muito maior que as outras duas. Em pequenos valores de energia de raios gama, o efeito fotoelétrico domina. A dispersão de Compton domina em energias intermediárias. A dispersão de comptons também aumenta com a diminuição do número atômico de matéria; portanto, o intervalo de dominação é maior para os núcleos leves. Finalmente, a produção de pares elétron-pósitron domina com altas energias.
Com base na definição de seção transversal de interação, pode-se derivar a dependência da intensidade dos raios gama na espessura do material absorvente. Se os raios gama monoenergéticos forem colimados em um feixe estreito e se o detector atrás do material detectar apenas os raios gama que passaram por esse material sem nenhum tipo de interação com esse material, a dependência deverá ser uma atenuação exponencial simples dos raios gama . Cada uma dessas interações remove o fóton do feixe por absorção ou dispersão na direção do detector. Portanto, as interações podem ser caracterizadas por uma probabilidade fixa de ocorrência por unidade de comprimento do caminho no absorvedor. A soma dessas probabilidades é chamada decoeficiente de atenuação linear :
μ = τ (fotoelétrico) + σ (Compton) + κ (par)
Coeficiente de atenuação linear
A atenuação da radiação gama pode ser então descrita pela seguinte equação.
I = I 0 .e -μx
, onde I é a intensidade após a atenuação, I o é a intensidade do incidente, μ é o coeficiente de atenuação linear (cm -1 ) e a espessura física do absorvedor (cm).
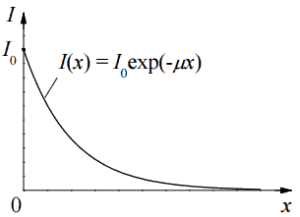
Os materiais listados na tabela ao lado são ar, água e elementos diferentes do carbono ( Z = 6) ao chumbo ( Z = 82) e seus coeficientes de atenuação linear são dados para três energias de raios gama. Existem duas características principais do coeficiente de atenuação linear:
- O coeficiente de atenuação linear aumenta à medida que o número atômico do absorvedor aumenta.
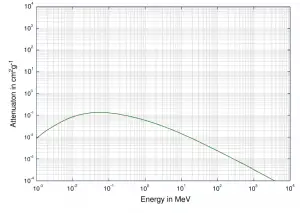
- O coeficiente de atenuação linear para todos os materiais diminui com a energia dos raios gama.
Camada de metade do valor
A camada de meio valor expressa a espessura do material absorvente necessário para reduzir a intensidade da radiação incidente por um fator de dois . Existem duas características principais da camada de meio valor:
- A camada de metade do valor diminui à medida que o número atômico do absorvedor aumenta. Por exemplo, são necessários 35 m de ar para reduzir a intensidade de um feixe de raios gama de 100 keV por um fator de dois, enquanto apenas 0,12 mm de chumbo podem fazer a mesma coisa.
- A camada de metade do valor para todos os materiais aumenta com a energia dos raios gama. Por exemplo, de 0,26 cm para ferro a 100 keV a cerca de 1,06 cm a 500 keV.
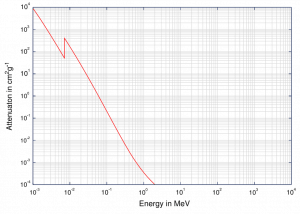
Coeficiente de atenuação de massa
Ao caracterizar um material absorvente, às vezes podemos usar o coeficiente de atenuação da massa. O coeficiente de atenuação da massa é definido como a razão entre o coeficiente de atenuação linear e a densidade do absorvedor (μ / ρ) . A atenuação da radiação gama pode ser descrita pela seguinte equação:
I = I 0 .e – (μ / ρ) .ρl
, onde ρ é a densidade do material, (μ / ρ) é o coeficiente de atenuação da massa e ρ.l é a espessura da massa. A unidade de medida usada para o coeficiente de atenuação da massa cm 2 g -1 .
Para energias intermediárias, o espalhamento de Compton domina e diferentes absorvedores têm coeficientes de atenuação de massa aproximadamente iguais. Isso se deve ao fato de que a seção transversal da dispersão de Compton é proporcional ao Z (número atômico) e, portanto, o coeficiente é proporcional à densidade do material ρ. Em pequenos valores de energia de raios gama ou em altos valores de energia de raios gama, em que o coeficiente é proporcional a potências mais altas do número atômico Z (para efeito fotoelétrico σ f ~ Z 5 ; para produção de pares σ p ~ Z 2 ), o o coeficiente de atenuação μ não é uma constante.
Exemplo:
De quanto água você precisa, se você deseja reduzir a intensidade de um feixe de raios gama monoenergético de 500 keV ( feixe estreito ) para 1% de sua intensidade incidente? A camada de meio valor para raios gama de 500 keV na água é de 7,15 cm e o coeficiente de atenuação linear para raios gama de 500 keV na água é de 0,097 cm -1 .
A questão é bastante simples e pode ser descrita pela seguinte equação:
Se a camada de meio valor para a água for 7,15 cm, o coeficiente de atenuação linear é:
Agora podemos usar a equação de atenuação exponencial:
Portanto
Portanto, a espessura necessária da água é de cerca de 47,5 cm . Essa espessura é relativamente grande e é causada por um pequeno número atômico de hidrogênio e oxigênio. Se calcularmos o mesmo problema para o chumbo (Pb) , obteremos a espessura x = 2,8 cm .
Coeficientes de atenuação linear
Tabela de coeficientes de atenuação linear (em cm-1) para diferentes materiais com energias de raios gama de 100, 200 e 500 keV.
| Absorvedor | 100 keV | 200 keV | 500 keV |
| Ar | 0.000195 / cm | 0.000159 / cm | 0.000112 / cm |
| Água | 0,167 / cm | 0,136 / cm | 0,097 / cm |
| Carbono | 0,335 / cm | 0,274 / cm | 0.196 / cm |
| Alumínio | 0.435 / cm | 0,324 / cm | 0,227 / cm |
| Ferro | 2,72 / cm | 1.09 / cm | 0.655 / cm |
| Cobre | 3.8 / cm | 1,309 / cm | 0,73 / cm |
| Conduzir | 59,7 / cm | 10,15 / cm | 1,64 / cm |
Camadas de metade do valor
Tabela de camadas de meio valor (em cm) para diferentes materiais com energias de raios gama de 100, 200 e 500 keV.
| Absorvedor | 100 keV | 200 keV | 500 keV |
| Ar | 3555 cm | 4359 cm | 6189 cm |
| Água | 4,15 cm | 5.1 cm | 7.15 cm |
| Carbono | 2,07 cm | 2,53 cm | 3.54 cm |
| Alumínio | 1,59 cm | 2,14 cm | 3.05 cm |
| Ferro | 0,26 cm | 0,64 cm | 1.06 cm |
| Cobre | 0,18 cm | 0,53 cm | 0,95 cm |
| Conduzir | 0.012 cm | 0.068 cm | 0,42 cm |
Validade da lei exponencial
A lei exponencial sempre descreverá a atenuação da radiação primária pela matéria. Se partículas secundárias forem produzidas
ou se a radiação primária mudar sua energia ou direção, a atenuação efetiva será muito menor. A radiação penetrará mais profundamente na matéria do que a
prevista pela lei exponencial. O processo deve ser levado em consideração ao
avaliar o efeito da proteção contra radiação.
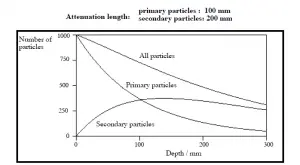
Fatores de acúmulo para blindagem de raios gama
O fator de acumulação é um fator de correção que considera a influência da radiação dispersa mais quaisquer partículas secundárias no meio durante os cálculos de blindagem. Se queremos dar conta do acúmulo de radiação secundária, precisamos incluir o fator de acúmulo . O fator de acumulação é então um fator multiplicativo que responde pela resposta aos fótons não colididos, de modo a incluir a contribuição dos fótons dispersos. Assim, o fator de acumulação pode ser obtido como uma razão entre a dose total e a resposta para a dose não coletada.
A fórmula estendida para o cálculo da taxa de dose é:
O padrão ANSI / ANS-6.4.3-1991 de coeficientes de atenuação de raios gama e fatores de acúmulo para materiais de engenharia contém coeficientes de atenuação de raios gama derivados e fatores de acúmulo para materiais e elementos de engenharia selecionados para uso em cálculos de blindagem (ANSI / ANS-6.1 .1, 1991).
……………………………………………………………………………………………………………………………….
Este artigo é baseado na tradução automática do artigo original em inglês. Para mais informações, consulte o artigo em inglês. Você pode nos ajudar. Se você deseja corrigir a tradução, envie-a para: [email protected] ou preencha o formulário de tradução on-line. Agradecemos sua ajuda, atualizaremos a tradução o mais rápido possível. Obrigado.