Os raios X , também conhecidos como radiação X , referem-se à radiação eletromagnética (sem massa em repouso, sem carga) de altas energias. Os raios X são fótons de alta energia, com comprimentos de onda curtos e, portanto, frequência muito alta. A frequência de radiação é o parâmetro chave de todos os fótons, porque determina a energia de um fóton. Os fótons são classificados de acordo com as energias das ondas de rádio de baixa energia e radiação infravermelha, através da luz visível, aos raios X de alta energia e raios gama .
A maioria dos raios X tem um comprimento de onda variando de 0,01 a 10 nanômetros (3 × 10 16 Hz a 3 × 10 19 Hz), correspondendo a energias na faixa de 100 eV a 100 keV. Os comprimentos de onda dos raios X são mais curtos que os dos raios UV e geralmente mais longos que os dos raios gama. A distinção entre raios X e raios gama não é tão simples e mudou nas últimas décadas. De acordo com a definição atualmente válida, os raios X são emitidos por elétrons fora do núcleo, enquanto os raios gama são emitidos pelo núcleo .
Atenuação de raios X
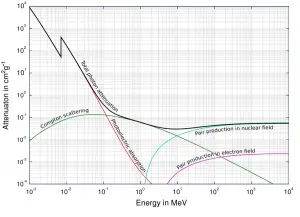
Fonte: Wikimedia Commons
À medida que os fótons de alta energia passam pelo material, sua energia está diminuindo. Isso é conhecido como atenuação . A teoria da atenuação também é válida para raios-X e raios gama . Acontece que os fótons de energia mais alta (raios-X duros) viajam através do tecido mais facilmente do que os fótons de baixa energia (isto é, os fótons de energia mais alta têm menor probabilidade de interagir com a matéria). Grande parte desse efeito está relacionada ao efeito fotoelétrico . A probabilidade de absorção fotoelétrica é aproximadamente proporcional a (Z / E) 3, onde Z é o número atômico do átomo de tecido e E é a energia do fóton. À medida que E aumenta, a probabilidade de interação diminui rapidamente. Para energias mais altas, a dispersão de Compton se torna dominante. A dispersão de Compton é constante para energias diferentes, embora diminua lentamente em energias mais altas.
Atenuação Exponencial
Suponha que os raios X monoenergéticos sejam colimados em um feixe estreito e o detector atrás do material apenas detecte os raios X que passaram por esse material sem nenhum tipo de interação com esse material; então, a dependência deve ser uma atenuação exponencial simples dos raios X . Cada uma dessas interações remove o fóton do feixe por absorção ou dispersão na direção do detector. Portanto, as interações podem ser caracterizadas por uma probabilidade fixa de ocorrência por unidade de comprimento do caminho no absorvedor. A soma dessas probabilidades é chamada de coeficiente de atenuação linear :
μ = τ (fotoelétrico) + σ (Compton)
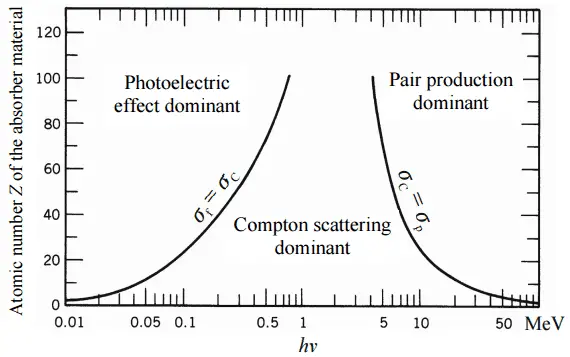
Coeficiente de atenuação linear – raios-X
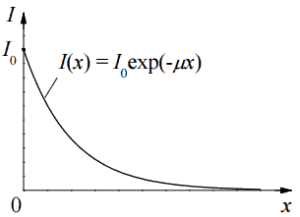
A atenuação dos raios X pode ser descrita pela seguinte equação.
I = I 0 .e -μx
, onde I é a intensidade após a atenuação, I o é a intensidade do incidente, μ é o coeficiente de atenuação linear (cm -1 ) e a espessura física do absorvedor (cm).
Os materiais listados na tabela são ar, água e elementos diferentes do carbono ( Z = 6) ao chumbo ( Z = 82) e seus coeficientes de atenuação linear são dados para duas energias de raios-X. Existem duas características principais do coeficiente de atenuação linear:
- O coeficiente de atenuação linear aumenta à medida que o número atômico do absorvedor aumenta.
- O coeficiente de atenuação linear para todos os materiais diminui com a energia dos raios-X.
Camada de metade do valor
A camada de meio valor expressa a espessura do material absorvente necessário para reduzir a intensidade da radiação incidente por um fator de dois . Existem duas características principais da camada de meio valor:
- A camada de metade do valor diminui à medida que o número atômico do absorvedor aumenta. Por exemplo, são necessários 35 m de ar para reduzir a intensidade de um feixe de raios X de 100 keV por um fator de dois, enquanto apenas 0,12 mm de chumbo podem fazer a mesma coisa.
- A camada de metade do valor para todos os materiais aumenta com a energia dos raios-X. Por exemplo, de 0,26 cm para ferro a 100 keV a cerca de 0,64 cm a 200 keV.
Coeficiente de atenuação de massa
Ao caracterizar um material absorvente, às vezes podemos usar o coeficiente de atenuação da massa. O coeficiente de atenuação da massa é definido como a razão entre o coeficiente de atenuação linear e a densidade do absorvedor (μ / ρ) . A atenuação dos raios X pode ser descrita pela seguinte equação:
I = I 0 .e – (μ / ρ) .ρl
, onde ρ é a densidade do material, (μ / ρ) é o coeficiente de atenuação da massa e ρ.l é a espessura da massa. A unidade de medida usada para o coeficiente de atenuação da massa cm 2 g -1 . Para energias intermediárias, o espalhamento de Compton domina e diferentes absorvedores têm coeficientes de atenuação de massa aproximadamente iguais . Isso se deve ao fato de que a seção transversal da dispersão de Compton é proporcional ao Z (número atômico) e, portanto, o coeficiente é proporcional à densidade do material ρ. Em pequenos valores de energia de raios-X, onde o coeficiente é proporcional a potências mais altas do número atômico Z (para efeito fotoelétrico σ f ~ Z 3 ), o coeficiente de atenuação μ não é constante.
Veja também calculadora: Atividade gama para taxa de dose (com / sem proteção)
Consulte também XCOM – seção transversal do fóton DB: XCOM: banco de dados de seções transversais do fóton
Exemplo:
De quanto água é necessário o escorço, se você deseja reduzir a intensidade de um feixe de raios X monoenergético de 100 keV ( feixe estreito ) para 1% da intensidade do incidente? A camada de meio valor para raios-X de 100 keV na água é de 4,15 cm e o coeficiente de atenuação linear para raios-X de 100 keV na água é de 0,167 cm- 1 . O problema é bastante simples e pode ser descrito pela seguinte equação:
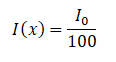 Se a camada de meio valor para a água for 4,15 cm, o coeficiente de atenuação linear é:
Se a camada de meio valor para a água for 4,15 cm, o coeficiente de atenuação linear é: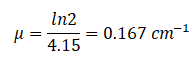 Agora podemos usar a equação de atenuação exponencial:
Agora podemos usar a equação de atenuação exponencial: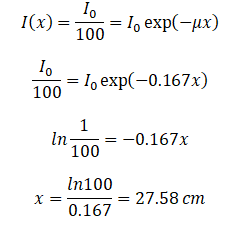
Portanto, a espessura necessária da água é de cerca de 27,58 cm . Essa espessura é relativamente grande e é causada por um pequeno número atômico de hidrogênio e oxigênio. Se calcularmos o mesmo problema para o chumbo (Pb) , obteremos a espessura x = 0,077 cm .
Coeficientes de atenuação linear
Tabela de coeficientes de atenuação linear (em cm -1 ) para diferentes materiais com energias de fótons de 100, 200 e 500 keV.
| Absorvedor | 100 keV | 200 keV | 500 keV |
| Ar | 0.000195 / cm | 0.000159 / cm | 0.000112 / cm |
| Água | 0,167 / cm | 0,136 / cm | 0,097 / cm |
| Carbono | 0,335 / cm | 0,274 / cm | 0.196 / cm |
| Alumínio | 0.435 / cm | 0,324 / cm | 0,227 / cm |
| Ferro | 2,72 / cm | 1.09 / cm | 0.655 / cm |
| Cobre | 3.8 / cm | 1,309 / cm | 0,73 / cm |
| Conduzir | 59,7 / cm | 10,15 / cm | 1,64 / cm |
Camadas de metade do valor
Tabela de camadas de meio valor (em cm) para diferentes materiais com energias de fótons de 100, 200 e 500 keV.
| Absorvedor | 100 keV | 200 keV | 500 keV |
| Ar | 3555 cm | 4359 cm | 6189 cm |
| Água | 4,15 cm | 5.1 cm | 7.15 cm |
| Carbono | 2,07 cm | 2,53 cm | 3.54 cm |
| Alumínio | 1,59 cm | 2,14 cm | 3.05 cm |
| Ferro | 0,26 cm | 0,64 cm | 1.06 cm |
| Cobre | 0,18 cm | 0,53 cm | 0,95 cm |
| Conduzir | 0.012 cm | 0.068 cm | 0,42 cm |
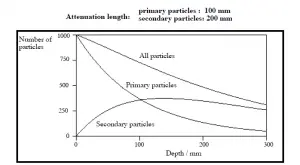
Validade da lei exponencial
A lei exponencial sempre descreverá a atenuação da radiação primária pela matéria. Se partículas secundárias forem produzidas ou se a radiação primária mudar sua energia ou direção, a atenuação efetiva será muito menor. A radiação penetrará mais profundamente na matéria do que a prevista pela lei exponencial. O processo deve ser levado em consideração ao avaliar o efeito da proteção contra radiação.
……………………………………………………………………………………………………………………………….
Este artigo é baseado na tradução automática do artigo original em inglês. Para mais informações, consulte o artigo em inglês. Você pode nos ajudar. Se você deseja corrigir a tradução, envie-a para: [email protected] ou preencha o formulário de tradução on-line. Agradecemos sua ajuda, atualizaremos a tradução o mais rápido possível. Obrigado.