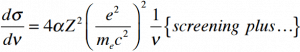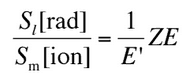Descripción Partículas Beta
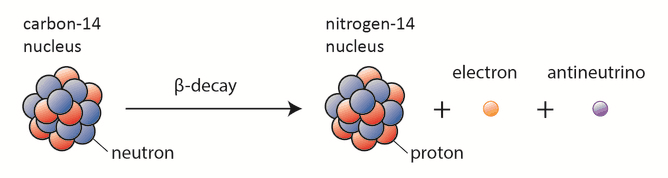
Las partículas beta son electrones o positrones de alta energía y alta velocidad emitidos por ciertos fragmentos de fisión o por ciertos núcleos radiactivos primordiales como el potasio-40. Las partículas beta son una forma de radiación ionizante también conocida como rayos beta. La producción de partículas beta se denomina desintegración beta . Hay dos formas de desintegración beta, la desintegración de electrones (desintegración β) y la desintegración de positrones (desintegración β +) . En un reactor nuclear ocurre especialmente la desintegración β, porque la característica común de los productos de fisión es un exceso de neutrones ( ver Estabilidad nuclear).) Un fragmento de fisión inestable con el exceso de neutrones sufre desintegración β, donde el neutrón se convierte en un protón, un electrón y un antineutrino electrónico .
Espectro de partículas beta
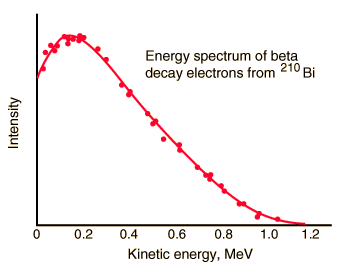
En el proceso de desintegración beta, se emite un electrón o un positrón. Esta emisión se acompaña de la emisión de antineutrino (desintegración β) o neutrino (desintegración β +), que comparte la energía y el impulso de la desintegración. La emisión beta tiene un espectro característico. Este espectro característico es causado por el hecho de que se emite un neutrino o un antineutrino con emisión de partículas beta. La forma de esta curva de energía depende de qué fracción de la energía de reacción ( valor Q -la cantidad de energía liberada por la reacción) es transportada por la partícula masiva. Por lo tanto, las partículas beta pueden ser emitidos con cualquier energía cinética que van desde 0 a Q . Para 1934, Enrico Fermi había desarrollado unLa teoría de Fermi de la desintegración beta , que predijo la forma de esta curva de energía.
Naturaleza de la interacción de la radiación beta con la materia
Resumen de tipos de interacciones:
- Colisiones inelásticas con electrones atómicos (excitación e ionización)
- Dispersión elástica de núcleos
- Bremsstrahlung.
- Radiación de Cherenkov.
- Aniquilación (solo positrones)

La naturaleza de la interacción de una radiación beta con la materia es diferente de la radiación alfa , a pesar de que las partículas beta también son partículas cargadas. En comparación con las partículas alfa, las partículas beta tienen una masa mucho menor y alcanzan principalmente energías relativistas . Su masa es igual a la masa de los electrones orbitales con los que están interactuando y, a diferencia de la partícula alfa, una fracción mucho mayor de su energía cinética se puede perder en una sola interacción. Dado que las partículas beta alcanzan principalmente energías relativistas, la fórmula Bethe no relativista no se puede utilizar. Para electrones de alta energía, Bethe también ha derivado una expresión similarpara describir la pérdida de energía específica debido a la excitación e ionización (las «pérdidas por colisión»).
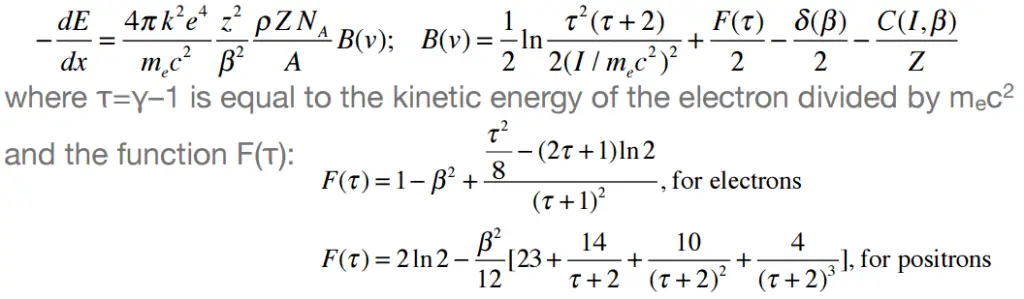
Además, las partículas beta pueden interactuar a través de la interacción electrón-nuclear (dispersión elástica de los núcleos), lo que puede cambiar significativamente la dirección de la partícula beta . Por lo tanto, su camino no es tan sencillo. Las partículas beta siguen una ruta muy en zig-zag a través del material absorbente, esta ruta resultante de partículas es más larga que la penetración lineal (rango) en el material.
Las partículas beta también difieren de otras partículas cargadas pesadas en la fracción de energía perdida por el proceso radiativo conocido como bremsstrahlung . Según la teoría clásica, cuando una partícula cargada se acelera o desacelera, debe irradiar energía y la radiación de desaceleración se conoce como bremsstrahlung («radiación de frenado») .
Existe otro mecanismo por el cual las partículas beta pierden energía a través de la producción de radiación electromagnética. Cuando la partícula beta se mueve más rápido que la velocidad de la luz (velocidad de fase) en el material, genera una onda de choque de radiación electromagnética conocida como radiación de Cherenkov .
Los positrones interactúan de manera similar con la materia cuando son energéticos . Pero cuando el positrón se detiene , interactúa con un electrón cargado negativamente, lo que resulta en la aniquilación del par electrón-positrón.
Bremsstrahlung
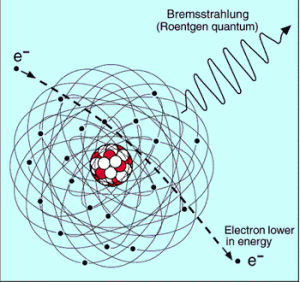
El bremsstrahlung es radiación electromagnética producida por la aceleración o desaceleración de una partícula cargada cuando es desviada por campos magnéticos (un electrón por campo magnético del acelerador de partículas) u otra partícula cargada (un electrón por un núcleo atómico). El nombre bremsstrahlung proviene del alemán. La traducción literal es ‘radiación de frenado’ . Según la teoría clásica, cuando una partícula cargada se acelera o desacelera, debe irradiar energía.
El bremsstrahlung es una de las posibles interacciones de partículas cargadas de luz con la materia (especialmente con altos números atómicos ).
Los dos casos más comunes de bremsstrahlung son:
- Desaceleración de partículas cargadas. Cuando las partículas cargadas entran en un material, son desaceleradas por el campo eléctrico de los núcleos atómicos y los electrones atómicos.
- Aceleración de partículas cargadas. Cuando las partículas cargadas ultra-relativistas se mueven a través de campos magnéticos, se ven obligadas a moverse a lo largo de una trayectoria curva. Dado que su dirección de movimiento cambia continuamente, también están acelerando y emiten bremsstrahlung, en este caso se denomina radiación sincrotrón .
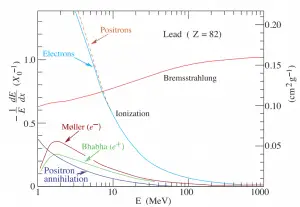
función de la energía de electrones o positrones. Fuente: http://pdg.lbl.gov/
Dado que el bremsstrahlung es mucho más fuerte para las partículas más ligeras, este efecto es mucho más importante para las partículas beta que para los protones, las partículas alfa y los núcleos pesados ( fragmentos de fisión ). Este efecto puede descuidarse con energías de partículas por debajo de aproximadamente 1 MeV , porque la pérdida de energía debido a bremsstrahlung es muy pequeña. La pérdida de radiación comienza a ser importante solo a energías de partículas muy por encima de la energía mínima de ionización. En las energías relativistas, la relación entre la tasa de pérdida por bremsstrahlung y la tasa de pérdida por ionización es aproximadamente proporcional al producto de la energía cinética de la partícula y al número atómico del absorbedor.
La sección transversal de bremsstrahlung depende principalmente de estos términos:
Entonces, la proporción de poderes de frenado de bremsstrahlung y pérdidas de ionización es:
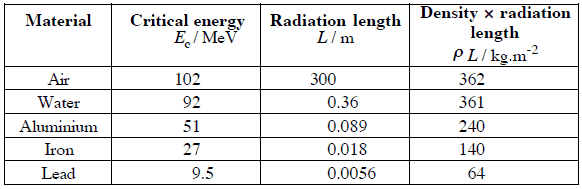
, donde E es la energía cinética de la partícula (electrón), Z es el número atómico medio del material y E ‘es una constante de proporcionalidad; E ‘≈ 800 MeV . La energía cinética a la cual la pérdida de energía por bremsstrahlung es igual a la pérdida de energía por ionización y excitación (pérdidas por colisión) se denomina energía crítica . Otro paremeter es la longitud de radiación , definida como la distancia sobre la cual la energía del electrón incidente se reduce en un factor 1 / e (0.37) debido a las pérdidas de radiación solamente. La siguiente tabla proporciona algunos valores típicos:
Radiación Cherenkov
La radiación cherenkov es radiación electromagnética emitida cuando una partícula cargada (como un electrón) se mueve a través de un medio dieléctrico más rápido que la velocidad de fase de la luz en ese medio . Es similar a la onda de proa producida por un barco que viaja más rápido que la velocidad de las ondas de agua. La radiación de Cherenkov se produce solo si la velocidad de la partícula es mayor que la velocidad de fase de la luz en el material. Incluso a altas energías, la energía perdida por la radiación de Cherenkov es mucho menor que la de los otros mecanismos (colisiones, bremsstrahlung). Lleva el nombre del físico soviético Pavel Alekseyevich Cherenkov , quien compartió el Premio Nobel de física en 1958 conIlya Frank e Igor Tamm por el descubrimiento de la radiación Cherenkov, realizada en 1934.


La radiación de Cherenkov se puede usar para detectar partículas cargadas de alta energía (especialmente partículas beta). En los reactores nucleares o en un grupo de combustible nuclear gastado, las partículas beta (electrones de alta energía) se liberan a medida que se descomponen los fragmentos de fisión. El brillo también es visible después de que la reacción en cadena se detiene (en el reactor). La radiación cherenkov puede caracterizar la radiactividad restante del combustible nuclear gastado, por lo tanto, se puede utilizar para medir el consumo de combustible.
Interacciones de positrones
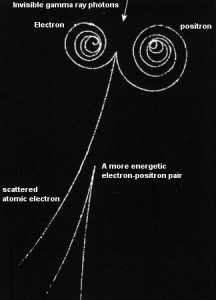 Las fuerzas de coulomb que constituyen el mecanismo principal de pérdida de energía para los electrones están presentes para la carga positiva o negativa en la partícula y constituyen el mecanismo principal de pérdida de energía también para los positrones. Cualquiera que sea la interacción implica una fuerza repulsiva o atractiva entre la partícula incidente y el electrón orbital (o núcleo atómico), el impulso y la transferencia de energía para partículas de igual masa son casi iguales . Por lo tanto, los positrones interactúan de manera similar con la materia cuando son energéticos . La pista de positrones en el material es similar a la pista de electrones. Incluso su pérdida y rango de energía específicos son casi iguales para energías iniciales iguales.
Las fuerzas de coulomb que constituyen el mecanismo principal de pérdida de energía para los electrones están presentes para la carga positiva o negativa en la partícula y constituyen el mecanismo principal de pérdida de energía también para los positrones. Cualquiera que sea la interacción implica una fuerza repulsiva o atractiva entre la partícula incidente y el electrón orbital (o núcleo atómico), el impulso y la transferencia de energía para partículas de igual masa son casi iguales . Por lo tanto, los positrones interactúan de manera similar con la materia cuando son energéticos . La pista de positrones en el material es similar a la pista de electrones. Incluso su pérdida y rango de energía específicos son casi iguales para energías iniciales iguales.
Al final de su camino , los positrones difieren significativamente de los electrones. Cuando un positrón (partícula antimateria) se detiene, interactúa con un electrón (partícula de materia), lo que resulta en la aniquilación de ambas partículas y la conversión completa de su masa en reposo en energía pura (de acuerdo con la fórmula E = mc 2 ) en forma de dos rayos gamma ( fotones ) de 0.511 MeV opuestos .
Aniquilación de positrones
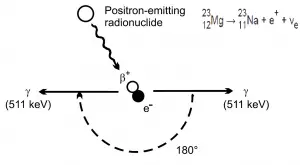
La aniquilación de electrones-positrones ocurre cuando un electrón con carga negativa y un positrón con carga positiva chocan. Cuando un electrón de baja energía aniquila un positrón de baja energía (antipartícula de electrones), solo pueden producir dos o más fotones (rayos gamma). La producción de un solo fotón está prohibida debido a la conservación del momento lineal y la energía total. La producción de otra partícula también está prohibida debido a que ambas partículas (electrón-positrón) juntas no transportan suficiente energía de masa para producir partículas más pesadas. Cuando un electrón y un positrón chocan, se aniquilan, lo que resulta en la conversión completa de su masa en reposo a energía pura (de acuerdo con la fórmula E = mc 2 ) en forma de dos rayos gamma (fotones) de 0.511 MeV opuestos.
e – + e + → γ + γ (2x 0.511 MeV)
Este proceso debe cumplir una serie de leyes de conservación, que incluyen:
- Conservación de carga eléctrica. La carga neta antes y después es cero.
- Conservación del momento lineal y la energía total. T
- Conservación del momento angular.
……………………………………………………………………………………………………………………………….
Este artículo se basa en la traducción automática del artículo original en inglés. Para más información vea el artículo en inglés. Puedes ayudarnos. Si desea corregir la traducción, envíela a: [email protected] o complete el formulario de traducción en línea. Agradecemos su ayuda, actualizaremos la traducción lo antes posible. Gracias.