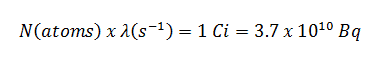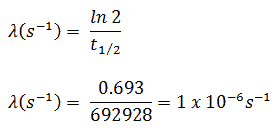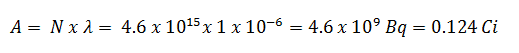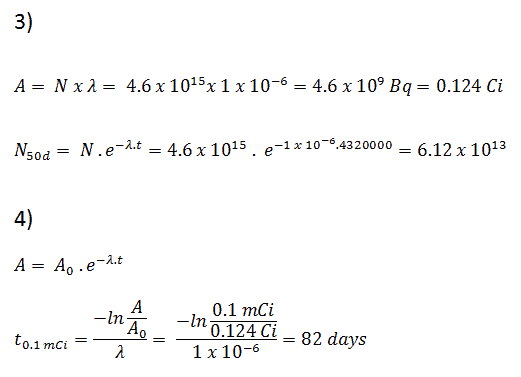La unidad SI para medir la cantidad de radiactividad es el becquerel (símbolo Bq ). El becquerel lleva el nombre en honor de Henri Becquerel, un físico francés que descubrió la radioactividad en 1896. Un becquerel (1Bq) equivale a 1 desintegración por segundo .
Una unidad más antigua de radiactividad es el curie. El curie se definió originalmente como equivalente al número de desintegraciones que sufrirá un gramo de radio-226 en un segundo. Actualmente, un curie se define usando becquerels como 1Ci = 3.7 x 10 10 desintegraciones por segundo. Por lo tanto
1Ci = 3.7 x 10 10 Bq = 37 GBq
Un becquerel es una cantidad muy pequeña de actividad. El cuerpo humano típico contiene aproximadamente 3.7 kBq (14 mg) de potasio-40 natural. Además, un cuerpo humano que contenga 16 kg de carbono también tendría aproximadamente 3,7 kBq de carbono-14 (24 nanogramos). Las actividades medidas en una planta de energía nuclear (excepto el combustible irradiado) a menudo tienen mayor actividad que el becquerel, y a menudo se usan los siguientes múltiplos:
1 kBq (kilobecquerel) = 1E3 Bq
1 MBq (megabecquerel) = 1E6 Bq
1 GBq (gigabecquerel) = 1E9 Bq
1 TBq (terabecquerel) = 1E12 Bq
Becquerel – Ejemplos
En la figura se muestra la relación entre la vida media y la cantidad de radionúclido requerida para dar una actividad de 37 GBq (1 Ci). Esta cantidad de material se puede calcular usando λ, que es la constante de descomposición de ciertos nucleidos:
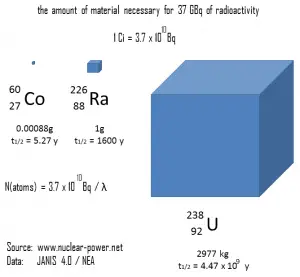 La siguiente figura ilustra la cantidad de material necesario para 37 GBq de radiactividad. Es obvio que cuanto más larga es la vida media, mayor es la cantidad de radionúclido necesaria para producir la misma actividad. Por supuesto, la sustancia de vida más larga permanecerá radiactiva durante mucho más tiempo. Como se puede ver, la cantidad de material necesaria para 37 GBq de radiactividad puede variar desde una cantidad demasiado pequeña para ser vista (0.00088 gramos de cobalto-60), hasta 1 gramo de radio-226, hasta casi tres toneladas de uranio-238 .
La siguiente figura ilustra la cantidad de material necesario para 37 GBq de radiactividad. Es obvio que cuanto más larga es la vida media, mayor es la cantidad de radionúclido necesaria para producir la misma actividad. Por supuesto, la sustancia de vida más larga permanecerá radiactiva durante mucho más tiempo. Como se puede ver, la cantidad de material necesaria para 37 GBq de radiactividad puede variar desde una cantidad demasiado pequeña para ser vista (0.00088 gramos de cobalto-60), hasta 1 gramo de radio-226, hasta casi tres toneladas de uranio-238 .
Ejemplo: cálculo de radiactividad
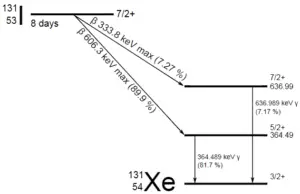 Una muestra de material contiene 1 microgramo de yodo-131. Tenga en cuenta que el yodo-131 desempeña un papel importante como isótopo radiactivo presente en los productos de fisión nuclear , y es un importante contribuyente a los riesgos para la salud cuando se libera a la atmósfera durante un accidente. El yodo 131 tiene una vida media de 8.02 días.
Una muestra de material contiene 1 microgramo de yodo-131. Tenga en cuenta que el yodo-131 desempeña un papel importante como isótopo radiactivo presente en los productos de fisión nuclear , y es un importante contribuyente a los riesgos para la salud cuando se libera a la atmósfera durante un accidente. El yodo 131 tiene una vida media de 8.02 días.
Calcular:
- El número de átomos de yodo-131 inicialmente presentes.
- La actividad del yodo-131 en curies.
- El número de átomos de yodo-131 que permanecerán en 50 días.
- El tiempo que le llevará a la actividad alcanzar 0.1 mCi.
Solución:
- El número de átomos de yodo-131 se puede determinar usando la masa isotópica como se muestra a continuación.
N I-131 = m I-131 . N A / M I-131
N I-131 = (1 μg) x (6.02 × 10 23 núcleos / mol) / (130.91 g / mol)
N I-131 = 4.6 x 10 15 núcleos
- La actividad del yodo-131 en los curies se puede determinar utilizando su constante de descomposición :
El yodo-131 tiene una vida media de 8.02 días (692928 segundos) y, por lo tanto, su constante de descomposición es:
Usando este valor para la constante de desintegración podemos determinar la actividad de la muestra:
3) y 4) El número de átomos de yodo-131 que permanecerán en 50 días (N 50d ) y el tiempo que le tomará a la actividad alcanzar 0.1 mCi se puede calcular usando la ley de descomposición:
Como se puede ver, después de 50 días, el número de átomos de yodo-131 y, por lo tanto, la actividad será aproximadamente 75 veces menor. Después de 82 días, la actividad será aproximadamente 1200 veces menor. Por lo tanto, el tiempo de diez vidas medias (factor 2 10 = 1024) se usa ampliamente para definir la actividad residual.
……………………………………………………………………………………………………………………………….
Este artículo se basa en la traducción automática del artículo original en inglés. Para más información vea el artículo en inglés. Puedes ayudarnos. Si desea corregir la traducción, envíela a: [email protected] o complete el formulario de traducción en línea. Agradecemos su ayuda, actualizaremos la traducción lo antes posible. Gracias.