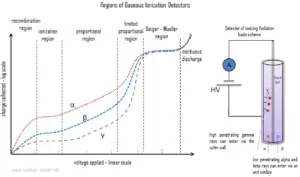
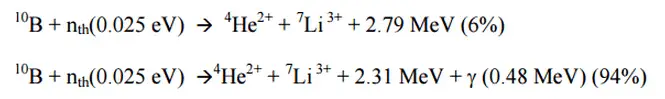A proportional counter, also known as the proportional detector, is an electrical device that detects various types of ionizing radiation. The voltage of detector is adjusted so that the conditions correspond to the proportional region. In this region, the voltage is high enough to provide the primary electrons with sufficient acceleration and energy so that they can ionize additional atoms of the medium. These secondary ions (gas amplification) formed are also accelerated causing an effect known as Townsend avalanches, which creates a single large electrical pulse. Gaseous proportional counters usually operate in high electric fields of the order of 10 kV/cm and achieve typical amplification factors of about 105. Since the amplification factor is strongly dependent on the applied voltage, the charge collected (output signal) is also dependent on the applied voltage and proportional counters require constant voltage.
This is a subtle, but important difference between ionization chambers and proportional counters. An ionization chamber will produce a current that is proportional to the number of electrons collected each second. This current is averaged and is used to drive a display reading in Bq, or μSv/h. Proportional counters do not work in this way. Instead, they amplify each of the individual bursts of ionisation so that each ionising event is detected separately. They therefore measure the number of ionising events (which is why they are called counters).
The process of charge amplification greatly improves the signal-to-noise ratio of the detector and reduces the subsequent electronic amplification required. When instruments are operated in the proportional region, the voltage must be kept constant. If a voltage remains constant the gas amplification factor also does not change. Proportional counter detection instruments are very sensitive to low levels of radiation. By proper functional arrangements, modifications, and biasing, the proportional counter can be used to detect alpha, beta, gamma, or neutron radiation in mixed radiation fields. Moreover, proportional counters are capable of particle identification and energy measurement (spectroscopy). The pulse height reflects the energy deposited by the incident radiation in the detector gas. As such, it is possible to distinguish the larger pulses produced by alpha particles from the smaller pulses produced by beta particles or gamma rays.
While ionization chambers can be operated in current or pulse mode, proportional counters or Geiger counters are almost always used in pulse mode. Detectors of ionizing radiation can be used both for activity measurements as well as for dose measurement. With knowledge about the energy needed to form an pair of ions – the dose can be obtained.
Application of Proportional Counters
Detection of Alpha, Beta and Gamma Radiation using Proportional Counter
Proportional counters in the form of large area planar detectors are used extensively to check for radioactive contamination on personnel, flat surfaces, tools, and items of clothing. Proportional counters are normally used to detect alpha and beta particles, and can enable discrimination between them by providing a pulse output proportional to the energy deposited in the chamber by each particle. They have a high efficiency for beta, but lower for alpha. For alpha and beta particles to be detected by proportional counters, they must be provided with a thin window. This “end-window” must be thin enough for the alpha and beta particles to penetrate. However, a window of almost any thickness will prevent an alpha particle from entering the chamber. The window is usually made of mica with a density of about 1.5 – 2.0 mg/cm2 to allow low-energy beta particles (e.g. from carbon-14) to enter the detector. The efficiency reduction for alpha is due to the attenuation effect of the end window, though distance from the surface being checked also has a significant effect, and ideally a source of alpha radiation should be less than 10mm from the detector due to attenuation in air.
Gamma rays have very little trouble in penetrating the metal walls of the chamber. Therefore, proportional counters may be used to detect gamma radiation and X-rays (thin-walled tubes) collectively known as photons, and for this the windowless tube is used.
The main drawback to using proportional counters in portable instruments is that they require a very stable power supply and amplifier to ensure constant operating conditions (in the middle of the proportional region). This is difficult to provide in a portable instrument, and that is why proportional counters tend to be used more in fixed or lab instruments.
Proportional Counter – Spectroscopy
In general, spectroscopes are devices designed to measure the spectral power distribution of a source. The incident radiation generates a signal that allows to determine the energy of the incident particle.
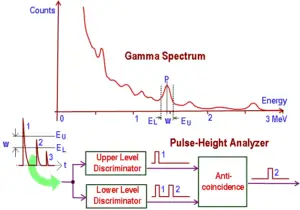
In proportional counters, the number of electrons produced is proportional to the energy and type of the incident particle. Therefore, proportional counters are capable of particle identification and energy measurement (spectroscopy). Different energies of radiation and different types of radiation can be distinguished by analyzing the pulse height, since they significantly differ in the primary ionization (low-LET vs high-LET). Proportional counters may be used for example to analyse a spectrum of alpha radiations or a spectrum of beta particles. The energy resolution of a proportional counter, however, is limited because both the initial ionization event and the subsequent ‘multiplication’ event are subject to statistical fluctuations characterized by a standard deviation equal to the square root of the average number formed.
A large volume spherical proportional counter can be used for neutron measurements. The pure N2 gas is studied for thermal and fast neutron detection, providing a new way for neutron spectroscopy. The neutrons are detected via the 14N(n,p)14C and 14N(n,α)11B reactions.
It must be noted, for gamma spectrometry, the most common detectors include sodium iodide (NaI) scintillation counters and high-purity germanium detectors.
Multi-wire Proportional Chamber – MWPC
A multi-wire proportional chamber is a type of proportional counter used especially in high energy particle physics to detect charged particles and photons and can give positional information on their trajectory. This device was developed by Georges Charpak and his collaborators. This invention resulted in him winning the Nobel Prize for Physics in 1992. The multi-wire chamber uses an array of wires at high voltage (anode), which run through a chamber with conductive walls held at ground potential (cathode). The principle is to have a plane of anode wires positioned precisely, with typical wire-spacings of about 2 mm. By computing pulses from all the wires, the particle trajectory can be found.
Detection of Neutrons using Proportional Counter
Since the neutrons are electrically neutral particles, they are mainly subject to strong nuclear forces but not to electric forces. Therefore neutrons are not directly ionizing and they have usually to be converted into charged particles before they can be detected. Generally every type of neutron detector must be equipped with converter (to convert neutron radiation to common detectable radiation) and one of the conventional radiation detectors (scintillation detector, gaseous detector, semiconductor detector, etc.).
Proportional counters are often used as the charged particle detection device. In nuclear power plants, gas-filled (BF3) proportional counters are normally used as source range detectors. These detectors use the gas boron trifluoride (BF3) instead of air in the chamber. The incoming neutrons produce alpha particles when they react with the boron atoms in the detector gas. Most of (n,alpha) reactions of thermal neutrons are 10B(n,alpha)7Li reactions accompanied by 0.48 MeV gamma emission.
Moreover, isotope boron-10 has high (n,alpha) reaction cross-section along the entire neutron energy spectrum. The alpha particle causes ionization within the chamber, and ejected electrons cause further secondary ionizations.
Proportional counter output is in the form of one pulse for every ionizing event; therefore, there is a series of random pulses varying in magnitude representing neutron and gamma ionizing events. The pulse height may only be a few millivolts, which is too low to be directly used without amplification. The discriminator excludes passage of pulses that are less than a predetermined level. The function of the discriminator is to exclude noise and gamma pulses that are lower in magnitude than neutron pulses.
We hope, this article, Application of Proportional Counters, helps you. If so, give us a like in the sidebar. Main purpose of this website is to help the public to learn some interesting and important information about radiation and dosimeters.