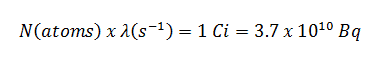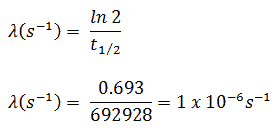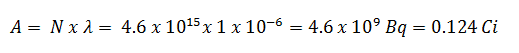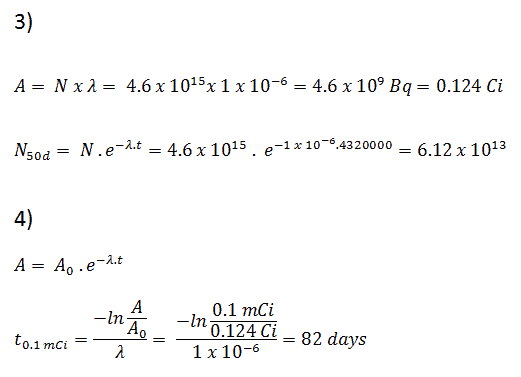Na física nuclear e na química nuclear, as várias espécies de átomos cujos núcleos contêm números particulares de prótons e nêutrons são chamadas nuclídeos . Os nuclídeos também são caracterizados por seus estados de energia nuclear (por exemplo, nuclídeo metaestável 242m Am). Cada nuclídeo é indicado pelo símbolo químico do elemento (isso especifica Z) com o número de massa atômica como sobrescrito. Isótopos são nuclídeos que possuem o mesmo número atômico e, portanto, são o mesmo elemento, mas diferem no número de nêutrons.
Existem nuclídeos instáveis e radioativos. Esses nuclídeos são conhecidos como radionuclídeos (nuclídeos radioativos) ou radioisótopos (isótopos radioativos). Esses isótopos instáveis decaem através de várias vias de decaimento radioativo, mais comumente decaimento alfa, decaimento beta, decaimento gama ou captura de elétrons. Muitos outros tipos raros de deterioração, como fissão espontânea ou emissão de nêutrons, são conhecidos.
Como foi escrito, o decaimento radioativo dos radionuclídeos é um processo aleatório no nível de átomos únicos, pois, segundo a teoria quântica, é impossível prever quando um átomo em particular decairá. Em outras palavras, um núcleo de um radionuclídeo não tem “memória”. Um núcleo não “envelhece” com o passar do tempo. Assim, a probabilidade de quebra não aumenta com o tempo, mas permanece constante, não importa quanto tempo o núcleo exista.
Portanto, a taxa de decaimento nuclear também pode ser medida em termos de meia-vida . Cada radionuclídeo tem sua meia-vida particular que nunca muda, independentemente da quantidade ou forma do material (isto é, sólido, líquido, gás, elemento ou composto) ou seu histórico passado. Se um radioisótopo tiver meia-vida de 14 dias, metade de seus átomos terá decaimento em 14 dias. Em mais 14 dias, metade da metade restante decairá e assim por diante.
As meias-vidas variam de milionésimos de segundo para produtos de fissão altamente radioativos a bilhões de anos para materiais de longa duração (como o urânio que ocorre naturalmente). Após cinco meia-vidas, apenas 1/32, ou 3,1%, do número original de átomos permanece. Após sete meias-vidas, apenas 1/128, ou 0,78%, dos átomos permanecem. O número de átomos existentes após 5 a 7 meias-vidas pode geralmente ser considerado insignificante.
A fração da atividade original restante após meias-vidas sucessivas é:
Atividade após 1 meia-vida = ½ da original
Atividade após 2 meias-vidas = ½ x ½ = ¼ do original
Atividade após 3 semi-vidas = ½ x ½ x ½ = (½) 3 = 1/8 do original
Atividade após 4 meias-vidas = (½) 4 = 1/16 do original
Atividade após 5 semi-vidas = (½) 5 = 1/32 do original
Atividade após 6 semi-vidas = (½) 6 = 1/64 do original
Atividade após 7 meias-vidas = (½) 7 = 1/128 do original
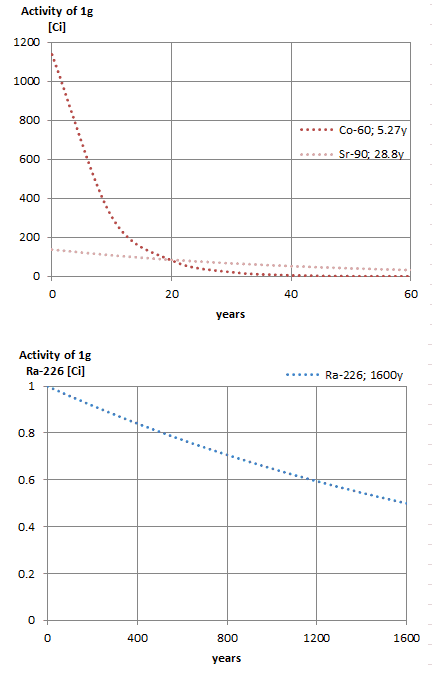 Observe que as meias-vidas curtas seguem grandes constantes de decaimento. O material radioativo com meia-vida curta é muito mais radioativo (no momento da produção), mas obviamente perderá sua radioatividade rapidamente. Não importa quanto tempo a meia-vida seja curta ou curta, depois que sete meias-vidas tiverem passado, resta menos de 1% da atividade inicial.
Observe que as meias-vidas curtas seguem grandes constantes de decaimento. O material radioativo com meia-vida curta é muito mais radioativo (no momento da produção), mas obviamente perderá sua radioatividade rapidamente. Não importa quanto tempo a meia-vida seja curta ou curta, depois que sete meias-vidas tiverem passado, resta menos de 1% da atividade inicial.
A lei de decaimento radioativo afirma que a probabilidade por unidade de tempo que um núcleo decairá é uma constante, independente do tempo. Essa constante é chamada constante de decaimento e é denotada por λ, “lambda”. Essa probabilidade constante pode variar muito entre os diferentes tipos de núcleos, levando a muitas taxas diferentes de decaimento observadas. O decaimento radioativo de certo número de átomos (massa) é exponencial no tempo.
Lei de decaimento radioativo: N = Ne -λt
A lei de decaimento radioativo também pode ser derivada para cálculos de atividade ou massa de cálculos de material radioativo:
(Número de núcleos) N = Ne -λt (Atividade) A = Ae -λt (Massa) m = me -λt
, onde N (número de partículas) é o número total de partículas na amostra, A (atividade total) é o número de decaimentos por unidade de tempo de uma amostra radioativa, m é a massa do material radioativo restante.
Meia-vida e radioatividade de radionuclídeos
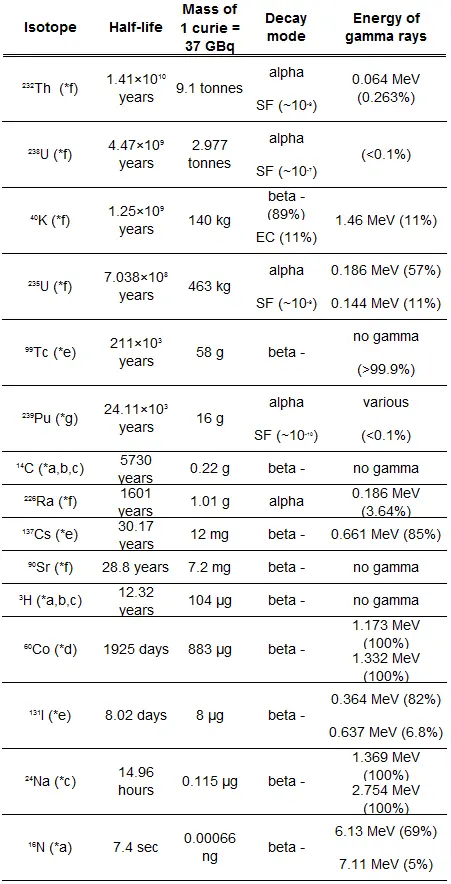
A relação entre a meia-vida e a quantidade de radionuclídeo necessária para gerar uma atividade de um curie é mostrada na figura. Essa quantidade de material pode ser calculada usando λ , que é a constante de decaimento de determinado nuclídeo:
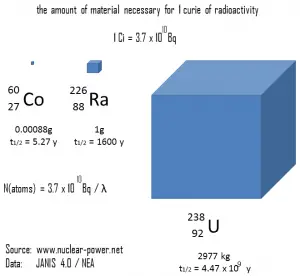 A figura a seguir ilustra a quantidade de material necessário para 1 curie de radioatividade. É óbvio que quanto maior a meia-vida, maior a quantidade de radionuclídeo necessária para produzir a mesma atividade. Evidentemente, a substância de vida mais longa permanecerá radioativa por muito mais tempo. Como pode ser visto, a quantidade de material necessário para 1 curie de radioatividade pode variar de uma quantidade muito pequena para ser vista (0,00088 grama de cobalto-60), através de 1 grama de rádio-226, a quase três toneladas de urânio-238 .
A figura a seguir ilustra a quantidade de material necessário para 1 curie de radioatividade. É óbvio que quanto maior a meia-vida, maior a quantidade de radionuclídeo necessária para produzir a mesma atividade. Evidentemente, a substância de vida mais longa permanecerá radioativa por muito mais tempo. Como pode ser visto, a quantidade de material necessário para 1 curie de radioatividade pode variar de uma quantidade muito pequena para ser vista (0,00088 grama de cobalto-60), através de 1 grama de rádio-226, a quase três toneladas de urânio-238 .
Exemplo – Radioatividade do Radionuclídeo
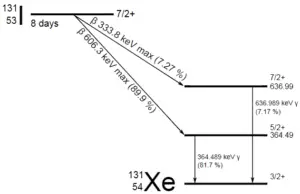 Uma amostra de material contém 1 micrograma de iodo-131. Observe que o iodo-131 desempenha um papel importante como isótopo radioativo presente nos produtos de fissão nuclear e é um dos principais contribuintes para os riscos à saúde quando liberado na atmosfera durante um acidente. O iodo-131 tem uma meia-vida de 8,02 dias.
Uma amostra de material contém 1 micrograma de iodo-131. Observe que o iodo-131 desempenha um papel importante como isótopo radioativo presente nos produtos de fissão nuclear e é um dos principais contribuintes para os riscos à saúde quando liberado na atmosfera durante um acidente. O iodo-131 tem uma meia-vida de 8,02 dias.
Calcular:
- O número de átomos de iodo-131 inicialmente presentes.
- A atividade do iodo-131 nos curies.
- O número de átomos de iodo-131 que permanecerá em 50 dias.
- O tempo necessário para a atividade atingir 0,1 mCi.
Solução:
- O número de átomos de iodo-131 pode ser determinado usando a massa isotópica como abaixo.
N -131 = m I-131 . N A / H I-131
NI -131 = (1 μg) x (6,02 × 10 23 núcleos / mol) / (130,91 g / mol)
NI -131 = 4,6 x 10 15 núcleos
- A atividade do iodo-131 em curies pode ser determinada usando sua constante de decaimento :
O iodo-131 tem meia-vida de 8,02 dias (692928 seg) e, portanto, sua constante de decaimento é:
Usando esse valor para a constante de decaimento, podemos determinar a atividade da amostra:
3) e 4) O número de átomos de iodo-131 que permanecerá em 50 dias (N 50d ) e o tempo necessário para a atividade atingir 0,1 mCi podem ser calculados usando a lei de decaimento:
Como pode ser visto, após 50 dias o número de átomos de iodo-131 e, portanto, a atividade será cerca de 75 vezes menor. Após 82 dias, a atividade será aproximadamente 1200 vezes menor. Portanto, o tempo de dez meias-vidas (fator 2 10 = 1024) é amplamente utilizado para definir a atividade residual.
……………………………………………………………………………………………………………………………….
Este artigo é baseado na tradução automática do artigo original em inglês. Para mais informações, consulte o artigo em inglês. Você pode nos ajudar. Se você deseja corrigir a tradução, envie-a para: [email protected] ou preencha o formulário de tradução on-line. Agradecemos sua ajuda, atualizaremos a tradução o mais rápido possível. Obrigado.