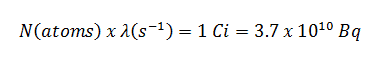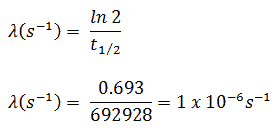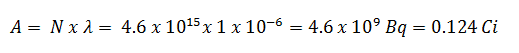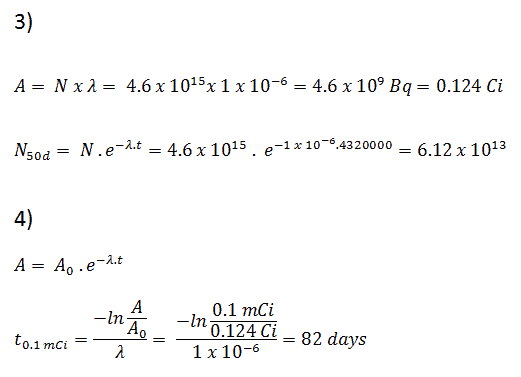O que é constante de decaimento – Definição

A lei de decaimento radioativo afirma que a probabilidade por unidade de tempo que um núcleo decairá é uma constante, independente do tempo. Essa constante é chamada constante de decaimento e é denotada por λ, “lambda”. Essa probabilidade constante pode variar muito entre os diferentes tipos de núcleos, levando a muitas taxas diferentes de decaimento observadas. O decaimento radioativo de certo número de átomos (massa) é exponencial no tempo.

Lei de decaimento radioativo: N = Ne- ^λt

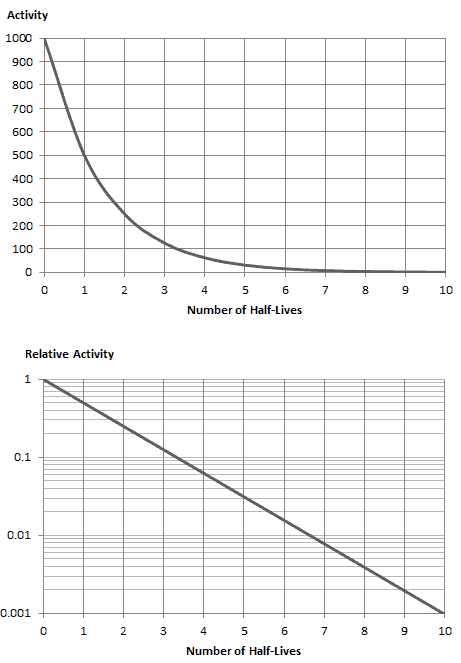
A taxa de decaimento nuclear também é medida em termos de meia-vida . A meia-vida é a quantidade de tempo que um determinado isótopo leva para perder metade de sua radioatividade. Se um radioisótopo tiver meia-vida de 14 dias, metade de seus átomos terá decaimento em 14 dias. Em mais 14 dias, metade da metade restante decairá e assim por diante. As meias-vidas variam de milionésimos de segundo para produtos de fissão altamente radioativos a bilhões de anos para materiais de longa duração (como o urânio que ocorre naturalmente). Notar quemeia-vida curta acompanha grandes constantes de decaimento. O material radioativo com meia-vida curta é muito mais radioativo (no momento da produção), mas obviamente perderá sua radioatividade rapidamente. Não importa quanto tempo a meia-vida seja curta ou curta, depois que sete meias-vidas tiverem passado, resta menos de 1% da atividade inicial.

A lei de decaimento radioativo também pode ser derivada para cálculos de atividade ou massa de cálculos de material radioativo:

(Número de núcleos) N = Ne ^-λt     (Atividade) A = Ae ^-λt      (Massa) m = me ^-λt

, onde N (número de partículas) é o número total de partículas na amostra, A (atividade total) é o número de decaimentos por unidade de tempo de uma amostra radioativa, m é a massa do material radioativo restante.

Decaimento constante e meia-vida

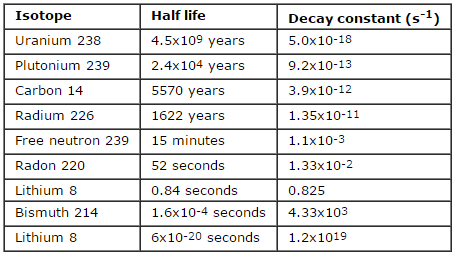
Nos cálculos de radioatividade, um dos dois parâmetros ( constante de decaimento ou meia-vida ), que caracterizam a taxa de decaimento, deve ser conhecido. Existe uma relação entre a meia-vida (t _1/2 ) e a constante de decaimento λ. O relacionamento pode ser derivado da lei de decaimento, definindo N = ½ N _o . Isto dá:

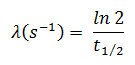onde ln 2 (o logaritmo natural de 2) é igual a 0,693. Se a constante de decaimento (λ) for dada, é fácil calcular a meia-vida e vice-versa.

Constante de decaimento e radioatividade

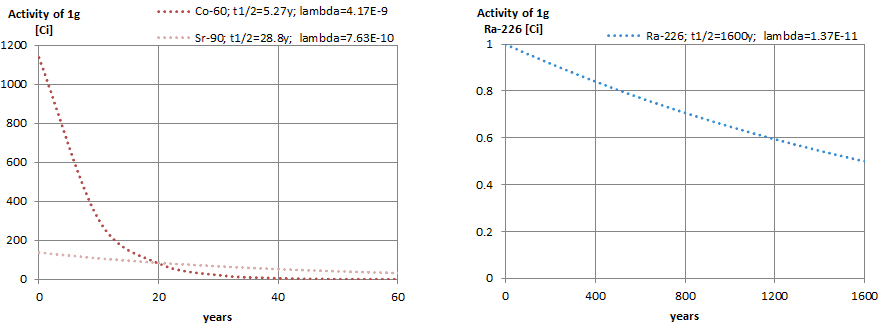
A relação entre a meia-vida e a quantidade de radionuclídeo necessária para gerar uma atividade de um curie é mostrada na figura. Essa quantidade de material pode ser calculada usando λ , que é a constante de decaimento de determinado nuclídeo:

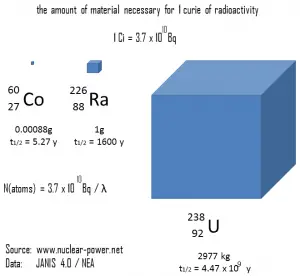A figura a seguir ilustra a quantidade de material necessário para 1 curie de radioatividade. É óbvio que quanto maior a meia-vida, maior a quantidade de radionuclídeo necessária para produzir a mesma atividade. Evidentemente, a substância de vida mais longa permanecerá radioativa por muito mais tempo. Como pode ser visto, a quantidade de material necessário para 1 curie de radioatividade pode variar de uma quantidade muito pequena para ser vista (0,00088 grama de cobalto-60), através de 1 grama de rádio-226, a quase três toneladas de urânio-238 .

Exemplo – Cálculo de Radioatividade

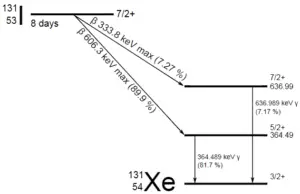Uma amostra de material contém 1 micrograma de iodo-131. Observe que o iodo-131 desempenha um papel importante como isótopo radioativo presente nos produtos de fissão nuclear e é um dos principais contribuintes para os riscos à saúde quando liberado na atmosfera durante um acidente. O iodo-131 tem uma meia-vida de 8,02 dias.

Calcular:

1. O número de átomos de iodo-131 inicialmente presentes.
2. A atividade do iodo-131 nos curies.
3. O número de átomos de iodo-131 que permanecerá em 50 dias.
4. O tempo necessário para a atividade atingir 0,1 mCi.

Solução:

1. O número de átomos de iodo-131 pode ser determinado usando a massa isotópica como abaixo.

N _-131 = m _I-131 . N _A / H _I-131

NI _-131 = (1 μg) x (6,02 × 10 ²³ núcleos / mol) / (130,91 g / mol)

NI _-131 = 4,6 x 10 ¹⁵ núcleos

2. A atividade do iodo-131 em curies pode ser determinada usando sua constante de decaimento :

O iodo-131 tem meia-vida de 8,02 dias (692928 seg) e, portanto, sua constante de decaimento é:

Usando esse valor para a constante de decaimento, podemos determinar a atividade da amostra:

3) e 4) O número de átomos de iodo-131 que permanecerá em 50 dias (N _50d ) e o tempo necessário para a atividade atingir 0,1 mCi podem ser calculados usando a lei de decaimento:

Como pode ser visto, após 50 dias o número de átomos de iodo-131 e, portanto, a atividade será cerca de 75 vezes menor. Após 82 dias, a atividade será aproximadamente 1200 vezes menor. Portanto, o tempo de dez meias-vidas (fator 2 ¹⁰ = 1024) é amplamente utilizado para definir a atividade residual.