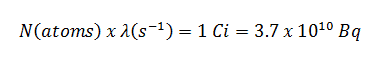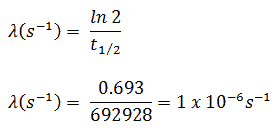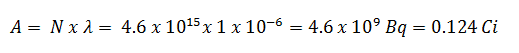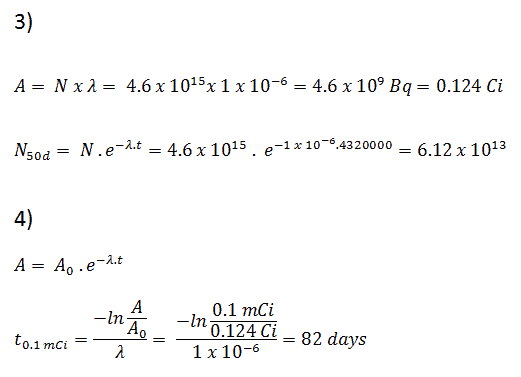Was ist die Berechnung der Radioaktivität aus der Zerfallskonstante – Definition

Zerfallskonstante und Radioaktivität

Die Beziehung zwischen der Halbwertszeit und der Menge eines Radionuklids, die erforderlich ist, um eine Aktivität von einem Curie zu ergeben, ist in der Figur gezeigt. Diese Materialmenge kann mit λ berechnet werden , was die Zerfallskonstante eines bestimmten Nuklids ist:

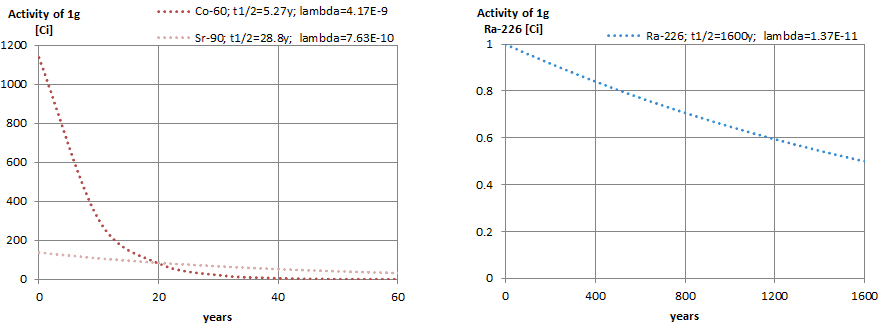
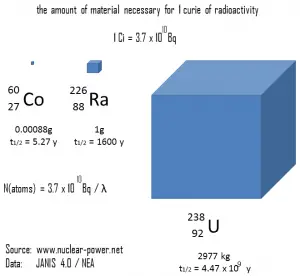Die folgende Abbildung zeigt die Menge an Material, die für 1 Curie Radioaktivität erforderlich ist . Es ist offensichtlich, dass je länger die Halbwertszeit ist, desto mehr Radionuklid wird benötigt, um die gleiche Aktivität zu erzeugen. Natürlich bleibt die länger lebende Substanz viel länger radioaktiv. Wie zu sehen ist, kann die Menge an Material, die für 1 Curie Radioaktivität erforderlich ist, von einer zu geringen Menge (0,00088 Gramm Cobalt-60) über 1 Gramm Radium-226 bis zu fast drei Tonnen Uran-238 variieren .

Beispiel – Berechnung der Radioaktivität

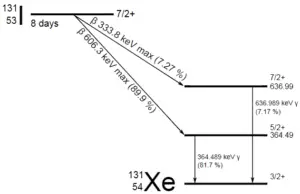Eine Materialprobe enthält 1 Mikrogramm Jod-131. Es ist zu beachten, dass Iod-131 eine wichtige Rolle als radioaktives Isotop in Kernspaltungsprodukten spielt und einen wesentlichen Beitrag zu den Gesundheitsgefahren leistet, wenn es während eines Unfalls in die Atmosphäre freigesetzt wird. Jod-131 hat eine Halbwertszeit von 8,02 Tagen.

Berechnung:

1. Die Anzahl der anfangs vorhandenen Iod-131-Atome.
2. Die Aktivität des Jod-131 in Curies.
3. Die Anzahl der Iod-131-Atome, die in 50 Tagen verbleiben.
4. Die Zeit, die die Aktivität benötigt, um 0,1 mCi zu erreichen.

Lösung:

1. Die Anzahl der Atome von Iod-131 kann unter Verwendung der Isotopenmasse wie folgt bestimmt werden.

N _I-131 = m _I-131 . N _A / M _I-131

N _I-131 = (1 & mgr; g ) x (6,02 × 10 ²³ Kerne / mol) / (130,91 g / mol)

N _I-131 = 4,6 × 10 ¹⁵ Kerne

2. Die Aktivität des Iod-131 in Curies kann anhand seiner Zerfallskonstante bestimmt werden :

Das Jod-131 hat eine Halbwertszeit von 8,02 Tagen (692928 Sekunden) und daher ist seine Zerfallskonstante:

Mit diesem Wert für die Abklingkonstante können wir die Aktivität der Probe bestimmen:

3) und 4) Die Anzahl der Iod-131-Atome, die in 50 Tagen verbleiben (N _50d ), und die Zeit, die die Aktivität benötigt, um 0,1 mCi zu erreichen, können unter Verwendung des Zerfallsgesetzes berechnet werden:

Wie zu sehen ist, wird nach 50 Tagen die Anzahl der Iod-131-Atome und damit die Aktivität etwa 75-mal geringer sein. Nach 82 Tagen ist die Aktivität ungefähr 1200-mal geringer. Daher wird die Zeit von zehn Halbwertszeiten (Faktor 2 ¹⁰ = 1024) häufig verwendet, um die Restaktivität zu definieren.