- σf – Photoelectric effect
- σC – Compton scattering
- σp – Pair production
Depending on the gamma ray energy and the absorber material, one of the three partial cross-sections may become much larger than the other two. At small values of gamma ray energy the photoelectric effect dominates. Compton scattering dominates at intermediate energies. The compton scattering also increases with decreasing atomic number of matter, therefore the interval of domination is wider for light nuclei. Finally, electron-positron pair production dominates at high energies.Based on the definition of interaction cross-section, the dependence of gamma rays intensity on thickness of absorber material can be derive. If monoenergetic gamma rays are collimated into a narrow beam and if the detector behind the material only detects the gamma rays that passed through that material without any kind of interaction with this material, then the dependence should be simple exponential attenuation of gamma rays. Each of these interactions removes the photon from the beam either by absorbtion or by scattering away from the detector direction. Therefore the interactions can be characterized by a fixed probability of occurance per unit path length in the absorber. The sum of these probabilities is called the linear attenuation coefficient:
μ = τ(photoelectric) + σ(Compton) + κ(pair)
Linear Attenuation Coefficient
The attenuation of gamma radiation can be then described by the following equation.
I=I0.e-μx
, where I is intensity after attenuation, Io is incident intensity, μ is the linear attenuation coefficient (cm-1), and physical thickness of absorber (cm).
The materials listed in the table beside are air, water and a different elements from carbon (Z=6) through to lead (Z=82) and their linear attenuation coefficients are given for three gamma ray energies. There are two main features of the linear attenuation coefficient:
- The linear attenuation coefficient increases as the atomic number of the absorber increases.
- The linear attenuation coefficient for all materials decreases with the energy of the gamma rays.
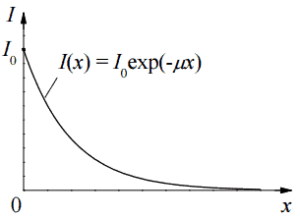 Dependence of gamma radiation intensity on absorber thickness.
Dependence of gamma radiation intensity on absorber thickness.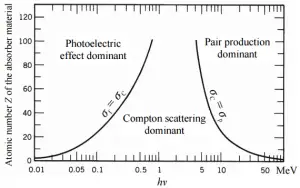 The relative importance of various processes of gamma radiation interaction with matter.Linear Attenuation Coefficients
The relative importance of various processes of gamma radiation interaction with matter.Linear Attenuation Coefficients
Table of Linear Attenuation Coefficients (in cm-1) for a different materials at gamma ray energies of 100, 200 and 500 keV.
| Absorber | 100 keV | 200 keV | 500 keV |
| Air | 0.000195/cm | 0.000159/cm | 0.000112/cm |
| Water | 0.167/cm | 0.136/cm | 0.097/cm |
| Carbon | 0.335/cm | 0.274/cm | 0.196/cm |
| Aluminium | 0.435/cm | 0.324/cm | 0.227/cm |
| Iron | 2.72/cm | 1.09/cm | 0.655/cm |
| Copper | 3.8/cm | 1.309/cm | 0.73/cm |
| Lead | 59.7/cm | 10.15/cm | 1.64/cm |
We hope, this article, Linear Attenuation Coefficient, helps you. If so, give us a like in the sidebar. Main purpose of this website is to help the public to learn some interesting and important information about radiation and dosimeters.