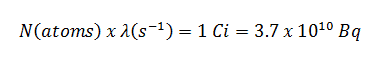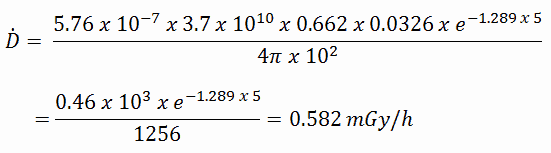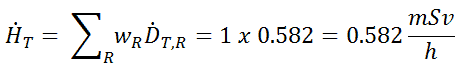 In radiation protection, the sievert is a derived unit of equivalent dose and effective dose. The sievert represents the equivalent biological effect of the deposit of a joule of gamma rays energy in a kilogram of human tissue. Unit of sievert is of importance in radiation protection and was named after the Swedish scientist Rolf Sievert, who did a lot of the early work on dosimetry in radiation therapy.
In radiation protection, the sievert is a derived unit of equivalent dose and effective dose. The sievert represents the equivalent biological effect of the deposit of a joule of gamma rays energy in a kilogram of human tissue. Unit of sievert is of importance in radiation protection and was named after the Swedish scientist Rolf Sievert, who did a lot of the early work on dosimetry in radiation therapy.
Calculation of Shielded Dose Rate in Sieverts
Assume the point isotropic source which contains 1.0 Ci of 137Cs, which has a half-life of 30.2 years. Note that the relationship between half-life and the amount of a radionuclide required to give an activity of one curie is shown below. This amount of material can be calculated using λ, which is the decay constant of certain nuclide:
About 94.6 percent decays by beta emission to a metastable nuclear isomer of barium: barium-137m. The main photon peak of Ba-137m is 662 keV. For this calculation, assume that all decays go through this channel.
Calculate the primary photon dose rate, in gray per hour (Gy.h-1), at the outer surface of a 5 cm thick lead shield. Then calculate the equivalent dose rate. Assume that this external radiation field penetrate uniformly through the whole body. Primary photon dose rate neglects all secondary particles. Assume that the effective distance of the source from the dose point is 10 cm. We shall also assume that the dose point is soft tissue and it can reasonably be simulated by water and we use the mass energy absorption coefficient for water.
See also: Gamma Ray Attenuation
See also: Shielding of Gamma Rays
Solution:
The primary photon dose rate is attenuated exponentially, and the dose rate from primary photons, taking account of the shield, is given by:
As can be seen, we do not account for the buildup of secondary radiation. If secondary particles are produced or if the primary radiation changes its energy or direction, then the effective attenuation will be much less. This assumption generally underestimates the true dose rate, especially for thick shields and when the dose point is close to the shield surface, but this assumption simplifies all calculations. For this case the true dose rate (with the buildup of secondary radiation) will be more than two times higher.
To calculate the absorbed dose rate, we have to use in the formula:
- k = 5.76 x 10-7
- S = 3.7 x 1010 s-1
- E = 0.662 MeV
- μt/ρ = 0.0326 cm2/g (values are available at NIST)
- μ = 1.289 cm-1 (values are available at NIST)
- D = 5 cm
- r = 10 cm
Result:
The resulting absorbed dose rate in grays per hour is then:
Since the radiation weighting factor for gamma rays is equal to one and we have assumed the uniform radiation field, we can directly calculate the equivalent dose rate from the absorbed dose rate as:
If we want to account for the buildup of secondary radiation, then we have to include the buildup factor. The extended formula for the dose rate is then:
——–
We hope, this article, Calculation of Shielded Dose Rate in Sieverts, helps you. If so, give us a like in the sidebar. Main purpose of this website is to help the public to learn some interesting and important information about radiation and dosimeters.