Les rayons X , également connus sous le nom de rayonnement X , se réfèrent au rayonnement électromagnétique (pas de masse au repos, pas de charge) des hautes énergies. Les rayons X sont des photons de haute énergie avec des longueurs d’onde courtes et donc des fréquences très élevées. La fréquence de rayonnement est un paramètre clé de tous les photons, car elle détermine l’énergie d’un photon. Les photons sont classés en fonction des énergies des ondes radioélectriques de faible énergie et du rayonnement infrarouge, à travers la lumière visible, aux rayons X à haute énergie et aux rayons gamma .
La plupart des rayons X ont une longueur d’onde allant de 0,01 à 10 nanomètres (3 × 10 16 Hz à 3 × 10 19 Hz), correspondant à des énergies comprises entre 100 eV et 100 keV. Les longueurs d’onde des rayons X sont plus courtes que celles des rayons UV et généralement plus longues que celles des rayons gamma. La distinction entre les rayons X et les rayons gamma n’est pas si simple et a changé au cours des dernières décennies. Selon la définition actuellement valable, les rayons X sont émis par des électrons à l’extérieur du noyau, tandis que les rayons gamma sont émis par le noyau .
Atténuation des rayons X
Source: Wikimedia Commons
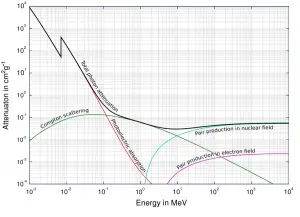
À mesure que les photons de haute énergie traversent le matériau, leur énergie diminue. C’est ce qu’on appelle l’ atténuation . La théorie de l’atténuation est également valable pour les rayons X et les rayons gamma . Il s’avère que les photons de plus haute énergie (rayons X durs) voyagent à travers les tissus plus facilement que les photons de basse énergie (c’est-à-dire que les photons de plus haute énergie sont moins susceptibles d’interagir avec la matière). Une grande partie de cet effet est liée à l’ effet photoélectrique . La probabilité d’absorption photoélectrique est approximativement proportionnelle à (Z / E) 3, où Z est le numéro atomique de l’atome de tissu et E est l’énergie photonique. À mesure que E augmente, la probabilité d’interaction diminue rapidement. Pour les énergies supérieures, la diffusion Compton devient dominante. La diffusion de Compton est à peu près constante pour différentes énergies bien qu’elle diminue lentement aux énergies plus élevées.
Atténuation exponentielle
Supposons que les rayons X monoénergétiques sont collimatés en un faisceau étroit et que le détecteur derrière le matériau détecte uniquement les rayons X qui ont traversé ce matériau sans aucune sorte d’interaction avec ce matériau, alors la dépendance devrait être une simple atténuation exponentielle des rayons X . Chacune de ces interactions élimine le photon du faisceau soit par absorption, soit par diffusion loin de la direction du détecteur. Par conséquent, les interactions peuvent être caractérisées par une probabilité fixe d’occurrence par unité de longueur de trajet dans l’absorbeur. La somme de ces probabilités est appelée coefficient d’atténuation linéaire :
μ = τ (photoélectrique) + σ (Compton)
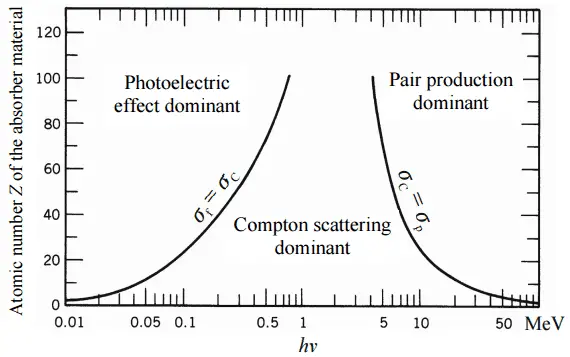
Coefficient d’atténuation linéaire – rayons X
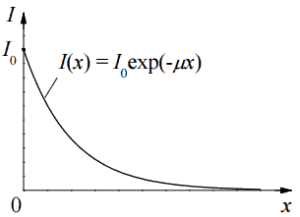
L’atténuation des rayons X peut alors être décrite par l’équation suivante.
I = I 0 .e -μx
, où I est l’intensité après atténuation, I o est l’intensité incidente, μ est le coefficient d’atténuation linéaire (cm -1 ) et l’épaisseur physique de l’absorbeur (cm).
Les matériaux répertoriés dans le tableau sont l’air, l’eau et différents éléments du carbone ( Z = 6) au plomb ( Z = 82) et leurs coefficients d’atténuation linéaires sont donnés pour deux énergies de rayons X. Il existe deux caractéristiques principales du coefficient d’atténuation linéaire:
- Le coefficient d’atténuation linéaire augmente à mesure que le numéro atomique de l’absorbeur augmente.
- Le coefficient d’atténuation linéaire pour tous les matériaux diminue avec l’énergie des rayons X.
Demi couche de valeur
La couche à demi-valeur exprime l’épaisseur du matériau absorbant nécessaire pour réduire l’intensité du rayonnement incident d’un facteur deux . Il existe deux caractéristiques principales de la couche de demi-valeur:
- La couche de demi-valeur diminue à mesure que le numéro atomique de l’absorbeur augmente. Par exemple, 35 m d’air sont nécessaires pour réduire l’intensité d’un faisceau de rayons X de 100 keV par un facteur de deux alors que seulement 0,12 mm de plomb peut faire la même chose.
- La couche de demi-valeur pour tous les matériaux augmente avec l’énergie des rayons X. Par exemple, de 0,26 cm pour le fer à 100 keV à environ 0,64 cm à 200 keV.
Coefficient d’atténuation de masse
Lors de la caractérisation d’un matériau absorbant, on peut parfois utiliser le coefficient d’atténuation massique. Le coefficient d’atténuation massique est défini comme le rapport du coefficient d’atténuation linéaire et de la densité d’absorbeur (μ / ρ) . L’ atténuation des rayons X peut alors être décrite par l’équation suivante:
I = I 0 .e – (μ / ρ) .ρl
, où ρ est la densité du matériau, (μ / ρ) est le coefficient d’atténuation de la masse et ρ.l est l’épaisseur de la masse. L’unité de mesure utilisée pour le coefficient d’atténuation de masse cm 2 g -1 . Pour les énergies intermédiaires, la diffusion Compton domine et différents absorbeurs ont des coefficients d’atténuation de masse approximativement égaux . Cela est dû au fait que la section efficace de la diffusion Compton est proportionnelle au Z (numéro atomique) et donc le coefficient est proportionnel à la densité du matériau ρ. Aux petites valeurs de l’énergie des rayons X, où le coefficient est proportionnel aux puissances supérieures du numéro atomique Z (pour l’effet photoélectrique σ f ~ Z 3 ), le coefficient d’atténuation μ n’est pas une constante.
Voir aussi calculatrice: Activité gamma au débit de dose (avec / sans écran)
Voir aussi XCOM – photon cross-section DB: XCOM: Photon Cross Sections Database
Exemple:
De quelle quantité d’eau absorbez-vous la chaleur si vous souhaitez réduire l’intensité d’un faisceau de rayons X monoénergétique de 100 keV ( faisceau étroit ) à 1% de son intensité incidente? La couche de demi-valeur pour les rayons X à 100 keV dans l’eau est de 4,15 cm et le coefficient d’atténuation linéaire pour les rayons X à 100 keV dans l’eau est de 0,167 cm -1 . Le problème est assez simple et peut être décrit par l’équation suivante:
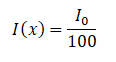 Si la demi-couche de valeur pour l’eau est de 4,15 cm, le coefficient d’atténuation linéaire est:
Si la demi-couche de valeur pour l’eau est de 4,15 cm, le coefficient d’atténuation linéaire est: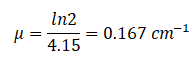 Maintenant, nous pouvons utiliser l’équation d’atténuation exponentielle:
Maintenant, nous pouvons utiliser l’équation d’atténuation exponentielle: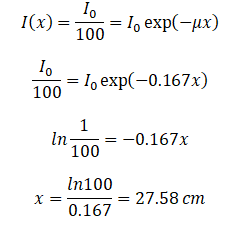
L’épaisseur d’eau requise est donc d’environ 27,58 cm . C’est une épaisseur relativement importante et elle est causée par de petits nombres atomiques d’hydrogène et d’oxygène. Si nous calculons le même problème pour le plomb (Pb) , nous obtenons l’épaisseur x = 0,077 cm .
Coefficients d’atténuation linéaire
Tableau des coefficients d’atténuation linéaire (en cm -1 ) pour différents matériaux à des énergies de photons de 100, 200 et 500 keV.
| Absorbeur | 100 keV | 200 keV | 500 keV |
| Air | 0,000195 / cm | 0,000159 / cm | 0,000112 / cm |
| Eau | 0,167 / cm | 0,136 / cm | 0,097 / cm |
| Carbone | 0,335 / cm | 0,274 / cm | 0,196 / cm |
| Aluminium | 0,435 / cm | 0,324 / cm | 0,227 / cm |
| Le fer | 2,72 / cm | 1,09 / cm | 0,655 / cm |
| Cuivre | 3,8 / cm | 1,309 / cm | 0,73 / cm |
| Conduire | 59,7 / cm | 10,15 / cm | 1,64 / cm |
Demi couches de valeur
Tableau des demi-couches de valeur (en cm) pour différents matériaux à des énergies de photons de 100, 200 et 500 keV.
| Absorbeur | 100 keV | 200 keV | 500 keV |
| Air | 3555 cm | 4359 cm | 6189 cm |
| Eau | 4,15 cm | 5,1 cm | 7.15 cm |
| Carbone | 2,07 cm | 2,53 cm | 3,54 cm |
| Aluminium | 1,59 cm | 2,14 cm | 3,05 cm |
| Le fer | 0,26 cm | 0,64 cm | 1,06 cm |
| Cuivre | 0,18 cm | 0,53 cm | 0,95 cm |
| Conduire | 0,012 cm | 0,068 cm | 0,42 cm |
Validité de la loi exponentielle
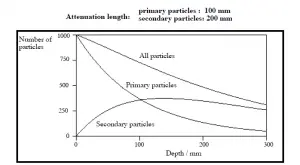
La loi exponentielle décrira toujours l’atténuation du rayonnement primaire par la matière. Si des particules secondaires sont produites ou si le rayonnement primaire change d’énergie ou de direction, alors l’atténuation effective sera bien moindre. Le rayonnement pénétrera plus profondément dans la matière que ne le prévoit la seule loi exponentielle. Le processus doit être pris en compte lors de l’évaluation de l’effet du blindage contre les radiations.
……………………………………………………………………………………………………………………………….
Cet article est basé sur la traduction automatique de l’article original en anglais. Pour plus d’informations, voir l’article en anglais. Pouvez vous nous aider Si vous souhaitez corriger la traduction, envoyez-la à l’adresse: [email protected] ou remplissez le formulaire de traduction en ligne. Nous apprécions votre aide, nous mettrons à jour la traduction le plus rapidement possible. Merci