Atténuation des rayons gamma
Voir aussi: Atténuation des rayons X
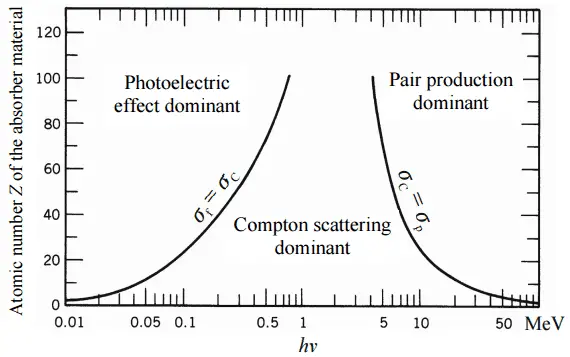
La section efficace totale d’interaction d’un rayonnement gamma avec un atome est égale à la somme des trois sections transversales partielles mentionnées: σ = σ f + σ C + σ p
- σ f – Effet photoélectrique
- σ C – Diffusion Compton
- σ p – Production de paires
Selon l’énergie des rayons gamma et le matériau absorbant, l’une des trois sections transversales partielles peut devenir beaucoup plus grande que les deux autres. Aux petites valeurs de l’énergie des rayons gamma, l’ effet photoélectrique domine. La diffusion de Compton domine aux énergies intermédiaires. La diffusion du compton augmente également avec la diminution du nombre atomique de matière, donc l’intervalle de domination est plus large pour les noyaux légers. Enfin, la production de paires électron-positon domine aux hautes énergies. Sur la base de la définition de la section efficace d’interaction, la dépendance de l’intensité des rayons gamma sur l’épaisseur du matériau absorbant peut être dérivée. Si les rayons gamma monoénergétiques sont collimatés en un faisceau étroitet si le détecteur derrière le matériau détecte uniquement les rayons gamma qui ont traversé ce matériau sans aucune sorte d’interaction avec ce matériau, alors la dépendance devrait être une simple atténuation exponentielle des rayons gamma . Chacune de ces interactions élimine le photon du faisceau soit par absorption, soit par diffusion loin de la direction du détecteur. Par conséquent, les interactions peuvent être caractérisées par une probabilité fixe d’occurrence par unité de longueur de trajet dans l’absorbeur. La somme de ces probabilités est appelée coefficient d’atténuation linéaire :
μ = τ (photoélectrique) + σ (Compton) + κ (paire)
Coefficient d’atténuation linéaire
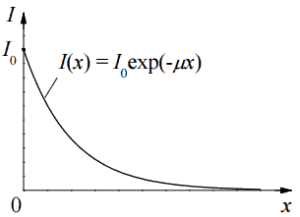
L’atténuation du rayonnement gamma peut alors être décrite par l’équation suivante.
I = I 0 .e -μx
, où I est l’intensité après atténuation, I o est l’intensité incidente, μ est le coefficient d’atténuation linéaire (cm -1 ) et l’épaisseur physique de l’absorbeur (cm).
Les matériaux énumérés dans le tableau ci-contre sont l’air, l’eau et différents éléments du carbone ( Z = 6) au plomb ( Z = 82) et leurs coefficients d’atténuation linéaire sont donnés pour trois énergies de rayons gamma. Il existe deux caractéristiques principales du coefficient d’atténuation linéaire:
- Le coefficient d’atténuation linéaire augmente à mesure que le numéro atomique de l’absorbeur augmente.
- Le coefficient d’atténuation linéaire pour tous les matériaux diminue avec l’énergie des rayons gamma.
Demi couche de valeur
![]() La couche à demi-valeur exprime l’épaisseur du matériau absorbant nécessaire pour réduire l’intensité du rayonnement incident d’un facteur deux . Il existe deux caractéristiques principales de la couche de demi-valeur:
La couche à demi-valeur exprime l’épaisseur du matériau absorbant nécessaire pour réduire l’intensité du rayonnement incident d’un facteur deux . Il existe deux caractéristiques principales de la couche de demi-valeur:
- La couche de demi-valeur diminue à mesure que le numéro atomique de l’absorbeur augmente. Par exemple, 35 m d’air sont nécessaires pour réduire l’intensité d’un faisceau de rayons gamma de 100 keV par un facteur de deux alors que seulement 0,12 mm de plomb peut faire la même chose.
- La couche de demi-valeur pour tous les matériaux augmente avec l’énergie des rayons gamma. Par exemple de 0,26 cm pour le fer à 100 keV à environ 1,06 cm à 500 keV.
Coefficient d’atténuation de masse
Lors de la caractérisation d’un matériau absorbant, on peut parfois utiliser le coefficient d’atténuation massique. Le coefficient d’atténuation massique est défini comme le rapport du coefficient d’atténuation linéaire et de la densité d’absorbeur (μ / ρ) . L’atténuation du rayonnement gamma peut alors être décrite par l’équation suivante:
I = I 0 .e – (μ / ρ) .ρl
, où ρ est la densité du matériau, (μ / ρ) est le coefficient d’atténuation de la masse et ρ.l est l’épaisseur de la masse. L’unité de mesure utilisée pour le coefficient d’atténuation de masse cm 2 g -1 .Pour les énergies intermédiaires, la diffusion Compton domine et différents absorbeurs ont des coefficients d’atténuation de masse approximativement égaux. Cela est dû au fait que la section efficace de la diffusion Compton est proportionnelle au Z (numéro atomique) et donc le coefficient est proportionnel à la densité du matériau ρ. Aux petites valeurs de l’énergie des rayons gamma ou aux valeurs élevées de l’énergie des rayons gamma, où le coefficient est proportionnel aux puissances supérieures du numéro atomique Z (pour l’effet photoélectrique σ f ~ Z 5 ; pour la production de paires σ p ~ Z2 ), le coefficient d’atténuation μ n’est pas une constante.
Exemple:
De quelle quantité d’eau absorbez-vous la chaleur si vous souhaitez réduire l’intensité d’un faisceau de rayons gamma monoénergétique de 500 keV ( faisceau étroit ) à 1% de son intensité incidente? La couche de demi-valeur pour les rayons gamma à 500 keV dans l’eau est de 7,15 cm et le coefficient d’atténuation linéaire pour les rayons gamma à 500 keV dans l’eau est de 0,097 cm -1 . La question est assez simple et peut être décrite par l’équation suivante:Si la couche de demi-valeur pour l’eau est de 7,15 cm, le coefficient d’atténuation linéaire est:
Maintenant, nous pouvons utiliser l’équation d’atténuation exponentielle:
donc
L’épaisseur d’eau requise est donc d’environ 47,5 cm . C’est une épaisseur relativement importante et elle est causée par de petits nombres atomiques d’hydrogène et d’oxygène. Si nous calculons le même problème pour le plomb (Pb) , nous obtenons l’épaisseur x = 2,8 cm .
Coefficients d’atténuation linéaire
Tableau des coefficients d’atténuation linéaire (en cm-1) pour différents matériaux à des énergies de rayons gamma de 100, 200 et 500 keV.
| Absorbeur | 100 keV | 200 keV | 500 keV |
| Air | 0,000195 / cm | 0,000159 / cm | 0,000112 / cm |
| Eau | 0,167 / cm | 0,136 / cm | 0,097 / cm |
| Carbone | 0,335 / cm | 0,274 / cm | 0,196 / cm |
| Aluminium | 0,435 / cm | 0,324 / cm | 0,227 / cm |
| Le fer | 2,72 / cm | 1,09 / cm | 0,655 / cm |
| Cuivre | 3,8 / cm | 1,309 / cm | 0,73 / cm |
| Conduire | 59,7 / cm | 10,15 / cm | 1,64 / cm |
Demi couches de valeur
Tableau des demi-couches de valeur (en cm) pour différents matériaux à des énergies de rayons gamma de 100, 200 et 500 keV.
| Absorbeur | 100 keV | 200 keV | 500 keV |
| Air | 3555 cm | 4359 cm | 6189 cm |
| Eau | 4,15 cm | 5,1 cm | 7.15 cm |
| Carbone | 2,07 cm | 2,53 cm | 3,54 cm |
| Aluminium | 1,59 cm | 2,14 cm | 3,05 cm |
| Le fer | 0,26 cm | 0,64 cm | 1,06 cm |
| Cuivre | 0,18 cm | 0,53 cm | 0,95 cm |
| Conduire | 0,012 cm | 0,068 cm | 0,42 cm |
Validité de la loi exponentielle
La loi exponentielle décrira toujours l’atténuation du rayonnement primaire par la matière. Si des particules secondaires sont produites ou si le rayonnement primaire change d’énergie ou de direction, alors l’atténuation effective sera bien moindre. Le rayonnement pénétrera plus profondément dans la matière que ne le prévoit la seule loi exponentielle. Le processus doit être pris en compte lors de l’évaluation de l’effet du blindage contre les radiations.
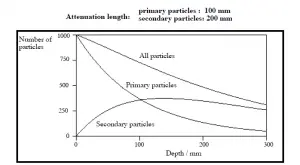
Facteurs d’accumulation pour le blindage des rayons gamma
Le facteur d’accumulation est un facteur de correction qui tient compte de l’influence du rayonnement diffusé et de toutes les particules secondaires dans le milieu lors des calculs de blindage. Si nous voulons tenir compte de l’accumulation de rayonnement secondaire, nous devons inclure le facteur d’accumulation . Le facteur d’accumulation est alors un facteur multiplicatif qui rend compte de la réponse aux photons non collidés de manière à inclure la contribution des photons diffusés. Ainsi, le facteur d’accumulation peut être obtenu en tant que rapport de la dose totale à la réponse pour la dose non prise.
Voir aussi: Blindage des rayons gamma
La formule étendue pour le calcul du débit de dose est la suivante:
La norme ANSI / ANS-6.4.3-1991 sur les coefficients d’atténuation des rayons gamma et les facteurs d’accumulation pour les matériaux d’ingénierie contient des coefficients d’atténuation des rayons gamma et des facteurs d’accumulation pour certains matériaux et éléments d’ingénierie à utiliser dans les calculs de blindage (ANSI / ANS-6.1 .1, 1991).
……………………………………………………………………………………………………………………………….
Cet article est basé sur la traduction automatique de l’article original en anglais. Pour plus d’informations, voir l’article en anglais. Pouvez vous nous aider Si vous souhaitez corriger la traduction, envoyez-la à l’adresse: [email protected] ou remplissez le formulaire de traduction en ligne. Nous apprécions votre aide, nous mettrons à jour la traduction le plus rapidement possible. Merci
