Dämpfung von Gammastrahlen
Siehe auch: Röntgendämpfung
Der Gesamtwechselwirkungsquerschnitt einer Gammastrahlung mit einem Atom ist gleich der Summe aller drei genannten Teilquerschnitte: σ = σ f + σ C + σ p
- σ f – Photoelektrischer Effekt
- σ C – Compton-Effekt
- σ p – Paarproduktion
In Abhängigkeit von der Gammastrahlenenergie und dem Absorbermaterial kann einer der drei Teilquerschnitte viel größer werden als die beiden anderen. Bei kleinen Werten der Gammastrahlenenergie dominiert der photoelektrische Effekt . Bei mittleren Energien dominiert die Compton-Effekt . Die Elektronenstreuung nimmt auch mit abnehmender Ordnungszahl der Materie zu, daher ist das Dominanzintervall für Lichtkerne breiter. Schließlich dominiert bei hohen Energien die Elektronen-Positronen-Paarbildung. Aus der Definition des Wechselwirkungsquerschnitts lässt sich die Abhängigkeit der Intensität der Gammastrahlen von der Dicke des Absorbermaterials ableiten. Wenn monoenergetische Gammastrahlen zu einem schmalen Strahl gebündelt werdenund wenn der Detektor hinter dem Material nur die Gammastrahlen erfasst, die durch dieses Material hindurchgegangen sind, ohne dass irgendeine Wechselwirkung mit diesem Material vorliegt, sollte die Abhängigkeit eine einfache exponentielle Dämpfung der Gammastrahlen sein . Bei jeder dieser Wechselwirkungen wird das Photon entweder durch Absorption oder durch Streuung von der Detektorrichtung aus dem Strahl entfernt. Daher können die Wechselwirkungen durch eine feste Auftrittswahrscheinlichkeit pro Weglängeneinheit im Absorber charakterisiert werden. Die Summe dieser Wahrscheinlichkeiten wird Absorptionskoeffizient genannt :
μ = τ (fotoelektrisch) + σ (Compton) + κ (Paar)
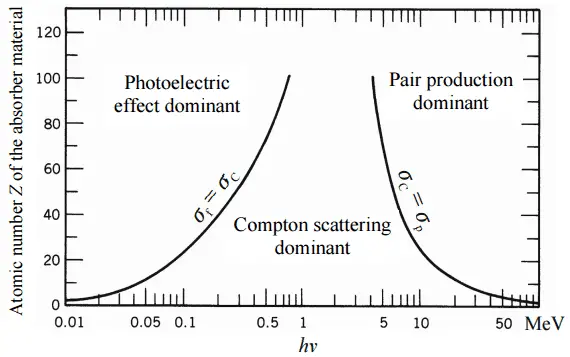
Absorptionskoeffizient
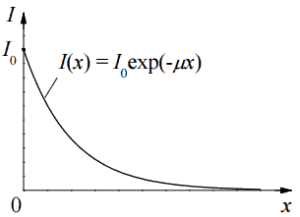
Die Dämpfung der Gammastrahlung kann dann durch die folgende Gleichung beschrieben werden.
I = I 0 .e -μx
wobei I die Intensität nach der Dämpfung ist, I o die Einfallsintensität ist, μ der lineare Dämpfungskoeffizient (cm –1 ) und die physikalische Dicke des Absorbers (cm) ist.
Die in der nebenstehenden Tabelle aufgeführten Materialien sind Luft, Wasser und verschiedene Elemente von Kohlenstoff ( Z = 6) bis Blei ( Z = 82). Ihre linearen Dämpfungskoeffizienten sind für drei Gammastrahlenenergien angegeben. Es gibt zwei Hauptmerkmale des linearen Dämpfungskoeffizienten:
- Der lineare Dämpfungskoeffizient nimmt mit zunehmender Ordnungszahl des Absorbers zu.
- Der lineare Dämpfungskoeffizient für alle Materialien nimmt mit der Energie der Gammastrahlen ab.
Halbe Wertebene
![]() Die Halbwertsschicht drückt die Dicke des absorbierenden Materials aus, die zur Verringerung der Intensität der einfallenden Strahlung um den Faktor zwei benötigt wird . Es gibt zwei Hauptmerkmale der Halbwertsschicht:
Die Halbwertsschicht drückt die Dicke des absorbierenden Materials aus, die zur Verringerung der Intensität der einfallenden Strahlung um den Faktor zwei benötigt wird . Es gibt zwei Hauptmerkmale der Halbwertsschicht:
- Die Halbwertsschicht nimmt mit zunehmender Ordnungszahl des Absorbers ab. Zum Beispiel werden 35 m Luft benötigt, um die Intensität eines 100-keV-Gammastrahls um den Faktor zwei zu verringern, während nur 0,12 mm Blei dasselbe bewirken können.
- Die Halbwertsschicht für alle Materialien nimmt mit der Energie der Gammastrahlen zu. Zum Beispiel von 0,26 cm für Eisen bei 100 keV bis etwa 1,06 cm bei 500 keV.
Massendämpfungskoeffizient
Bei der Charakterisierung eines absorbierenden Materials können wir manchmal den Massendämpfungskoeffizienten verwenden. Der Massendämpfungskoeffizient ist definiert als das Verhältnis des linearen Dämpfungskoeffizienten und der Absorberdichte (μ / ρ) . Die Dämpfung der Gammastrahlung kann dann durch die folgende Gleichung beschrieben werden:
I = I 0 .e – (μ / ρ) .ρl
wobei ρ die Materialdichte ist, (μ / ρ) der Massendämpfungskoeffizient ist und ρ.l die Massendicke ist. Die für den Massendämpfungskoeffizienten cm 2 g -1 verwendete Maßeinheit. Für Zwischenenergien dominiert die Compton-Effekt und verschiedene Absorber haben ungefähr gleiche Massendämpfungskoeffizienten. Dies liegt an der Tatsache, dass der Querschnitt der Compton-Effekt proportional zum Z (Ordnungszahl) ist und daher der Koeffizient proportional zur Materialdichte ρ ist. Bei kleinen Werten der Gammastrahlenenergie oder bei hohen Werten der Gammastrahlenenergie, wobei der Koeffizient proportional zu höheren Potenzen der Ordnungszahl Z ist (für den photoelektrischen Effekt σ f ~ Z 5 ; für die Paarproduktion σ p ~ Z.2 ) ist der Dämpfungskoeffizient μ keine Konstante.
Beispiel:
Wie viel Wasserschutz benötigen Sie, wenn Sie die Intensität eines monoenergetischen 500-keV- Gammastrahls ( schmaler Strahl ) auf 1% seiner Einfallsintensität reduzieren möchten ? Die Halbwertsschicht für 500 keV Gammastrahlen in Wasser beträgt 7,15 cm und der lineare Dämpfungskoeffizient für 500 keV Gammastrahlen in Wasser beträgt 0,097 cm -1 . Die Frage ist recht einfach und kann durch folgende Gleichung beschrieben werden:Wenn die Halbwertsschicht für Wasser 7,15 cm beträgt, beträgt der lineare Dämpfungskoeffizient:
Jetzt können wir die exponentielle Dämpfungsgleichung verwenden:
deshalb
Die erforderliche Wasserdicke beträgt also ca. 47,5 cm . Dies ist eine relativ große Dicke und wird durch kleine Atomzahlen von Wasserstoff und Sauerstoff verursacht. Wenn wir das gleiche Problem für Blei (Pb) berechnen , erhalten wir die Dicke x = 2,8 cm .
Lineare Dämpfungskoeffizienten
Tabelle der linearen Dämpfungskoeffizienten (in cm & supmin ; ¹ ) für verschiedene Materialien bei Gammastrahlenenergien von 100, 200 und 500 keV.
| Absorber | 100 keV | 200 keV | 500 keV |
| Luft | 0,000195 / cm | 0,000159 / cm | 0,000112 / cm |
| Wasser | 0,167 / cm | 0,136 / cm | 0,097 / cm |
| Kohlenstoff | 0,335 / cm | 0,274 / cm | 0,196 / cm |
| Aluminium | 0,435 / cm | 0,324 / cm | 0,227 / cm |
| Eisen | 2,72 / cm | 1,09 / cm | 0,655 / cm |
| Kupfer | 3,8 / cm | 1,309 / cm | 0,73 / cm |
| Führen | 59,7 / cm | 10,15 / cm | 1,64 / cm |
Halbe Wertebenen
Tabelle der Halbwertsschichten (in cm) für verschiedene Materialien bei Gammastrahlenenergien von 100, 200 und 500 keV.
| Absorber | 100 keV | 200 keV | 500 keV |
| Luft | 3555 cm | 4359 cm | 6189 cm |
| Wasser | 4,15 cm | 5,1 cm | 7,15 cm |
| Kohlenstoff | 2,07 cm | 2,53 cm | 3,54 cm |
| Aluminium | 1,59 cm | 2,14 cm | 3,05 cm |
| Eisen | 0,26 cm | 0,64 cm | 1,06 cm |
| Kupfer | 0,18 cm | 0,53 cm | 0,95 cm |
| Führen | 0,012 cm | 0,068 cm | 0,42 cm |
Gültigkeit des Exponentialgesetzes
Das Exponentialgesetz beschreibt immer die Dämpfung der Primärstrahlung durch Materie. Wenn Sekundärteilchen erzeugt werden oder wenn die Primärstrahlung ihre Energie oder Richtung ändert, ist die effektive Dämpfung viel geringer. Die Strahlung dringt tiefer in die Materie ein, als es das Exponentialgesetz allein vorschreibt. Der Prozess muss bei der Bewertung der Wirkung der Strahlenabschirmung berücksichtigt werden.
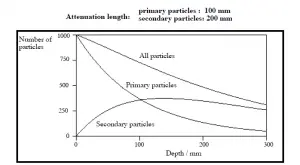
Aufbaufaktoren für die Abschirmung von Gammastrahlen
Der Aufbaufaktor ist ein Korrekturfaktor, der den Einfluss der gestreuten Strahlung plus aller Sekundärteilchen im Medium bei Abschirmungsberechnungen berücksichtigt. Wenn wir den Aufbau von Sekundärstrahlung berücksichtigen wollen, müssen wir den Aufbaufaktor einbeziehen . Der Aufbaufaktor ist dann ein multiplikativer Faktor, der die Reaktion auf die nicht kollidierten Photonen berücksichtigt, um den Beitrag der gestreuten Photonen einzuschließen. Somit kann der Aufbaufaktor als Verhältnis der Gesamtdosis zur Reaktion auf die nicht kollidierte Dosis erhalten werden.
Siehe auch: Gammastrahlenabschirmung
Die erweiterte Formel für die Berechnung der Dosisleistung lautet:
Der ANSI / ANS-6.4.3-1991-Gammastrahlen-Dämpfungskoeffizienten und Aufbaufaktoren für technische Materialien enthält abgeleitete Gammastrahlen-Dämpfungskoeffizienten und Aufbaufaktoren für ausgewählte technische Materialien und Elemente zur Verwendung bei Abschirmungsberechnungen (ANSI / ANS-6.1) .1, 1991).
……………………………………………………………………………………………………………………………….
Dieser Artikel basiert auf der maschinellen Übersetzung des englischen Originalartikels. Weitere Informationen finden Sie im Artikel auf Englisch. Sie können uns helfen. Wenn Sie die Übersetzung korrigieren möchten, senden Sie diese bitte an: [email protected] oder füllen Sie das Online-Übersetzungsformular aus. Wir bedanken uns für Ihre Hilfe und werden die Übersetzung so schnell wie möglich aktualisieren. Danke.
